What Is 15 Of 2500
gasmanvison
Sep 20, 2025 · 5 min read
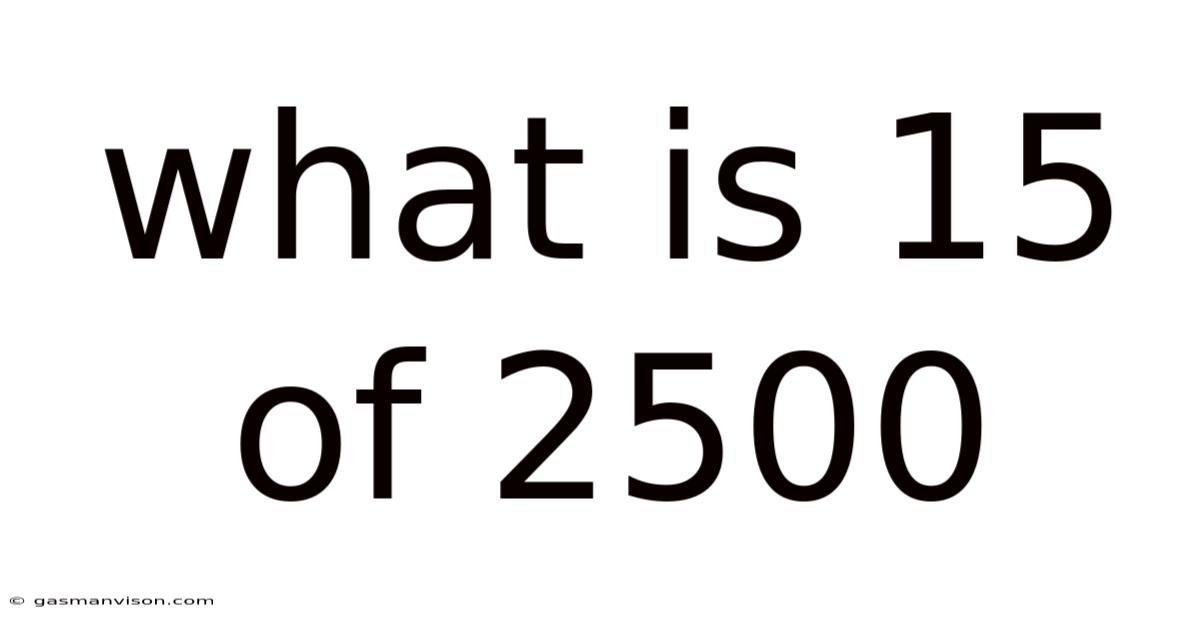
Table of Contents
What is 15% of 2500? A Deep Dive into Percentages and Their Applications
Finding 15% of 2500 might seem like a simple arithmetic problem, solvable with a quick calculator search. But understanding the underlying concepts of percentages and their diverse applications offers a far richer understanding. This article will not only answer the question directly but will explore the various methods for calculating percentages, the importance of percentage calculations in everyday life, and delve into more complex scenarios involving percentages.
Meta Description: Learn how to calculate 15% of 2500 and understand the broader applications of percentages in various fields, from finance to statistics. This comprehensive guide explores different calculation methods and real-world examples.
Calculating 15% of 2500: The Basic Approach
The most straightforward method involves converting the percentage to a decimal and multiplying it by the whole number. Fifteen percent (15%) can be expressed as 0.15 (15 divided by 100). Therefore, to find 15% of 2500, we perform the following calculation:
0.15 * 2500 = 375
Therefore, 15% of 2500 is 375. This is the fundamental approach, easily adaptable for calculating any percentage of any number.
Alternative Calculation Methods
While the decimal method is the most common and efficient, several other methods exist, each offering a different perspective on percentage calculation:
-
Fraction Method: 15% can be represented as the fraction 15/100. To find 15% of 2500, we can perform the calculation: (15/100) * 2500. This simplifies to (3/20) * 2500, which, after canceling out common factors, leads to the same result: 375. This method is particularly useful when dealing with simpler percentages that can be easily converted into fractions.
-
Proportion Method: This method sets up a proportion to solve for the unknown value. We can express the problem as: 15/100 = x/2500, where 'x' represents 15% of 2500. Cross-multiplying and solving for 'x' will yield the same answer: x = 375. This method provides a structured approach, particularly helpful in solving more complex percentage problems.
-
Using a Calculator: Most calculators have a percentage function (%) that simplifies the calculation. Inputting 2500 * 15% directly into the calculator will give the answer 375. This method is the quickest and most convenient for everyday use.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in many real-world scenarios:
-
Finance: Percentages are fundamental in finance, used extensively in calculating interest rates, loan payments, discounts, taxes, investment returns, and profit margins. For example, if a bank offers a 5% interest rate on a savings account, knowing how to calculate percentages helps you determine the exact amount of interest earned. Similarly, calculating the sales tax on a purchase or the discount on a sale item involves percentage calculations.
-
Statistics: Percentages are essential for interpreting statistical data. Representing data as percentages allows for easier comparison and understanding of proportions. For example, understanding that 75% of respondents to a survey prefer a certain product provides a clear picture of consumer preference.
-
Science: In scientific fields, percentages are used to express concentrations, error rates, and changes in measurements. For example, expressing the concentration of a solution as a percentage or indicating the percentage error in an experiment utilizes percentage calculations.
-
Retail and Business: Businesses rely heavily on percentage calculations for pricing strategies, profit margins, sales analysis, and inventory management. Understanding markups, discounts, and sales tax is critical for successful business operations. Analyzing sales figures to see the percentage increase or decrease in sales from one period to another is essential for business planning.
-
Everyday Life: From calculating tips at restaurants (e.g., calculating a 15% tip on a meal bill) to understanding discounts in stores (e.g., a 20% off sale), percentages are ubiquitous in our daily lives. Understanding percentage calculations empowers you to make informed decisions and manage your finances effectively.
Beyond the Basics: More Complex Percentage Problems
While finding 15% of 2500 is a straightforward calculation, more complex scenarios frequently involve multiple percentage changes or finding the original value after a percentage increase or decrease.
Scenario 1: Successive Percentage Changes:
Imagine a product initially priced at 2500 undergoes two successive price reductions: a 10% discount followed by a further 5% discount. These discounts are not additive; they are applied sequentially.
-
Step 1: Calculate the 10% discount: 0.10 * 2500 = 250. The price after the first discount is 2500 - 250 = 2250.
-
Step 2: Calculate the 5% discount on the reduced price: 0.05 * 2250 = 112.50. The final price after both discounts is 2250 - 112.50 = 2137.50.
This example demonstrates that successive percentage changes do not simply add up; the second percentage is applied to the already reduced value.
Scenario 2: Finding the Original Value After a Percentage Increase:
Let's say the price of a commodity increased by 15% to reach 2500. To find the original price, we need to work backward. The final price (2500) represents 115% (100% + 15%) of the original price.
We can set up the equation: 1.15 * x = 2500, where 'x' is the original price. Solving for 'x', we get x = 2500 / 1.15 ≈ 2173.91. The original price was approximately 2173.91.
Scenario 3: Percentage Increase or Decrease Calculation:
Calculating the percentage increase or decrease between two values is also common. Let's say the sales increased from 2000 to 2500. To calculate the percentage increase:
-
Step 1: Find the difference: 2500 - 2000 = 500
-
Step 2: Divide the difference by the original value: 500 / 2000 = 0.25
-
Step 3: Multiply by 100 to express it as a percentage: 0.25 * 100 = 25%
Therefore, the sales increased by 25%. The same principle applies to calculating percentage decreases.
Conclusion: Mastering Percentages for a Data-Driven World
The seemingly simple question, "What is 15% of 2500?", opens a door to a vast world of percentage applications. Understanding the various methods for calculating percentages and their real-world applications is crucial for success in various fields. From personal finance to complex statistical analysis, mastering percentage calculations equips you with the skills to navigate a data-driven world effectively and make informed decisions based on numerical data. By understanding the concepts explored in this article, you can confidently tackle various percentage problems and apply this knowledge to numerous aspects of your personal and professional life. Remember to practice regularly and apply these methods to real-world scenarios to solidify your understanding. The more you practice, the more comfortable you'll become with these crucial mathematical concepts.
Latest Posts
Latest Posts
-
1 3 3 5 Fraction
Sep 20, 2025
-
Professional Signs And Lettering Error
Sep 20, 2025
-
What Is Wyldstyle Real Name
Sep 20, 2025
-
How Long Is An Eon
Sep 20, 2025
-
Is 1 4 Smaller Than 1 8
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 2500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.