What Is 2/3 Of 8
gasmanvison
Sep 23, 2025 · 5 min read
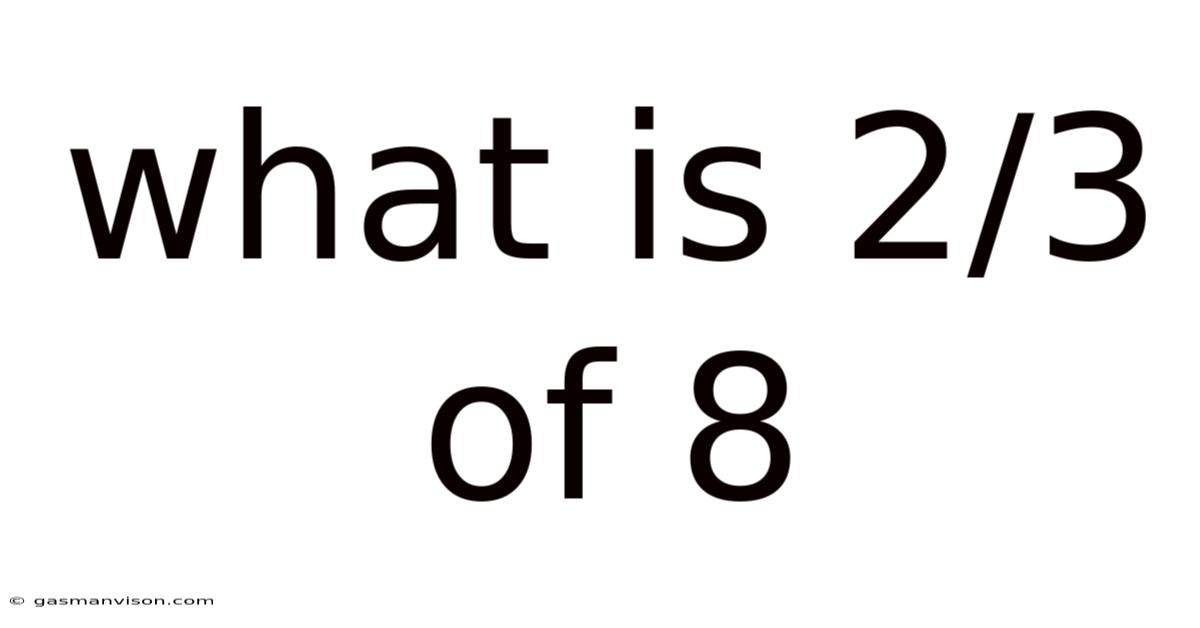
Table of Contents
What is 2/3 of 8? A Deep Dive into Fractions and Their Applications
This seemingly simple question, "What is 2/3 of 8?", opens the door to a fascinating exploration of fractions, their practical applications, and the fundamental principles of mathematics. While the answer itself is easily calculated, understanding the underlying concepts is crucial for mastering more complex mathematical problems and real-world scenarios. This article will not only provide the answer but also delve into the various methods of solving this problem, exploring different approaches and their relevance to broader mathematical concepts. We'll also examine the practical applications of fractional calculations in everyday life.
Meta Description: Learn how to calculate 2/3 of 8 and explore the world of fractions. This comprehensive guide covers multiple methods, real-world applications, and expands on fundamental mathematical principles.
Understanding Fractions: A Quick Refresher
Before diving into the calculation, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, and the denominator indicates the total number of equal parts the whole is divided into. In our example, 2/3, the numerator is 2, and the denominator is 3. This means we are looking for two out of three equal parts.
Method 1: Direct Multiplication
The most straightforward method to find 2/3 of 8 is to multiply the fraction by the whole number. We can express 8 as a fraction, 8/1. Therefore, the calculation becomes:
(2/3) * (8/1) = (2 * 8) / (3 * 1) = 16/3
This results in an improper fraction, meaning the numerator is larger than the denominator. To convert it into a mixed number (a whole number and a fraction), we perform division:
16 ÷ 3 = 5 with a remainder of 1.
Therefore, 16/3 is equal to 5 1/3.
This method is efficient and clearly demonstrates the fundamental principle of multiplying fractions.
Method 2: Finding One-Third, Then Doubling
Instead of direct multiplication, we can break down the problem into smaller, more manageable steps. First, we find one-third of 8:
8 ÷ 3 = 8/3 = 2 2/3
Since we need two-thirds, we simply multiply this result by 2:
(8/3) * 2 = 16/3 = 5 1/3
This method is particularly useful for mental calculations or when dealing with larger numbers. It breaks down a complex calculation into simpler steps, making it easier to understand and follow.
Method 3: Using Decimals
Converting fractions to decimals can also provide a solution. We convert 2/3 to a decimal by dividing the numerator by the denominator:
2 ÷ 3 ≈ 0.6667 (This is a recurring decimal)
Then, we multiply this decimal by 8:
0.6667 * 8 ≈ 5.3336
Rounding to the nearest third, we get 5 1/3. While this method utilizes decimals, the result aligns with the previous methods, highlighting the consistency of mathematical principles. It's important to note that using decimals introduces a slight approximation due to the recurring nature of the decimal representation of 2/3.
Real-World Applications: Where Fractions Matter
The seemingly simple calculation of 2/3 of 8 has numerous real-world applications across various fields:
- Cooking and Baking: Recipes often require fractional amounts of ingredients. Understanding fractions is crucial for accurately measuring ingredients and ensuring consistent results. For instance, a recipe might call for 2/3 of a cup of sugar.
- Construction and Engineering: Precise measurements are paramount in construction and engineering. Fractions are used extensively in blueprints, calculations, and material estimations. A carpenter might need to cut a piece of wood to 2/3 of its length.
- Finance and Economics: Fractions are ubiquitous in finance, from calculating interest rates and stock prices to understanding percentages and ratios. For example, understanding fractional shares allows for more granular investment strategies.
- Data Analysis and Statistics: Fractions are integral to statistical analysis, data representation, and probability calculations. Understanding fractions allows for precise interpretation of data and trends.
- Everyday Life: From sharing pizza slices to calculating discounts, fractions are constantly present in our daily lives.
Expanding the Concept: Working with More Complex Fractions
Understanding the calculation of 2/3 of 8 provides a foundation for tackling more complex fraction problems. Consider these extensions:
- Fractions with larger numbers: Applying the same methods to larger numbers reinforces the understanding of the principles involved.
- Mixed numbers: Working with mixed numbers (a whole number and a fraction) requires an additional step of converting them to improper fractions before performing calculations.
- Operations with multiple fractions: Problems involving addition, subtraction, multiplication, and division of fractions require a thorough grasp of fraction operations.
- Solving for unknowns: Problems where one of the components (fraction, whole number, or the result) is unknown require algebraic manipulation to find the solution.
Importance of Mastering Fractions: A Stepping Stone to Higher Mathematics
Proficiency in fractions is not merely about solving simple problems; it is a crucial building block for more advanced mathematical concepts. Fractions are fundamental to:
- Algebra: Understanding fractions is essential for working with algebraic expressions, equations, and inequalities.
- Calculus: Calculus relies heavily on the principles of limits, derivatives, and integrals, all of which are built upon a solid foundation in fractions and rational numbers.
- Geometry: Many geometric calculations, particularly those involving ratios and proportions, utilize fractions.
Conclusion: Beyond the Answer
While the answer to "What is 2/3 of 8?" is 5 1/3, the true value of this question lies in the journey of understanding the underlying concepts. Mastering fractions is not just about memorizing formulas; it's about developing a deep understanding of their meaning, their applications, and their role as a cornerstone of mathematics. The methods explored in this article provide a solid foundation for tackling more complex mathematical problems and real-world scenarios. By understanding these principles, one gains a valuable skill applicable in numerous aspects of life, from everyday tasks to advanced academic pursuits. The seemingly simple question unveils a world of mathematical possibilities, illustrating the power and elegance of fractions.
Latest Posts
Latest Posts
-
Half Of 1 2 3 Cup
Sep 23, 2025
-
43 Degrees F To C
Sep 23, 2025
-
2 6 Is Equivalent To
Sep 23, 2025
-
Which Scenario Demonstrates Project Landing
Sep 23, 2025
-
What Equals 18 In Multiplication
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.