What Is 2/5 Equivalent To
gasmanvison
Sep 15, 2025 · 5 min read
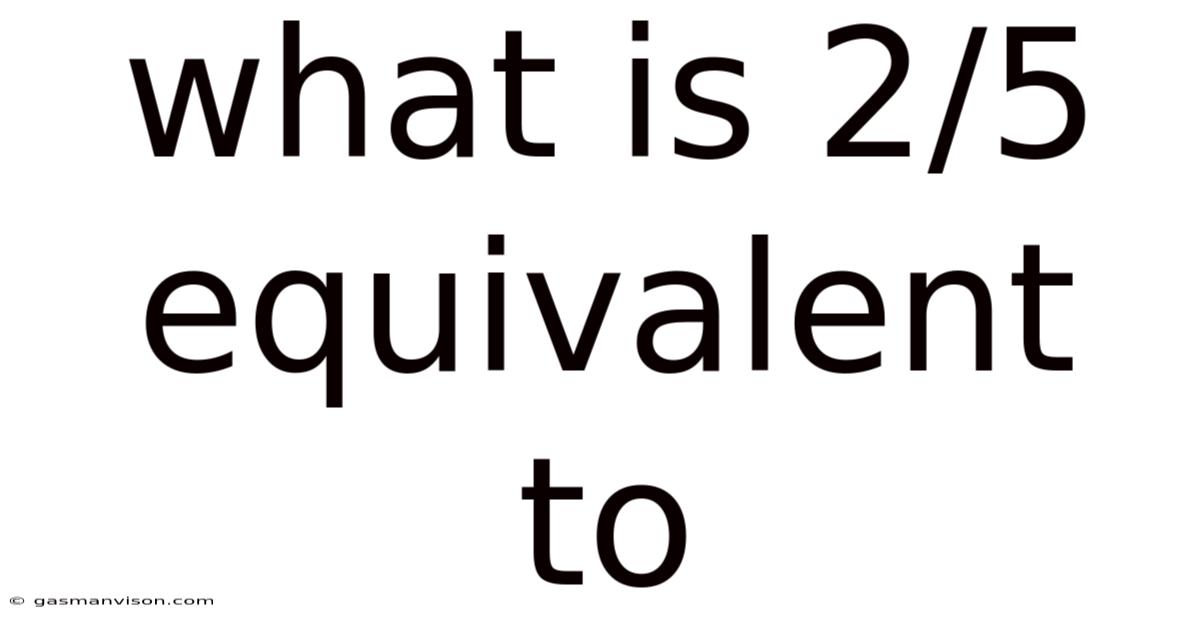
Table of Contents
What is 2/5 Equivalent To? A Deep Dive into Fraction Equivalence
This article explores the concept of fraction equivalence, focusing specifically on the fraction 2/5. We'll delve into various methods for finding equivalent fractions, their applications in real-world scenarios, and explore the broader mathematical concepts behind them. Understanding equivalent fractions is crucial for mastering fundamental arithmetic, algebra, and even more advanced mathematical concepts. This comprehensive guide will equip you with a robust understanding of 2/5 and its equivalents.
Understanding Fractions: A Quick Recap
Before we dive into the equivalence of 2/5, let's briefly review the fundamental components of a fraction. A fraction represents a part of a whole. It consists of two main parts:
- Numerator: The top number indicates how many parts we have. In the fraction 2/5, the numerator is 2.
- Denominator: The bottom number indicates the total number of equal parts the whole is divided into. In the fraction 2/5, the denominator is 5.
Therefore, 2/5 represents 2 parts out of a total of 5 equal parts.
Finding Equivalent Fractions for 2/5
The key to finding equivalent fractions lies in the concept of multiplying or dividing both the numerator and the denominator by the same non-zero number. This process maintains the proportional relationship between the numerator and the denominator, thus resulting in a fraction that represents the same value.
Let's illustrate this with 2/5:
- Multiplying by 2: (2 x 2) / (5 x 2) = 4/10. Therefore, 4/10 is equivalent to 2/5.
- Multiplying by 3: (2 x 3) / (5 x 3) = 6/15. Similarly, 6/15 is equivalent to 2/5.
- Multiplying by 4: (2 x 4) / (5 x 4) = 8/20. Again, 8/20 is equivalent to 2/5.
We can continue this process indefinitely, generating an infinite number of equivalent fractions for 2/5. Each fraction represents the same proportion, or the same point on the number line.
Dividing (Simplifying) Fractions
Conversely, we can also simplify fractions by dividing both the numerator and the denominator by the same non-zero number. This process is also known as reducing the fraction to its simplest form. While 2/5 is already in its simplest form (because 2 and 5 share no common factors other than 1), let's illustrate with an example:
Consider the fraction 10/25. Both the numerator (10) and the denominator (25) are divisible by 5:
(10 ÷ 5) / (25 ÷ 5) = 2/5
Therefore, 10/25 simplifies to 2/5, confirming that they are equivalent fractions.
Visual Representation of Equivalent Fractions
Visualizing equivalent fractions can significantly enhance understanding. Imagine a pizza cut into 5 equal slices. If you eat 2 slices, you've eaten 2/5 of the pizza. Now, imagine the same pizza cut into 10 equal slices. If you eat 4 of these smaller slices, you've still eaten the same amount – 4/10, which is equivalent to 2/5. This visual representation clearly demonstrates the equivalence. The same principle applies to any other visual representation, like dividing a rectangle into equal parts.
Real-World Applications of Equivalent Fractions
Understanding equivalent fractions is crucial in numerous real-world applications:
- Cooking and Baking: Recipes often require adjustments. If a recipe calls for 2/5 of a cup of flour, you can easily find an equivalent fraction like 4/10 or 6/15, allowing you to use different measuring tools.
- Construction and Measurement: Measuring lengths and areas often involves working with fractions. Equivalent fractions ensure accuracy and consistency in measurements.
- Financial Calculations: Understanding percentages and proportions involves working with fractions and their equivalents. For instance, expressing a discount of 40% can also be represented as 2/5.
- Data Analysis: Representing data visually through charts and graphs often involves using fractions and proportions, requiring the understanding and manipulation of equivalent fractions.
Decimals and Percentages: Another Perspective on 2/5
Equivalent fractions can also be expressed as decimals and percentages. To convert a fraction to a decimal, divide the numerator by the denominator:
2 ÷ 5 = 0.4
Therefore, 2/5 is equivalent to 0.4.
To convert a decimal to a percentage, multiply by 100:
0.4 x 100 = 40%
Hence, 2/5 is also equivalent to 40%.
This demonstrates the interconnectedness of fractions, decimals, and percentages, highlighting the versatility of understanding equivalent fractions.
Advanced Concepts and Applications
The concept of equivalent fractions extends beyond basic arithmetic. It plays a crucial role in:
- Algebra: Solving equations involving fractions often requires finding common denominators, which is directly related to the concept of equivalent fractions.
- Calculus: Understanding limits and derivatives involves working with infinitesimal changes, often expressed using fractions and their equivalents.
- Probability: Calculating probabilities often involves working with fractions, where understanding equivalent fractions is essential for simplifying and interpreting results.
- Geometry: Working with ratios and proportions in geometric problems relies heavily on the understanding of equivalent fractions.
Addressing Common Mistakes and Misconceptions
A common mistake is incorrectly adding or subtracting fractions with different denominators without first finding equivalent fractions with a common denominator. For example, adding 2/5 and 1/3 requires converting them to fractions with a common denominator (15 in this case): 6/15 + 5/15 = 11/15.
Another common misunderstanding is assuming that only multiplication and division create equivalent fractions. While true for maintaining equality, finding a common denominator for addition and subtraction involves implicit multiplication and division.
Conclusion: The Enduring Importance of Fraction Equivalence
Understanding equivalent fractions, particularly how to find equivalents for a fraction like 2/5, is a fundamental skill with far-reaching implications. From everyday tasks like cooking to advanced mathematical concepts, the ability to manipulate and interpret equivalent fractions is essential. This comprehensive guide has explored various methods, applications, and underlying mathematical concepts, equipping you with a strong foundation for tackling fraction-related problems with confidence. Mastering equivalent fractions not only simplifies arithmetic but also opens doors to a deeper understanding of more complex mathematical areas. Remember the core principle: multiplying or dividing both the numerator and denominator by the same non-zero number yields an equivalent fraction, maintaining the proportional relationship and representing the same value.
Latest Posts
Latest Posts
-
What Is A Genre Painting
Sep 15, 2025
-
Make Sure That Your Pet
Sep 15, 2025
-
What Times What Equals 20
Sep 15, 2025
-
Does Erosion Make A Sound
Sep 15, 2025
-
Who Was The Heaviest President
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/5 Equivalent To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.