What Is 20 Of 14
gasmanvison
Sep 06, 2025 · 5 min read
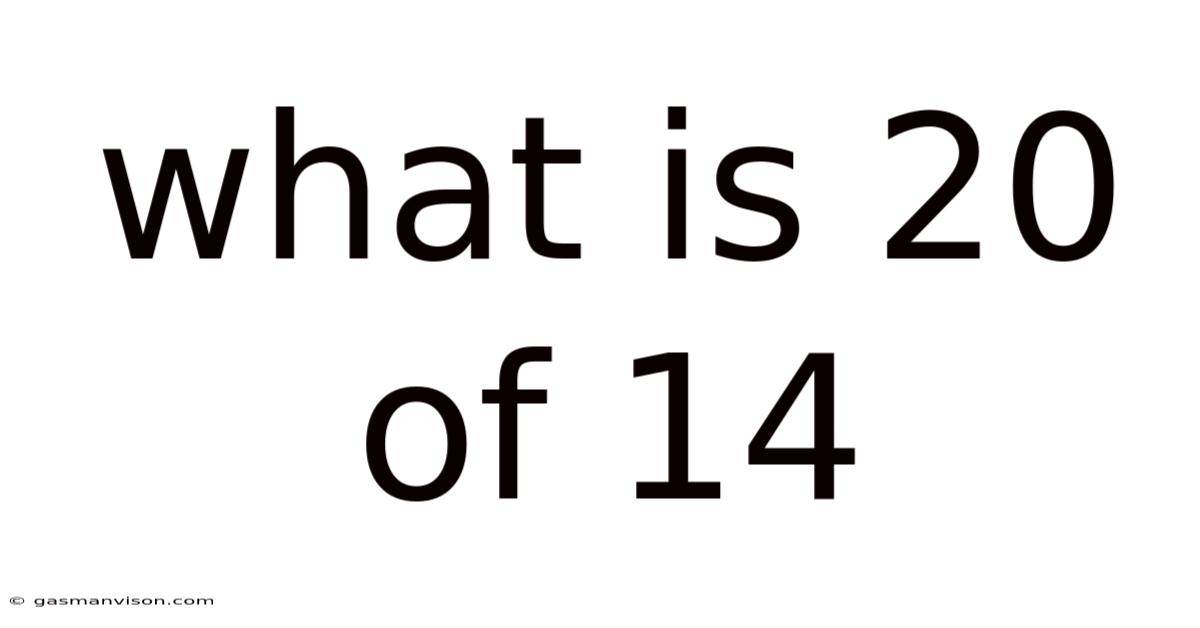
Table of Contents
What is 20% of 14? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 20% of 14?", opens a door to a vast world of mathematical concepts and practical applications. Understanding percentages is crucial in numerous fields, from everyday budgeting and shopping to complex financial analysis and scientific research. This article will not only answer the initial question but also explore the underlying principles of percentage calculations, delve into various methods of solving percentage problems, and showcase the real-world significance of this fundamental mathematical skill.
Meta Description: Learn how to calculate 20% of 14 and master percentage calculations. This comprehensive guide covers various methods, real-world applications, and the importance of understanding percentages.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" (from the Latin per centum). Therefore, 20% represents 20 parts out of 100, or 20/100, which can be simplified to 1/5.
This fractional representation is key to understanding percentage calculations. To find a percentage of a number, we essentially perform a multiplication operation. The formula is:
(Percentage/100) * Number = Result
In our specific case, we want to find 20% of 14. Substituting the values into the formula:
(20/100) * 14 = Result
This simplifies to:
(1/5) * 14 = 2.8
Therefore, 20% of 14 is 2.8.
Multiple Methods for Calculating Percentages
While the formula above is straightforward, several other methods can be used to calculate percentages, each with its own advantages and disadvantages. Let's explore some of them:
1. Using a Calculator: The simplest method is using a calculator. Most calculators have a percentage key (%) that directly performs the calculation. Simply enter 20%, press the multiplication key (*), enter 14, and press the equals key (=). The calculator will automatically provide the answer: 2.8.
2. Converting to Decimal: Percentages can be easily converted to decimals by dividing by 100. 20% becomes 0.20 (or simply 0.2). Multiplying this decimal by the number gives the result: 0.2 * 14 = 2.8. This method is particularly useful when working with more complex percentage calculations or using spreadsheets.
3. Proportions: Setting up a proportion can be a helpful visual approach, especially for beginners. We can set up a proportion as follows:
20/100 = x/14
Solving for 'x' (which represents 20% of 14) involves cross-multiplication:
20 * 14 = 100 * x
280 = 100x
x = 280/100 = 2.8
This method is more intuitive for those who prefer a visual representation of the problem.
4. Mental Math (for simpler percentages): For certain percentages like 10%, 20%, 25%, 50%, and others, mental math can be employed. For instance, 10% of a number is simply that number divided by 10. Therefore, 10% of 14 is 1.4. Since 20% is double 10%, we can double 1.4 to get 2.8. This approach is efficient for quick estimations.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a critical life skill applicable across various domains:
1. Finance and Budgeting: Percentages are fundamental in personal finance. Calculating interest rates on loans, savings accounts, and credit cards involves percentages. Understanding sales tax, discounts, tips, and investment returns all require proficient percentage calculations. Budgeting effectively also requires analyzing spending habits as percentages of total income.
2. Sales and Marketing: Businesses heavily rely on percentages for pricing strategies, sales promotions, and performance analysis. Discounts are usually expressed as percentages, and conversion rates (e.g., the percentage of website visitors who make a purchase) are crucial metrics for marketing effectiveness. Profit margins and return on investment (ROI) are also calculated as percentages.
3. Science and Statistics: Percentages play a vital role in data analysis and interpretation. Scientific experiments often present results as percentages, such as the percentage of participants who responded positively to a treatment. Statistical analyses frequently use percentages to represent proportions and probabilities. For example, calculating the percentage of a population with a specific characteristic or the probability of an event occurring is dependent on percentage calculations.
4. Everyday Life: Even seemingly mundane activities involve percentages. Calculating the percentage of a discount at a store, determining the tip amount at a restaurant, or understanding the nutritional information on food labels (e.g., percentage of daily recommended value for various nutrients) all demonstrate the practical application of percentages in daily life.
Advanced Percentage Calculations: Beyond the Basics
While finding 20% of 14 is a relatively simple task, understanding percentage calculations extends to more complex scenarios:
1. Finding the Percentage Increase or Decrease: This involves calculating the percentage change between two numbers. For example, if a product's price increased from $10 to $12, the percentage increase is calculated as:
((12 - 10) / 10) * 100% = 20%
2. Finding the Original Amount: If you know the percentage and the final amount after a percentage increase or decrease, you can calculate the original amount. This frequently arises in sales scenarios where the discounted price is known but the original price needs to be determined.
3. Compound Interest: Compound interest calculations, crucial in finance and investments, involve repeated applications of percentage calculations over time. The interest earned in one period is added to the principal amount, and the interest for the next period is calculated based on this new total.
4. Percentage Points vs. Percentage Change: It's crucial to distinguish between percentage points and percentage change. A change from 10% to 20% is a 10 percentage point increase, but it represents a 100% percentage change (because the initial value doubled). This distinction is critical for accurate interpretation of data.
Conclusion: The Enduring Importance of Percentages
The ability to calculate percentages is a fundamental mathematical skill with far-reaching applications. From everyday budgeting to complex financial modeling, understanding percentages is essential for navigating the numerical world. Mastering various methods for calculating percentages, appreciating their real-world applications, and understanding the nuances of advanced percentage calculations equips individuals with a powerful tool for problem-solving and decision-making in numerous contexts. Even the seemingly simple question of "What is 20% of 14?" reveals a depth of mathematical concepts that underpin our understanding and interaction with the world around us. The answer, 2.8, is merely the starting point of a much broader and more significant exploration.
Latest Posts
Latest Posts
-
Opposite Of Lazy In Spanish
Sep 06, 2025
-
G Ml To Lb Ft3
Sep 06, 2025
-
Which Statement Describes Heterogeneous Mixtures
Sep 06, 2025
-
How Many Pounds In 120kg
Sep 06, 2025
-
Iron Iii Sulfide Chemical Formula
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.