What Is 20 Of 25.00
gasmanvison
Sep 25, 2025 · 4 min read
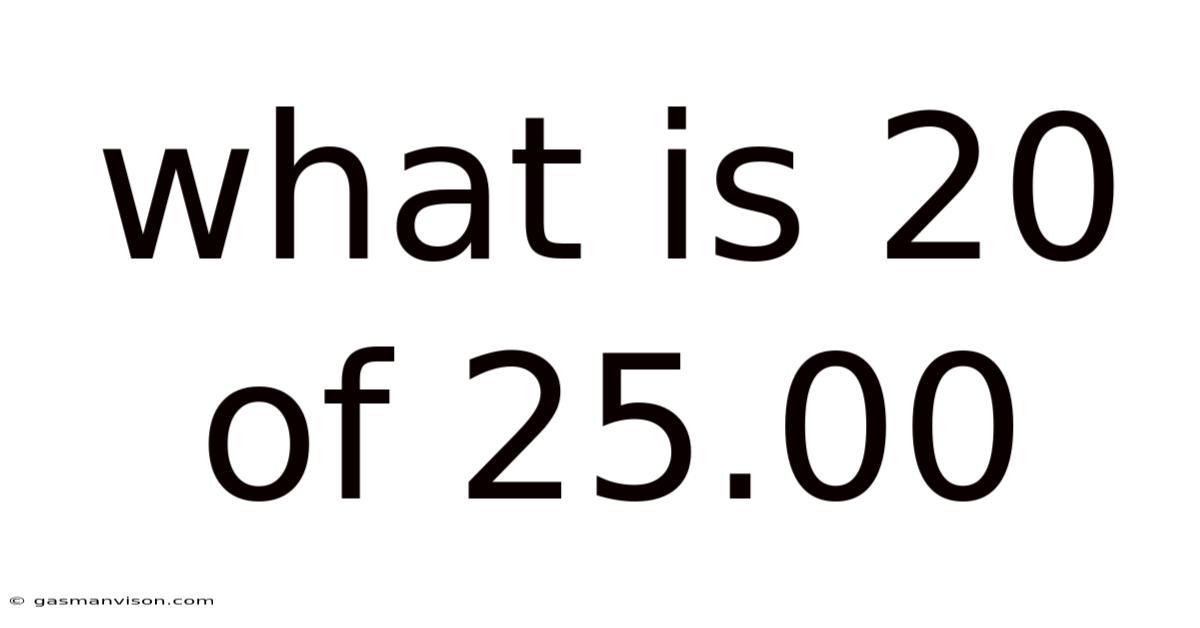
Table of Contents
What is 20 of 25.00? Understanding Percentages, Fractions, and Decimals
This seemingly simple question, "What is 20 of 25.00?", delves into fundamental mathematical concepts crucial for various applications, from everyday budgeting to complex financial calculations. This article will explore this question thoroughly, explaining the different ways to approach the problem and highlighting the underlying principles of percentages, fractions, and decimals. We'll also touch upon practical applications and demonstrate how to solve similar problems.
What the Question Really Asks:
The question "What is 20 of 25.00?" is essentially asking to find the value representing 20 out of 25.00, or what proportion 20 represents of the total 25.00. This is a classic percentage problem, but it can also be solved using fractions and decimals.
Method 1: Using Fractions
The most straightforward method is to express the problem as a fraction:
- The fraction: 20/25.00
This fraction represents 20 parts out of a total of 25 parts. To simplify this fraction, we find the greatest common divisor (GCD) of 20 and 25, which is 5. Dividing both the numerator (20) and the denominator (25) by 5, we get:
- Simplified fraction: 4/5
This means that 20 out of 25 is equivalent to 4 out of 5. This simplified fraction is easier to work with and understand.
To express this fraction as a decimal, divide the numerator by the denominator:
- Decimal equivalent: 4 ÷ 5 = 0.8
Therefore, 20 out of 25.00 is equal to 0.8.
Method 2: Using Percentages
Percentages provide another way to represent the proportion. A percentage represents a fraction out of 100. To find the percentage, we can use the following formula:
(Part / Whole) x 100%
In this case:
(20 / 25) x 100% = 0.8 x 100% = 80%
Therefore, 20 is 80% of 25.00.
Method 3: Using Decimal Multiplication
We can also solve this problem using decimal multiplication. Since we've already established that 20/25 = 0.8, we can think of the problem as finding 0.8 of 25.00. To do this, we simply multiply:
0.8 x 25.00 = 20
This confirms that 20 represents 80% of 25.00.
Understanding the Interplay of Fractions, Decimals, and Percentages
These three methods demonstrate the interconnectedness of fractions, decimals, and percentages. They are simply different ways of representing the same proportion. Understanding how to convert between these forms is essential for solving various mathematical problems.
- Fractions to Decimals: Divide the numerator by the denominator.
- Decimals to Percentages: Multiply by 100 and add the % symbol.
- Percentages to Decimals: Divide by 100.
- Decimals to Fractions: Express the decimal as a fraction with a denominator of a power of 10 (e.g., 0.8 = 8/10, which simplifies to 4/5).
- Fractions to Percentages: Convert the fraction to a decimal and then multiply by 100.
Practical Applications:
The ability to calculate proportions, using fractions, decimals, or percentages, is essential in many real-world scenarios:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all involve working with proportions.
- Retail: Determining sale prices, calculating markups, and understanding profit percentages are critical for retailers.
- Science: Expressing experimental results, calculating concentrations, and analyzing data often require working with proportions.
- Everyday Life: Dividing expenses among friends, calculating tips, and understanding discounts all involve the same underlying mathematical principles.
Solving Similar Problems:
Let's consider some similar problems to further solidify understanding:
- What is 15 of 30? This is equivalent to the fraction 15/30, which simplifies to 1/2, or 0.5, or 50%.
- What is 75% of 120? This is (75/100) x 120 = 0.75 x 120 = 90.
- What is 2/3 of 90? This is (2/3) x 90 = 60.
- If 30 is 60% of a number, what is the number? Let the number be x. Then 0.6x = 30. Solving for x, we get x = 30/0.6 = 50.
Advanced Concepts and Considerations:
While this article focuses on basic percentage calculations, more advanced concepts build upon these foundations:
- Compound Interest: Interest earned on both the principal and accumulated interest. This requires understanding exponential growth.
- Statistical Analysis: Percentages are frequently used to represent proportions in data sets. Understanding statistical significance and error margins is important.
- Financial Modeling: Complex financial models rely heavily on percentage calculations to predict future outcomes.
Conclusion:
The question "What is 20 of 25.00?" provides a springboard for understanding fundamental mathematical concepts applicable across numerous fields. By mastering the interplay between fractions, decimals, and percentages, you equip yourself with essential tools for everyday problem-solving and advanced quantitative analysis. The methods illustrated in this article provide a solid foundation for tackling more complex proportional problems and developing a strong mathematical intuition. Remember to practice regularly to solidify your understanding and build confidence in tackling similar calculations. Through consistent practice and application, you'll become proficient in this essential mathematical skill.
Latest Posts
Latest Posts
-
20 Cups How Many Quarts
Sep 25, 2025
-
What Is 5 Of 90
Sep 25, 2025
-
Wxy Is A Right Triangle
Sep 25, 2025
-
Standing Up To Absolute Power
Sep 25, 2025
-
Globalization Has Caused Intercultural Transients
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 25.00 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.