What Is 20 Of 70.00
gasmanvison
Sep 13, 2025 · 5 min read
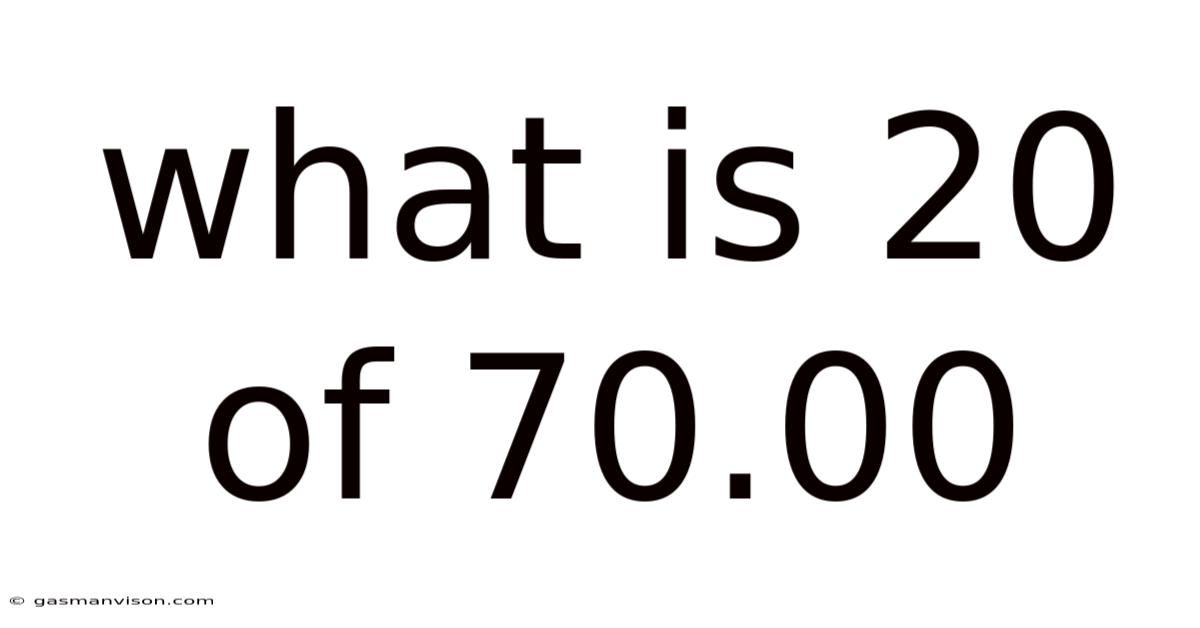
Table of Contents
What is 20% of 70.00? A Comprehensive Guide to Percentage Calculations
This article delves into the seemingly simple question: "What is 20% of 70.00?" While the answer might seem immediately obvious to some, understanding the underlying principles of percentage calculations is crucial for various applications in daily life, finance, and academic pursuits. This guide will not only provide the answer but will also explore different methods of calculating percentages, highlighting their practical uses and offering tips for improving your understanding of this fundamental mathematical concept. We'll cover everything from basic percentage calculation to more complex scenarios, making this a valuable resource for anyone looking to enhance their numerical skills.
Understanding Percentages: A Foundation for Calculation
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "percent" and represents a portion of a whole. Understanding this fundamental concept is key to tackling any percentage-related problem. In essence, percentages allow us to express parts of a whole in a standardized and easily comparable way. For instance, 20% means 20 out of 100, or 20/100, which simplifies to 1/5.
Method 1: The Basic Percentage Formula
The most straightforward way to calculate a percentage of a number is using the basic formula:
(Percentage/100) * Number = Result
Applying this to our question, "What is 20% of 70.00?", we substitute the values:
(20/100) * 70.00 = 14.00
Therefore, 20% of 70.00 is $\boxed{14.00}$
This method is particularly useful for simple percentage calculations and is easily adaptable for mental arithmetic. It's a foundational method that everyone should understand.
Method 2: Converting Percentage to Decimal
Another common approach involves converting the percentage to a decimal before performing the multiplication. To convert a percentage to a decimal, simply divide the percentage by 100. In our case:
20% / 100 = 0.20
Now, multiply the decimal by the number:
0.20 * 70.00 = 14.00
This method is efficient and often preferred when using calculators, as it streamlines the calculation process. The decimal representation is directly usable in many computational applications.
Method 3: Using Proportions
The proportion method offers a slightly different perspective. We can set up a proportion to solve for the unknown value:
20/100 = x/70.00
To solve for 'x', cross-multiply:
100x = 20 * 70.00
100x = 1400
x = 1400 / 100
x = 14.00
This approach is particularly helpful in understanding the relationship between the percentage, the whole, and the part. It provides a visual representation of the problem, making it easier to grasp the underlying concept.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, tips, and profit margins all involve percentage calculations. For example, understanding the interest rate on a loan or the discount on a sale item requires precise percentage calculations. Investment returns are also often expressed as percentages.
-
Retail and Sales: Retailers use percentages extensively for discounts, sales tax calculations, and profit margin analysis. Understanding markups and markdowns requires a solid grasp of percentages.
-
Data Analysis: Percentages are essential for interpreting and presenting data. They allow for easy comparison of proportions within datasets. For example, expressing survey results as percentages makes them more accessible and understandable.
-
Science and Engineering: Percentages are used to express error margins, concentrations, and efficiency in various scientific and engineering applications. For instance, expressing the accuracy of a measurement or the concentration of a solution often involves percentages.
-
Everyday Life: Calculating tips at restaurants, determining the sale price of an item, or understanding tax rates all require basic percentage calculations.
Beyond the Basics: More Complex Percentage Problems
While the example of "What is 20% of 70.00?" is relatively straightforward, percentage problems can become more complex. Here are some examples and how to approach them:
-
Finding the Percentage: If you know the part and the whole, you can calculate the percentage using the formula: (Part/Whole) * 100 = Percentage. For example, if 14 is a part of 70, the percentage is (14/70) * 100 = 20%.
-
Finding the Whole: If you know the part and the percentage, you can find the whole using the formula: (Part / (Percentage/100)) = Whole. For instance, if 14 is 20% of a number, the whole number is (14 / (20/100)) = 70.
-
Percentage Increase/Decrease: These problems involve calculating the percentage change between two values. The formula for percentage increase is: ((New Value - Original Value) / Original Value) * 100. The formula for percentage decrease is similar, but the result will be negative.
-
Compound Percentage: This involves calculating percentages on percentages, such as compound interest. These calculations can be more intricate and may require iterative methods or specialized formulas.
Tips for Mastering Percentage Calculations
-
Practice Regularly: The best way to improve your skills is through consistent practice. Work through various examples and gradually increase the complexity of the problems.
-
Utilize Online Resources: Many websites and apps offer interactive exercises and tutorials on percentage calculations.
-
Use a Calculator Strategically: While mental calculation is beneficial, using a calculator for more complex problems saves time and improves accuracy.
-
Understand the Concepts: Focus on understanding the underlying principles rather than simply memorizing formulas. This approach will help you adapt to different types of percentage problems.
-
Break Down Complex Problems: If you encounter a difficult problem, break it down into smaller, manageable steps. This approach can greatly simplify the calculation process.
Conclusion
The question "What is 20% of 70.00?" serves as a simple yet powerful introduction to the world of percentage calculations. Mastering this fundamental mathematical concept is crucial for navigating various aspects of daily life, from personal finance to professional endeavors. By understanding the different methods, practical applications, and tips provided in this comprehensive guide, you can confidently tackle any percentage problem and enhance your numerical literacy. Remember, practice is key – the more you work with percentages, the more comfortable and proficient you'll become.
Latest Posts
Latest Posts
-
106 Degrees Fahrenheit To Celsius
Sep 13, 2025
-
You Exist In The Context
Sep 13, 2025
-
How Tall Is 2 Meters
Sep 13, 2025
-
75 Kg How Many Lbs
Sep 13, 2025
-
Were Democratic Republicans Anti Federalists
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 70.00 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.