What Is 20 Of 8
gasmanvison
Sep 20, 2025 · 5 min read
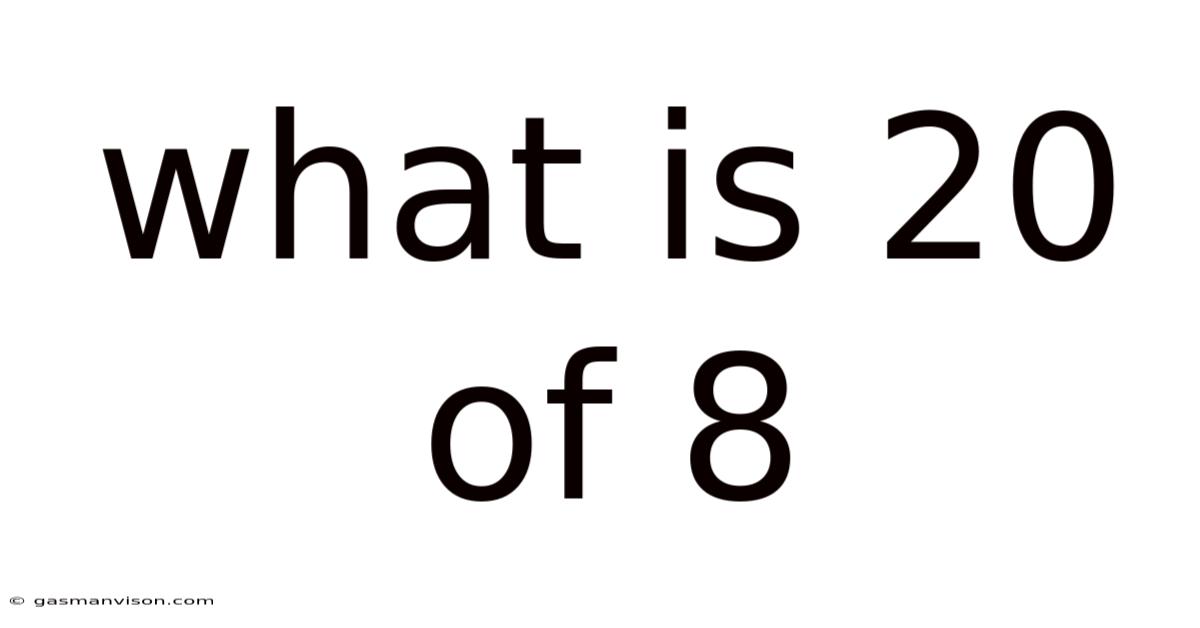
Table of Contents
What is 20% of 8? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 20% of 8?", opens the door to a broader understanding of percentages, their practical applications, and how to calculate them effectively. While the answer itself is straightforward, exploring the underlying concepts provides valuable insights into mathematical problem-solving and real-world applications. This article will not only answer the question but delve into the methods, demonstrate alternative approaches, and explore the relevance of percentages in various fields.
Meta Description: Learn how to calculate 20% of 8 and discover the underlying principles of percentages. This comprehensive guide explores different calculation methods, real-world applications, and expands on the concept of percentage calculations for a deeper understanding.
Understanding Percentages: A Foundation
A percentage is a fraction or ratio expressed as a portion of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Understanding this fundamental definition is crucial for tackling any percentage problem. Think of a percentage as a way to represent a part of a whole, making comparisons and calculations easier. For example, 50% represents 50 out of 100, or one-half. Similarly, 25% is 25 out of 100, or one-quarter.
Calculating 20% of 8: The Direct Approach
The most straightforward method to calculate 20% of 8 involves converting the percentage to a decimal and then multiplying. Here's how:
-
Convert the percentage to a decimal: To convert 20% to a decimal, divide by 100: 20% / 100 = 0.20
-
Multiply the decimal by the number: Multiply the decimal (0.20) by the number (8): 0.20 * 8 = 1.6
Therefore, 20% of 8 is 1.6.
Alternative Methods: Expanding Your Understanding
While the direct approach is efficient, exploring alternative methods deepens our understanding of percentages and offers flexibility in problem-solving.
Method 1: Using Fractions
Percentages can be represented as fractions. 20% can be expressed as 20/100, which simplifies to 1/5. Therefore, calculating 20% of 8 becomes equivalent to finding 1/5 of 8:
8 * (1/5) = 8/5 = 1.6
This method highlights the relationship between fractions and percentages, reinforcing the fundamental concepts.
Method 2: Proportionality
We can also solve this using the concept of proportionality. We can set up a proportion:
20/100 = x/8
Where 'x' represents 20% of 8. To solve for 'x', cross-multiply:
100x = 20 * 8 100x = 160 x = 160 / 100 x = 1.6
This approach emphasizes the proportional relationship between the percentage and the whole number. It’s particularly useful when dealing with more complex percentage problems.
Real-World Applications: Where Percentages Matter
Percentages are ubiquitous in various aspects of daily life and professional fields. Understanding their application is crucial for informed decision-making.
Finance and Budgeting:
- Interest rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts.
- Discounts and sales: Retail stores frequently advertise discounts as percentages (e.g., 20% off).
- Taxes: Taxes are often calculated as a percentage of income or purchase price.
- Investment returns: Investment performance is frequently expressed as a percentage return on investment.
Statistics and Data Analysis:
- Data representation: Percentages are used extensively to represent data visually in charts and graphs.
- Probability and risk assessment: Percentages are used to express probabilities and assess risks in various fields, including insurance and finance.
Science and Engineering:
- Measurements and ratios: Percentages are utilized in scientific experiments and measurements to express ratios and proportions.
- Error analysis: Experimental error is often expressed as a percentage of the measured value.
Everyday Life:
- Tip calculations: Calculating a tip in a restaurant typically involves using percentages.
- Recipe scaling: Adjusting recipe ingredients often involves using percentages to increase or decrease the quantities.
Beyond the Basics: More Complex Percentage Problems
While calculating 20% of 8 is a relatively simple problem, understanding the underlying principles allows you to tackle more complex scenarios. For instance:
-
Finding the original value: If you know a percentage of a number and the resulting value, you can work backward to find the original number. For example, if 20% of a number is 1.6, what is the number? (Answer: 8)
-
Calculating percentage increase or decrease: Determining the percentage change between two values involves calculating the difference and expressing it as a percentage of the original value.
-
Compound interest: Compound interest calculations involve applying percentages repeatedly over time.
Mastering Percentages: Tips and Practice
Consistent practice is key to mastering percentage calculations. Here are some tips to improve your understanding and skills:
- Practice regularly: Solve various percentage problems to build your confidence and familiarity.
- Use different methods: Experiment with different calculation methods to find the approach that best suits your understanding.
- Visualize percentages: Represent percentages visually using diagrams or graphs to aid comprehension.
- Utilize online resources: Several online calculators and tutorials can assist in learning and practicing percentage calculations.
Conclusion: The Power of Percentages
The seemingly simple question, "What is 20% of 8?", serves as a gateway to a vast world of mathematical applications. Understanding percentages is fundamental to navigating various aspects of daily life, from personal finance to professional endeavors. By mastering the core concepts and exploring different calculation methods, you equip yourself with a powerful tool for problem-solving and informed decision-making. Remember that consistent practice and a deeper understanding of the underlying principles are crucial for developing proficiency in percentage calculations and leveraging their power in diverse fields. Through diligent practice and exploration of diverse applications, you can transform your understanding of percentages from a simple calculation to a powerful tool for problem-solving and critical thinking.
Latest Posts
Latest Posts
-
Which Negotiation Tactic Is Refusing
Sep 20, 2025
-
How Much Is 500 Ml
Sep 20, 2025
-
52 Weeks In A Month
Sep 20, 2025
-
Abbreviation For Circle In Address
Sep 20, 2025
-
Molar Mass Iron Iii Oxide
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.