What Is 25 Of 3
gasmanvison
Sep 12, 2025 · 5 min read
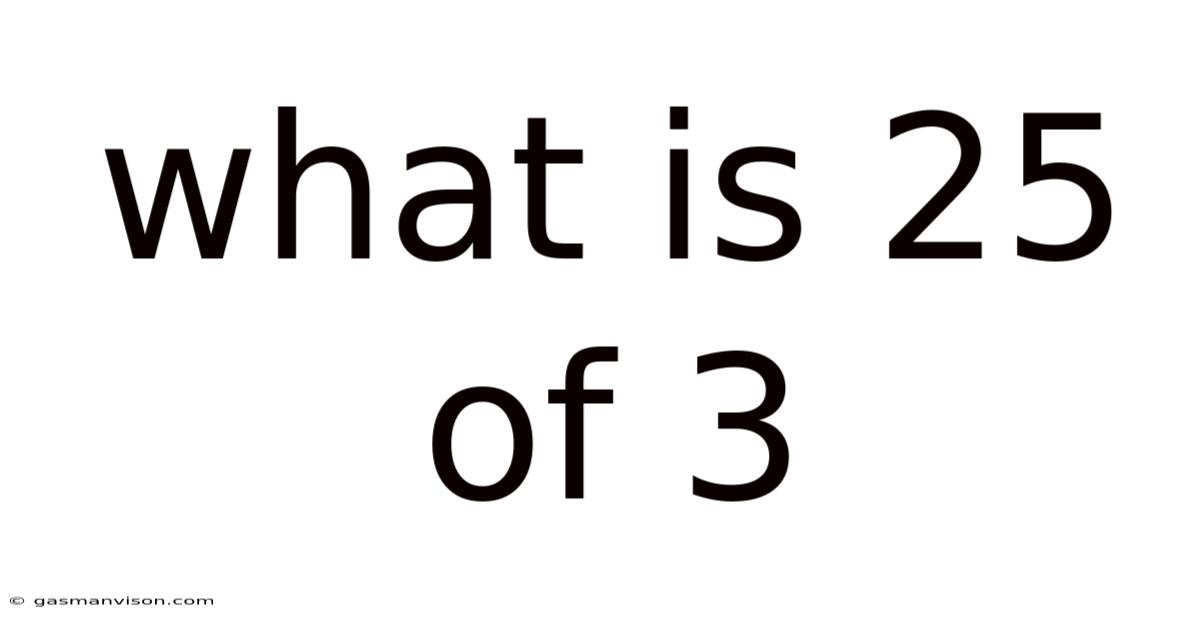
Table of Contents
What is 25% of 3? A Deep Dive into Percentages, Fractions, and Real-World Applications
This seemingly simple question, "What is 25% of 3?", opens the door to a broader understanding of percentages, fractions, decimals, and their practical applications in everyday life. While the answer itself is straightforward, exploring the various methods of calculation and the underlying mathematical concepts provides valuable insights for anyone seeking to improve their numerical literacy. This article will delve into multiple approaches to solve this problem, explaining the logic behind each method and highlighting the interconnectedness of different mathematical concepts.
Understanding the Basics: Percentages, Fractions, and Decimals
Before we tackle the core question, let's refresh our understanding of the fundamental components: percentages, fractions, and decimals. These three represent different ways of expressing parts of a whole.
-
Percentages: A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" denotes "per cent" or "out of one hundred." For example, 25% means 25 out of 100, or 25/100.
-
Fractions: A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of parts, and the numerator indicates the number of parts being considered. For example, 1/4 represents one part out of four equal parts.
-
Decimals: Decimals are another way to represent fractions. They use a base-ten system, where the digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For example, 0.25 is equivalent to 25/100.
Method 1: Converting Percentage to Decimal
The most straightforward approach to finding 25% of 3 is to convert the percentage to a decimal and then multiply.
-
Convert the percentage to a decimal: 25% is equivalent to 25/100, which simplifies to 0.25.
-
Multiply the decimal by the number: 0.25 x 3 = 0.75
Therefore, 25% of 3 is 0.75.
This method is efficient and widely applicable for various percentage calculations. It leverages the direct relationship between percentages and decimals, making it easy to perform the calculation using a calculator or even mental math.
Method 2: Converting Percentage to Fraction
Alternatively, we can convert the percentage to a fraction before performing the calculation.
-
Convert the percentage to a fraction: 25% is equal to 25/100.
-
Simplify the fraction: 25/100 simplifies to 1/4.
-
Multiply the fraction by the number: (1/4) x 3 = 3/4
-
Convert the fraction to a decimal (optional): 3/4 is equal to 0.75.
This method emphasizes the fractional representation of percentages and showcases the equivalence between fractions and decimals. It's particularly useful for understanding the underlying relationships between different mathematical representations. Simplifying the fraction before multiplication can often make the calculation easier.
Method 3: Using Proportions
Proportions offer a more visual and conceptual approach to solving percentage problems. A proportion sets up an equivalence between two ratios.
-
Set up a proportion: We can represent the problem as a proportion: 25/100 = x/3, where 'x' represents the unknown value (25% of 3).
-
Cross-multiply: Cross-multiplying gives us: 100x = 75.
-
Solve for x: Dividing both sides by 100, we get x = 0.75.
This method highlights the proportional relationship between the percentage and the resulting value. It’s a powerful technique that extends beyond simple percentage calculations and can be applied to more complex scenarios involving ratios and proportions.
Real-World Applications of Percentage Calculations
Understanding how to calculate percentages is crucial in many real-world situations. Here are a few examples:
-
Sales and Discounts: Calculating discounts on sale items. For example, a 25% discount on a $12 item would be 0.25 x $12 = $3.
-
Taxes: Determining the amount of sales tax or income tax payable.
-
Tips and Gratuities: Calculating appropriate tips in restaurants or other service industries.
-
Interest Rates: Understanding interest earned on savings accounts or interest paid on loans.
-
Financial Analysis: Analyzing financial statements, including profit margins, return on investment (ROI), and other key performance indicators (KPIs).
-
Statistics and Data Analysis: Interpreting statistical data, such as percentages representing market share or survey results.
-
Scientific Measurements and Experiments: Expressing experimental results and uncertainties as percentages.
Expanding the Concept: Beyond 25% of 3
While this article focused on the specific calculation of 25% of 3, the principles and methods discussed are applicable to a wide range of percentage problems. By mastering these techniques, you can confidently tackle more complex percentage calculations involving larger numbers, different percentages, and various real-world scenarios. For instance, calculating 15% of 200, 7.5% of 500, or even finding what percentage one number represents of another all rely on the same fundamental concepts.
Advanced Concepts and Further Exploration
For those seeking a deeper understanding of percentages and related concepts, further exploration could include:
-
Compound Interest: Understanding how interest accumulates over time when interest is calculated on both the principal and accumulated interest.
-
Percentage Change: Calculating the percentage increase or decrease between two values.
-
Percentage Points: Distinguishing between percentage change and percentage points.
-
Statistical Significance: Understanding how percentages are used in statistical hypothesis testing.
Conclusion:
The seemingly simple question, "What is 25% of 3?", provides a gateway to a wealth of mathematical concepts and practical applications. By understanding the different methods for calculating percentages—converting to decimals, using fractions, or applying proportions—we gain a powerful tool for navigating numerous real-world scenarios. This knowledge extends far beyond simple calculations, enabling us to interpret data, analyze financial information, and make informed decisions in various aspects of life. The ability to confidently handle percentages is a valuable skill that enhances numerical literacy and problem-solving abilities. Therefore, mastering this fundamental mathematical concept lays a solid foundation for tackling more complex mathematical challenges in the future.
Latest Posts
Latest Posts
-
1500 Meter To Mile Conversion
Sep 12, 2025
-
Appropriate Switches For Belt Sanders
Sep 12, 2025
-
Sf6 Molecular Geometry Bond Angle
Sep 12, 2025
-
What Does H 3 2 Represent
Sep 12, 2025
-
6 Ft 4 In Inches
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.