What Is 25 Of 45
gasmanvison
Sep 18, 2025 · 4 min read
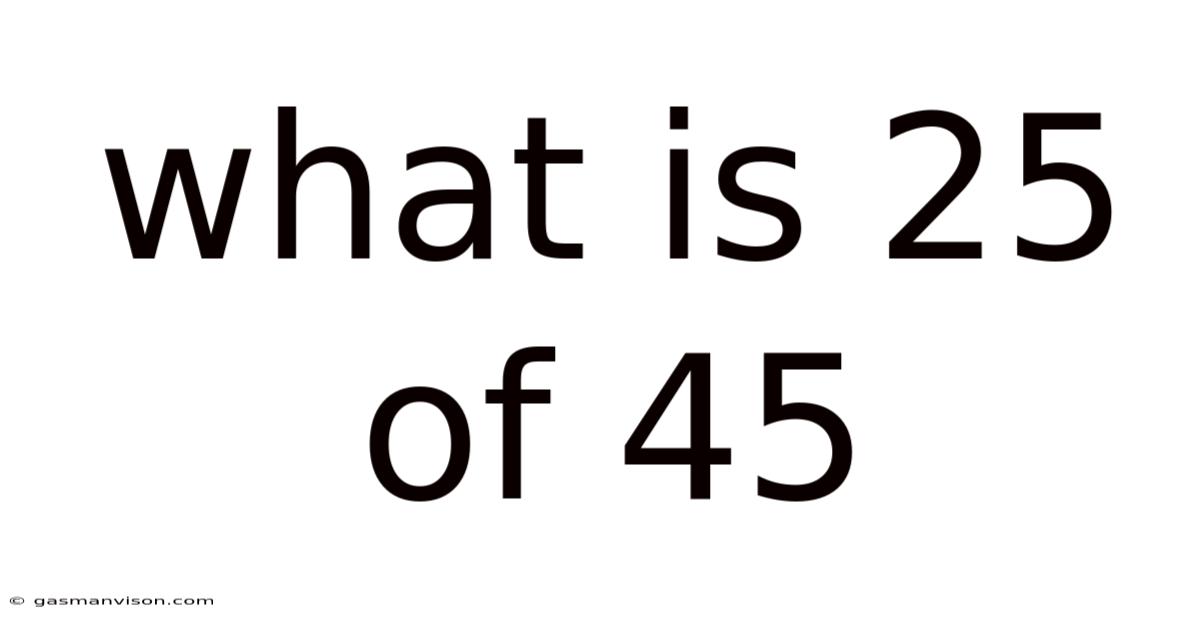
Table of Contents
What is 25 of 45? Unpacking Percentages, Fractions, and Ratios
This seemingly simple question, "What is 25 of 45?", opens the door to a deeper understanding of fundamental mathematical concepts. It's more than just a single answer; it's a gateway to exploring percentages, fractions, ratios, and their practical applications in everyday life. This article will not only provide the answer but also delve into the various methods for calculating it and the broader mathematical principles involved. Understanding these principles empowers you to solve similar problems quickly and efficiently, regardless of the specific numbers involved.
What the Question Means and How to Interpret It
The question "What is 25 of 45?" can be interpreted in several ways, each leading to a slightly different approach:
- Finding a Fraction: This interpretation asks what fraction 25 represents of the whole number 45. This translates to the fraction 25/45.
- Calculating a Percentage: This asks what percentage 25 represents of 45. This requires converting the fraction to a percentage.
- Determining a Ratio: The question can also be understood as finding the ratio of 25 to 45. This is expressed as 25:45.
Regardless of the interpretation, the core mathematical operation remains the same: determining the relationship between 25 and 45.
Method 1: Calculating the Fraction (25/45)
The most straightforward approach is to express the relationship as a fraction: 25/45. This fraction can be simplified by finding the greatest common divisor (GCD) of both the numerator (25) and the denominator (45). The GCD of 25 and 45 is 5. Dividing both the numerator and the denominator by 5 simplifies the fraction:
25 ÷ 5 = 5 45 ÷ 5 = 9
Therefore, 25/45 simplifies to 5/9. This means that 25 represents 5/9 of 45.
Method 2: Converting to a Percentage
To express the relationship as a percentage, we first calculate the fraction (as shown above) and then convert it to a percentage. We already know the simplified fraction is 5/9. To convert a fraction to a percentage, we divide the numerator by the denominator and multiply the result by 100:
(5 ÷ 9) × 100 ≈ 55.56%
Therefore, 25 represents approximately 55.56% of 45.
Method 3: Understanding Ratios
A ratio is a way to compare two quantities. The ratio of 25 to 45 is written as 25:45. Like the fraction, this ratio can be simplified by dividing both numbers by their GCD (which is 5):
25 ÷ 5 = 5 45 ÷ 5 = 9
The simplified ratio is 5:9. This means that for every 5 units of one quantity, there are 9 units of the other quantity. Ratios are often used in scaling, comparing proportions, and various real-world applications, such as in recipes, maps, and architectural drawings.
Practical Applications and Real-World Examples
Understanding percentages, fractions, and ratios is crucial in numerous real-world scenarios:
- Sales and Discounts: Imagine a store offering a 25% discount on an item priced at $45. Using the percentage calculation above, we know the discount amount is approximately $25 (45 x 0.5556).
- Recipe Scaling: If a recipe calls for 25 grams of flour for every 45 grams of sugar, the ratio 5:9 helps you adjust the recipe based on your needs. If you want to use 10 grams of flour, you would need 18 grams of sugar, maintaining the 5:9 ratio.
- Data Analysis: In data analysis and statistics, percentages and ratios are fundamental for interpreting data sets. For example, if 25 out of 45 survey respondents prefer a particular brand, you can express this as a percentage (approximately 55.56%) or a ratio (5:9) to understand consumer preferences.
- Finance and Investments: Understanding percentage changes in stock prices, interest rates, and investment returns is critical for financial planning.
- Construction and Engineering: Ratios are used extensively in construction and engineering to maintain proportions and scale drawings.
Beyond the Basics: More Complex Scenarios
While the problem "What is 25 of 45?" is relatively simple, it lays the foundation for solving more complex problems involving percentages, fractions, and ratios. For instance:
- Finding the Whole: If 25 represents 55.56% of a certain number, you can use the formula: (Part / Percentage) x 100 = Whole to determine the original number. In this case, (25 / 0.5556) x 100 ≈ 45.
- Inverse Proportions: Understanding inverse proportions is essential for scenarios where an increase in one quantity leads to a decrease in another, and vice-versa.
- Compound Percentages: Compound percentages involve applying a percentage to a value multiple times, such as calculating compound interest in finance.
Mastering Mathematical Concepts for Real-World Success
The seemingly simple question, "What is 25 of 45?", serves as a powerful illustration of the interconnectedness of fundamental mathematical concepts. By understanding percentages, fractions, and ratios, and by mastering the methods for converting between them, you equip yourself with valuable skills applicable to a wide range of situations in your personal and professional life. These concepts are not merely abstract mathematical exercises; they are practical tools that enhance your problem-solving abilities and enable you to navigate the complexities of the world around you more effectively. The ability to interpret and manipulate these concepts is increasingly important in today's data-driven world. Continuous practice and a deeper exploration of these concepts will further solidify your understanding and enhance your numerical literacy.
Latest Posts
Latest Posts
-
Are The Triangles Below Similar
Sep 18, 2025
-
Images Cannot Be Considered Sources
Sep 18, 2025
-
Tablespoon Of Sugar To Grams
Sep 18, 2025
-
Find The Measure Of Bd
Sep 18, 2025
-
5 Divided By 5 6
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.