What Is 25 Of 520
gasmanvison
Sep 10, 2025 · 4 min read
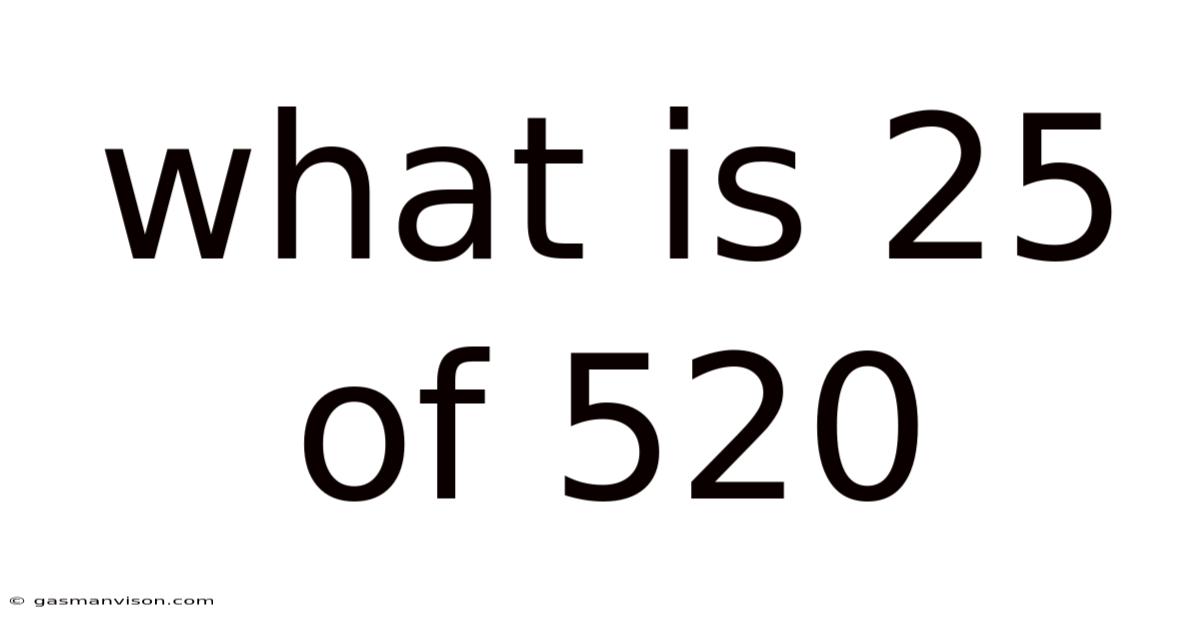
Table of Contents
What is 25/520? Unveiling the Power of Fractions and Percentages
This seemingly simple question, "What is 25/520?", opens the door to a deeper understanding of fractions, percentages, and their applications in everyday life. This article will explore not only the numerical answer but also the broader mathematical concepts involved, showing you how to solve this problem and similar ones with confidence. We'll also delve into practical applications and explore the significance of understanding fractional and percentage calculations.
Meta Description: Learn how to calculate 25/520 and understand the underlying principles of fractions and percentages. This comprehensive guide covers simplification, decimal conversion, and real-world applications, empowering you with essential math skills.
Understanding Fractions: A Foundation of Mathematics
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In our case, 25/520, 25 is the numerator and 520 is the denominator. This fraction means 25 out of 520 parts.
Key Concepts:
- Numerator: The number of parts you have.
- Denominator: The total number of parts in the whole.
Understanding this basic structure is crucial for solving any fractional problem.
Simplifying Fractions: Finding the Greatest Common Divisor (GCD)
Before calculating the decimal equivalent, it's often beneficial to simplify the fraction. Simplifying means reducing the numerator and denominator to their smallest possible whole numbers while maintaining the same value. This is done by finding the greatest common divisor (GCD) of both numbers. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
For 25 and 520, we can find the GCD using several methods. One common approach is to list the factors of each number:
- Factors of 25: 1, 5, 25
- Factors of 520: 1, 2, 4, 5, 10, 13, 20, 26, 40, 52, 65, 104, 130, 260, 520
The greatest common factor is 5. Therefore, we can simplify the fraction:
25/520 = (25 ÷ 5) / (520 ÷ 5) = 5/104
Converting Fractions to Decimals: Division is Key
Now that we have the simplified fraction 5/104, we can convert it into a decimal. To do this, we simply divide the numerator by the denominator:
5 ÷ 104 ≈ 0.0480769
This decimal representation gives us a more readily understandable value compared to the fraction. Rounding to a suitable number of decimal places depends on the context. For instance, we might round to 0.048 or 0.05 depending on the required level of precision.
Converting Fractions to Percentages: Multiplying by 100
Percentages provide another way to express the fraction. A percentage represents a fraction out of 100. To convert a decimal to a percentage, we multiply by 100:
0.0480769 x 100 ≈ 4.81% (rounded to two decimal places)
Therefore, 25/520 is approximately equal to 4.81%. This means that 25 represents approximately 4.81% of 520.
Practical Applications of Fractions and Percentages
Understanding fractions and percentages is crucial in various real-world scenarios:
- Finance: Calculating interest rates, discounts, and profit margins. For example, if you receive a 4.81% discount on a $520 item, you'll save approximately $25.
- Statistics: Representing data as proportions or probabilities. For instance, if 25 out of 520 people surveyed prefer a particular brand, this represents a 4.81% market share.
- Cooking and Baking: Following recipes that require fractional measurements of ingredients.
- Construction and Engineering: Precise measurements and calculations are essential, often involving fractions.
- Data Analysis: Understanding data ratios and proportions is crucial for drawing meaningful insights.
Beyond the Basics: More Advanced Fraction Operations
While this article focuses on the core concepts, mastering fractions involves more advanced operations, such as:
- Adding and Subtracting Fractions: Requires finding a common denominator.
- Multiplying Fractions: Multiply the numerators together and the denominators together.
- Dividing Fractions: Invert the second fraction and multiply.
Mastering Fractions and Percentages: A Continuous Journey
This comprehensive guide helps to illustrate how to calculate 25/520 and illuminates the broader mathematical context. Remember that understanding fractions and percentages isn't just about solving equations; it's about developing a fundamental understanding of representing parts of a whole. From everyday finances to complex scientific calculations, these skills are indispensable. By practicing these techniques and exploring more advanced concepts, you'll improve your numerical literacy and problem-solving abilities significantly. The seemingly simple question, "What is 25/520?", has thus led us on a journey exploring the fascinating world of fractions and percentages, highlighting their importance in various aspects of life. Continue practicing, explore further resources, and you’ll be surprised at how much easier navigating the world of numbers becomes. Continue learning, and you will soon find yourself comfortably handling more complex calculations involving fractions and percentages. The ability to manipulate these numerical representations confidently opens doors to deeper understanding in various fields.
Latest Posts
Latest Posts
-
Respondeat Superior Is Associated With
Sep 10, 2025
-
Molar Mass Of Barium Acetate
Sep 10, 2025
-
What Does Layout Columns Do
Sep 10, 2025
-
What Equals 64 In Multiplication
Sep 10, 2025
-
How To Measure 12 Ounces
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 520 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.