What Is 256 Square Root
gasmanvison
Sep 21, 2025 · 6 min read
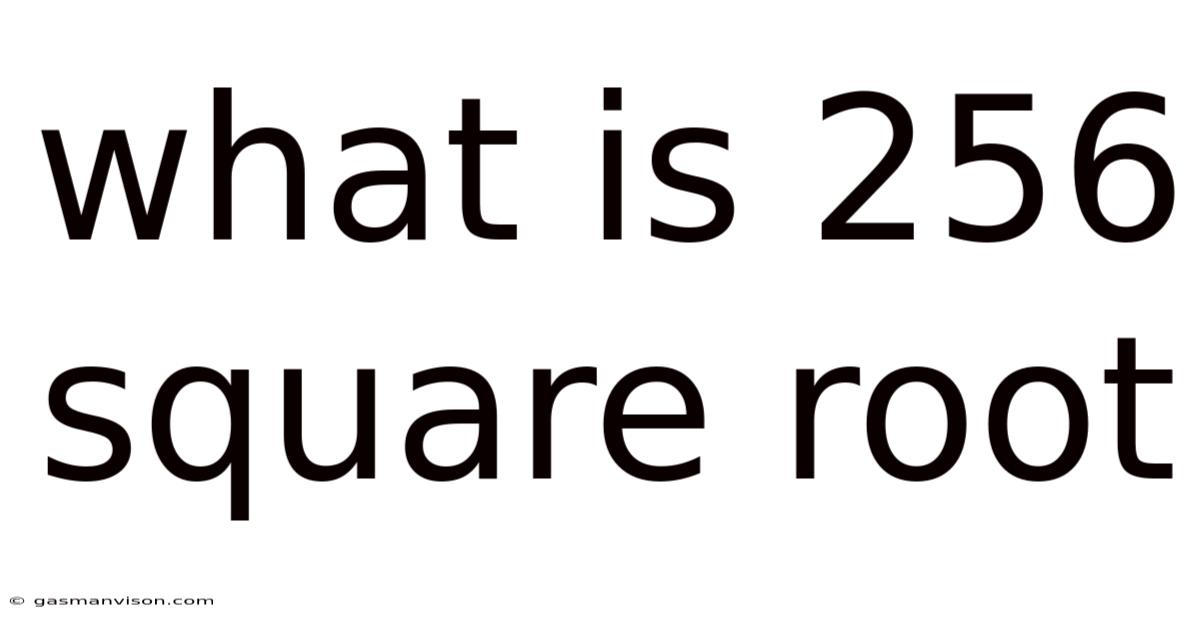
Table of Contents
What is the Square Root of 256? Understanding Square Roots and Their Applications
The square root of 256 is a fundamental concept in mathematics with wide-ranging applications across various fields. This article delves deep into understanding what the square root of 256 is, how to calculate it, and its significance in different contexts. We'll explore various methods for finding the square root, discuss related mathematical concepts, and highlight practical applications of this seemingly simple calculation. By the end, you'll have a comprehensive grasp of the square root of 256 and its relevance beyond basic arithmetic.
What is a Square Root?
Before diving into the specifics of the square root of 256, let's establish a clear understanding of what a square root represents. Simply put, the square root of a number is a value that, when multiplied by itself (squared), gives the original number. For example, the square root of 9 is 3 because 3 x 3 = 9. This is often represented mathematically as √9 = 3. The symbol '√' is the radical symbol, indicating the square root operation.
Calculating the Square Root of 256
There are several ways to calculate the square root of 256:
1. Prime Factorization:
This method involves breaking down the number 256 into its prime factors. Prime factorization is a process of expressing a number as a product of prime numbers (numbers divisible only by 1 and themselves).
- 256 = 2 x 128
- 128 = 2 x 64
- 64 = 2 x 32
- 32 = 2 x 16
- 16 = 2 x 8
- 8 = 2 x 4
- 4 = 2 x 2
Therefore, the prime factorization of 256 is 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2, or 2⁸. To find the square root, we pair the factors and take one factor from each pair. Since we have eight 2s, we have four pairs. Taking one from each pair, we get 2 x 2 x 2 x 2 = 16. Therefore, the square root of 256 is 16.
2. Using a Calculator:
The most straightforward method is using a calculator. Most calculators have a dedicated square root function (√). Simply input 256 and press the square root button to obtain the answer: 16.
3. Estimation and Trial and Error:
For smaller numbers, estimation and trial and error can be effective. We know that 10² = 100 and 20² = 400. Since 256 lies between 100 and 400, the square root must be between 10 and 20. By trying numbers within this range (12, 13, 14, etc.), we can eventually arrive at 16 as the square root.
Understanding Perfect Squares
The number 256 is a perfect square. A perfect square is a number that can be obtained by squaring an integer (a whole number). In other words, it's the result of multiplying an integer by itself. The fact that 256 is a perfect square simplifies its square root calculation. Not all numbers are perfect squares; for example, the square root of 2 is an irrational number (a number that cannot be expressed as a simple fraction).
Applications of Square Roots
The concept of square roots, including the square root of 256, has numerous applications across diverse fields:
1. Geometry:
Square roots are fundamental in geometry for calculating lengths and areas. For instance, the Pythagorean theorem (a² + b² = c²) uses squares and square roots to determine the length of the hypotenuse (c) of a right-angled triangle given the lengths of its other two sides (a and b). If a square has an area of 256 square units, its side length would be √256 = 16 units. This is commonly used in construction, architecture, and surveying.
2. Physics and Engineering:
Square roots appear frequently in physics and engineering calculations involving vectors, velocities, and energies. For example, in calculating the magnitude of a vector, square roots are essential. Moreover, certain physical laws, such as the relationship between distance, velocity, and time, involve square roots. Calculating the speed of an object using kinematic equations can often result in the application of square roots.
3. Data Analysis and Statistics:
Standard deviation, a crucial measure in statistics used to quantify the amount of variation or dispersion in a set of data values, involves calculating the square root of the variance. Variance is the average of the squared differences from the mean. Therefore, the square root is needed to bring the units back to the original units of measurement. This is critical in understanding data distribution and making inferences.
4. Computer Graphics and Game Development:
In computer graphics and game development, square roots are used extensively in calculations involving distances between points, rotations, and transformations. Rendering images and simulations requires numerous geometric calculations, where square roots are integral. For example, determining the distance between two objects in a 3D space would involve the Pythagorean theorem and thus square roots.
5. Financial Mathematics:
Square roots are applied in financial models and calculations involving compound interest and present value computations. These are useful for investors determining returns or future values of investments.
6. Number Theory:
In number theory, square roots play a key role in analyzing the properties of integers, such as determining whether a number is a perfect square or identifying prime numbers. This area of mathematics forms the basis of cryptography.
7. Signal Processing:
Square roots appear in signal processing operations such as root mean square (RMS) calculations which are fundamental to measuring the effective value of alternating current (AC) signals. RMS values are commonly used to represent the average power of a signal.
Beyond the Square Root of 256:
While this article focuses on the square root of 256, the principles and applications discussed extend to finding the square root of any number. Understanding the fundamental concept of square roots and the various methods for calculating them equips you to tackle more complex mathematical problems in diverse fields. Furthermore, the ability to recognize and interpret perfect squares becomes valuable in advanced mathematics and related subjects.
Conclusion:
The square root of 256, which is 16, is a seemingly simple concept but holds significant importance across various fields. Understanding how to calculate it through different methods and appreciating its applications in geometry, physics, statistics, and computer science provides a valuable foundation for further mathematical exploration and problem-solving. The ability to swiftly calculate and utilize square roots enhances your capacity to analyze data, solve complex problems, and understand the underlying mathematical principles governing our world. From basic geometric calculations to advanced signal processing, the humble square root remains a powerful tool in the arsenal of mathematical problem solvers.
Latest Posts
Latest Posts
-
Which Formation Type Ineligible Receiver
Sep 21, 2025
-
What Event Occurs During Translocation
Sep 21, 2025
-
3 4 Fluid Ounces To Ml
Sep 21, 2025
-
Noble Gas Notation For Magnesium
Sep 21, 2025
-
What Is 3 Of 6000
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 256 Square Root . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.