What Is 3/4 In Half
gasmanvison
Sep 13, 2025 · 5 min read
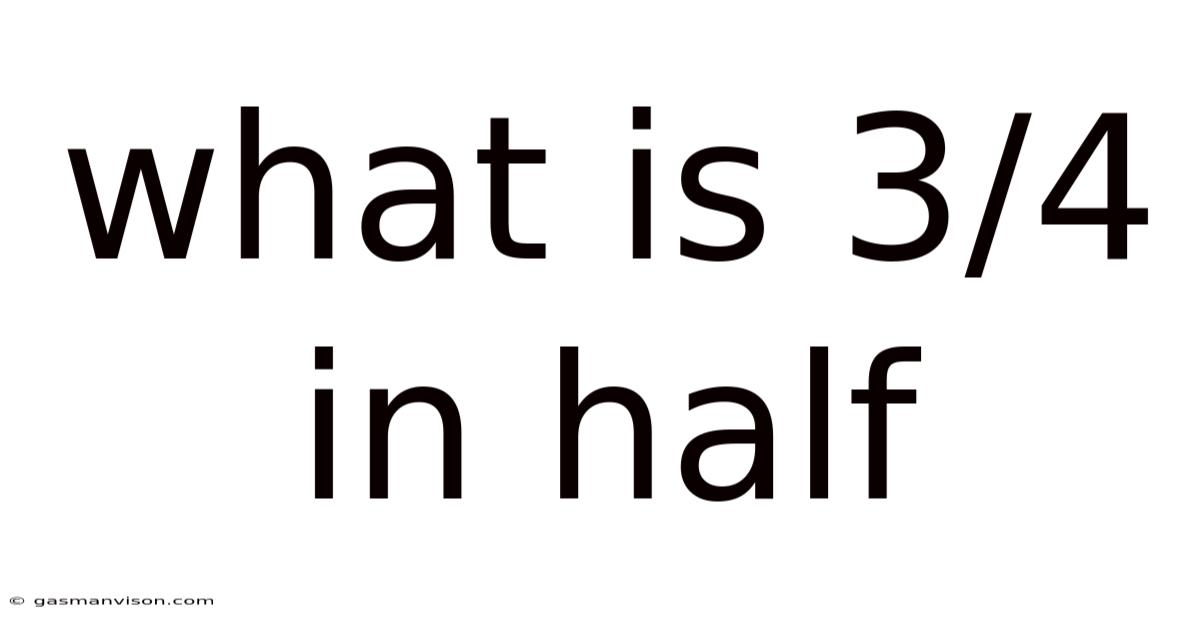
Table of Contents
What is 3/4 in Half? Deconstructing Fractions and Exploring Division
This seemingly simple question, "What is 3/4 in half?", delves into the fundamental concepts of fractions and division. While the immediate answer might seem obvious, a deeper exploration reveals valuable insights into fractional arithmetic, providing a strong foundation for more complex mathematical concepts. This article will not only answer the question directly but also explore the underlying principles, offering practical examples and various approaches to solving similar problems. Understanding how to divide fractions is crucial for various applications, from baking and cooking to engineering and finance.
Meta Description: Discover how to calculate half of 3/4. This comprehensive guide explores the fundamentals of fraction division, providing practical examples and different approaches to solve similar problems. Learn the underlying principles and master this essential mathematical concept.
Understanding Fractions: A Quick Recap
Before diving into the problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In the fraction 3/4, the numerator is 3, and the denominator is 4. This means we have 3 out of 4 equal parts of a whole.
Finding Half of 3/4: The Direct Approach
To find half of 3/4, we simply divide 3/4 by 2. Remember that dividing by 2 is the same as multiplying by 1/2. Therefore, we can rewrite the problem as:
(3/4) ÷ 2 = (3/4) × (1/2)
When multiplying fractions, we multiply the numerators together and the denominators together:
(3 × 1) / (4 × 2) = 3/8
Therefore, half of 3/4 is 3/8.
Visualizing the Solution: A Pictorial Representation
Visualizing the problem can aid understanding. Imagine a pizza cut into 4 equal slices. 3/4 represents having 3 of these slices. To find half of 3/4, we would divide those 3 slices in half. This results in 6 smaller slices, and since the original pizza had 8 equal slices (4 x 2), we now have 3 out of 8 slices, representing 3/8.
Alternative Approaches: Different Perspectives on Division
While the direct method is straightforward, let's explore alternative approaches to reinforce the concept and highlight the flexibility of fractional arithmetic.
Approach 1: Converting to a Decimal
We can convert the fraction 3/4 to its decimal equivalent (0.75) and then divide by 2:
0.75 ÷ 2 = 0.375
Converting 0.375 back to a fraction:
0.375 = 375/1000
Simplifying the fraction by dividing both the numerator and denominator by their greatest common divisor (125):
375/1000 = 3/8
This confirms our previous result.
Approach 2: Dividing the Numerator
While less common, we can also approach this by dividing the numerator by 2 and keeping the denominator the same. However, this approach only works if the numerator is an even number. Since the numerator (3) is odd, this method is not directly applicable in this specific case. It’s important to understand why this doesn't work here to appreciate the broader rules of fraction division.
Extending the Concept: Working with More Complex Fractions
The principles discussed above can be applied to more complex fraction division problems. Let's consider finding one-third of 5/6:
(5/6) ÷ 3 = (5/6) × (1/3) = 5/18
Or, finding three-quarters of 2/5:
(2/5) × (3/4) = 6/20 = 3/10
These examples demonstrate the consistent application of the fundamental rules of fraction multiplication and division. Remember to always simplify the resulting fraction to its lowest terms.
Practical Applications: Real-World Examples
Understanding fraction division isn't just an academic exercise; it has numerous practical applications in daily life:
-
Cooking and Baking: Recipes often require precise measurements. Dividing fractions helps adjust ingredient quantities. For example, if a recipe calls for 3/4 cup of sugar and you want to halve the recipe, you need to calculate half of 3/4 cup.
-
Construction and Engineering: Precise measurements are critical in construction and engineering. Dividing fractions helps ensure accuracy in calculations for dimensions, materials, and quantities.
-
Finance: Many financial calculations involve fractions and percentages. Understanding fraction division is essential for managing budgets, calculating interest, and understanding financial ratios.
-
Data Analysis: In data analysis and statistics, dealing with proportions and ratios frequently involves fraction manipulation and division.
Common Mistakes to Avoid
While fraction division seems straightforward, some common mistakes can lead to incorrect results:
-
Incorrectly multiplying instead of dividing: Remember that dividing by a fraction is equivalent to multiplying by its reciprocal. Don't simply multiply the numerators and denominators without inverting the second fraction when dividing.
-
Forgetting to simplify: Always simplify the resulting fraction to its lowest terms. This ensures a clear and concise answer.
-
Incorrectly applying the 'divide the numerator' method: This method only works if the numerator is divisible by the divisor and is not a general approach to fraction division.
Conclusion: Mastering Fraction Division
Understanding how to find half of 3/4, or indeed any fraction divided by another, is a foundational skill in mathematics. This article has explored various approaches, emphasizing the importance of understanding the underlying principles. By mastering fraction division, you equip yourself with a valuable tool for tackling more complex mathematical problems and solving practical challenges in various aspects of life. Remember to practice consistently, and you'll find yourself confidently navigating the world of fractions. Through consistent application and a deeper understanding of the principles involved, even complex fractional arithmetic becomes manageable and, dare we say, enjoyable.
Latest Posts
Latest Posts
-
What Is 8 Of 1000
Sep 13, 2025
-
Miles Across The United States
Sep 13, 2025
-
16 Fluid Ounces To Pounds
Sep 13, 2025
-
Article Vii Of The Constitution
Sep 13, 2025
-
39 Degrees Celsius To Fahrenheit
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/4 In Half . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.