What Is 30 Of 250
gasmanvison
Sep 09, 2025 · 5 min read
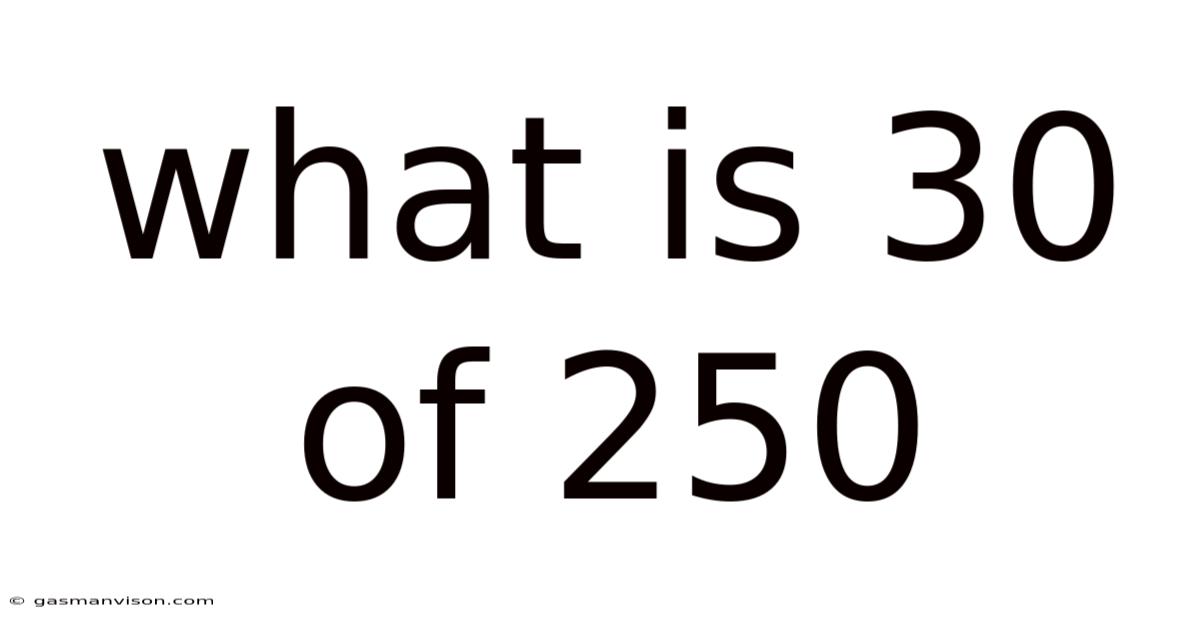
Table of Contents
What is 30 of 250? Unpacking Percentages, Fractions, and Their Real-World Applications
This seemingly simple question, "What is 30 of 250?", opens a door to a world of mathematical concepts with far-reaching applications. It's not just about finding a numerical answer; it's about understanding percentages, fractions, ratios, and how these tools help us interpret data and solve problems in everyday life, from calculating discounts to understanding statistical reports. This comprehensive guide will explore various methods for solving this problem and delve into the broader context of these essential mathematical concepts.
Meta Description: Learn how to calculate 30 of 250, exploring percentages, fractions, ratios, and real-world applications. This in-depth guide covers multiple solution methods and explains the underlying mathematical principles.
Understanding the Problem: 30 out of 250
The phrase "30 of 250" implies a part-to-whole relationship. We're looking to determine what proportion 30 represents when compared to the total of 250. This can be expressed in several ways: as a fraction, a decimal, or a percentage. Each representation offers a different perspective on the same fundamental relationship.
Method 1: Calculating the Percentage
The most common way to express this relationship is as a percentage. A percentage represents a fraction of 100. To calculate the percentage, we use the following formula:
(Part / Whole) * 100%
In our case:
(30 / 250) * 100% = 12%
Therefore, 30 is 12% of 250. This means that 30 represents 12 out of every 100 parts of 250.
Method 2: Expressing it as a Fraction
We can also represent the relationship as a fraction:
30/250
This fraction can be simplified by finding the greatest common divisor (GCD) of 30 and 250. The GCD of 30 and 250 is 10. Dividing both the numerator and the denominator by 10, we get:
3/25
This simplified fraction represents the same proportion as 30/250 but in a more concise form. Both fractions represent the same part-to-whole relationship.
Method 3: Converting the Fraction to a Decimal
To further clarify the relationship, we can convert the simplified fraction 3/25 to a decimal:
3 ÷ 25 = 0.12
This decimal representation, 0.12, is equivalent to 12%, further reinforcing the percentage calculation from Method 1.
Real-World Applications: Why This Matters
Understanding how to calculate percentages and fractions is crucial in numerous everyday scenarios:
-
Discounts and Sales: Imagine a store offering a 12% discount on a $250 item. Knowing that 12% of 250 is 30 allows you to quickly calculate the discount amount ($30) and the final price ($220).
-
Statistical Analysis: In data analysis, understanding proportions is vital. If 30 out of 250 survey respondents answered "yes" to a question, the 12% representation helps in drawing conclusions and visualizing the results. This is fundamental to understanding market research, election polling, and scientific studies.
-
Financial Calculations: From calculating interest rates on loans and investments to determining profit margins in business, percentage calculations are indispensable tools.
-
Recipe Scaling: If a recipe calls for 30 grams of sugar for 250 grams of flour, understanding the proportion (12%) allows you to scale the recipe up or down easily.
-
Probability and Statistics: Probability often involves calculating the likelihood of an event occurring, which frequently involves ratios and percentages. For instance, the probability of selecting a specific item from a group can be represented as a fraction or a percentage.
Expanding the Concepts: Ratios and Proportions
The problem "What is 30 of 250?" also highlights the concept of ratios and proportions. A ratio compares two quantities, while a proportion states that two ratios are equal.
The ratio of 30 to 250 can be written as 30:250 or 3:25 (after simplification). This ratio expresses the relationship between the part (30) and the whole (250). We can use this ratio to solve other problems involving similar proportions. For example, if we have 75 items, we could use the ratio to find out how many represent the same proportion as 30 out of 250:
3/25 = x/75
Solving for x:
x = (3 * 75) / 25 = 9
This demonstrates how understanding proportions enables us to scale up or down the relationship between quantities.
Beyond the Basics: Advanced Applications
The core concepts discussed here – percentages, fractions, ratios, and proportions – lay the foundation for more complex mathematical applications. These include:
-
Compound Interest: This involves calculating interest not just on the principal amount, but also on the accumulated interest. Understanding percentages and their iterative application is vital here.
-
Statistical Inference: Drawing conclusions about a population based on a sample requires a solid understanding of proportions and percentages. This is crucial in fields like medicine, economics, and social sciences.
-
Geometric Progressions: Sequences where each term is found by multiplying the previous term by a constant ratio are used in many areas, such as finance and population growth models. Again, understanding ratios is fundamental.
Conclusion: The Power of Proportions
The seemingly simple question "What is 30 of 250?" provides a springboard for exploring fundamental mathematical concepts with far-reaching practical implications. Mastering the calculation of percentages, fractions, and ratios not only equips you with valuable problem-solving skills but also enhances your ability to interpret and analyze data in various contexts. From everyday transactions to complex scientific studies, these concepts are essential tools for understanding and interacting with the world around us. Understanding the various methods to solve this problem allows for flexibility and a deeper understanding of the underlying mathematical principles. The ability to translate between percentages, fractions, and decimals empowers you to confidently tackle a wide range of quantitative challenges.
Latest Posts
Latest Posts
-
232 90 Th Nuclear Equation
Sep 10, 2025
-
People Who Get More Tickets
Sep 10, 2025
-
How Tall Is 80 Inches
Sep 10, 2025
-
How Much Is 10 Tablespoons
Sep 10, 2025
-
How Are Glamour Waves Created
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.