What Is 30 Of 45
gasmanvison
Sep 12, 2025 · 5 min read
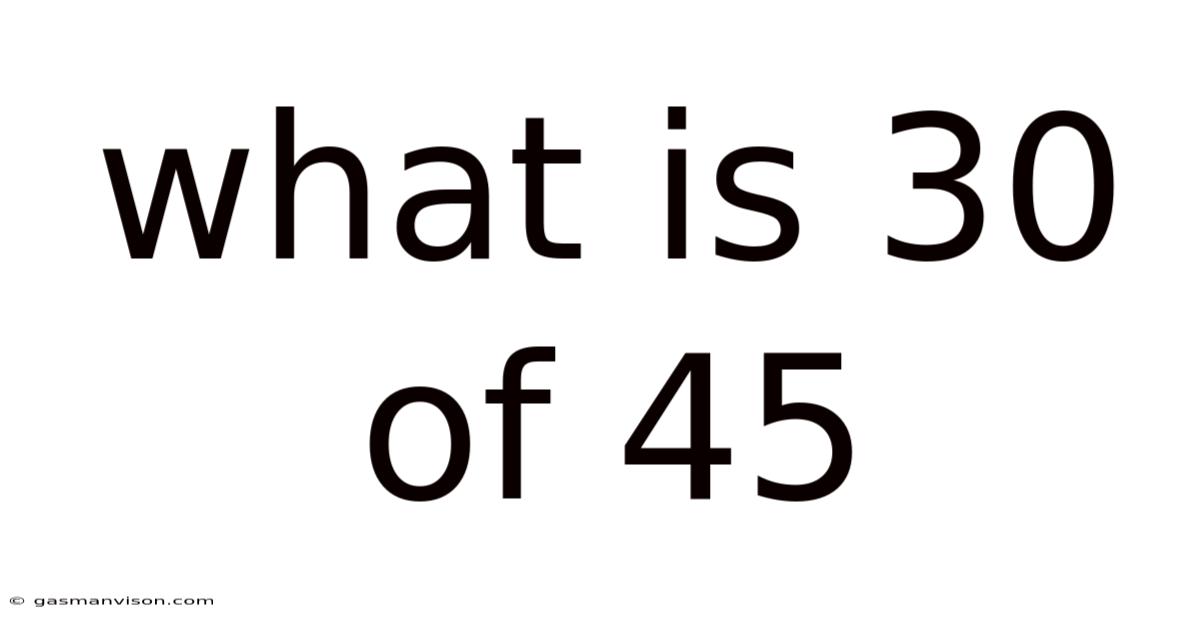
Table of Contents
What is 30 of 45? Decoding Fractions, Percentages, and Ratios
What is 30 of 45? This seemingly simple question opens the door to a deeper understanding of fundamental mathematical concepts like fractions, percentages, and ratios. It's more than just a simple calculation; it's a gateway to grasping proportional relationships and their applications in various fields. This article will explore multiple ways to solve this problem and, more importantly, understand the underlying mathematical principles involved. We'll delve into the practical applications of these concepts, ensuring you're not just getting the answer but also mastering the method.
Understanding the Problem: Fractions, Percentages, and Ratios
At its core, "30 of 45" represents a fractional part of a whole. We can express this relationship in several ways:
- Fraction: 30/45 (thirty forty-fifths)
- Ratio: 30:45 (thirty to forty-five)
- Percentage: The percentage that 30 represents of 45.
Each of these representations provides a unique perspective on the relationship between 30 and 45, and understanding them is crucial for solving similar problems effectively.
Method 1: Simplifying the Fraction
The simplest approach is to express "30 of 45" as a fraction and then simplify it to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator (30) and the denominator (45).
The GCD of 30 and 45 is 15. Dividing both the numerator and the denominator by 15 gives us:
30 ÷ 15 = 2 45 ÷ 15 = 3
Therefore, 30/45 simplifies to 2/3. This means that 30 represents two-thirds of 45.
Method 2: Calculating the Percentage
To express 30 as a percentage of 45, we use the following formula:
(Part / Whole) * 100%
In this case:
(30 / 45) * 100% = 0.666... * 100% ≈ 66.67%
This tells us that 30 is approximately 66.67% of 45. The recurring decimal indicates that the percentage is not a whole number but a repeating decimal. Rounding to two decimal places provides a practical and commonly used representation.
Method 3: Using Ratio and Proportion
Ratios express the relationship between two quantities. The ratio 30:45 can be simplified in the same way as a fraction:
30:45 simplifies to 2:3.
This ratio indicates that for every two parts of one quantity, there are three parts of another. This concept is fundamental in various applications, from scaling recipes to understanding map scales.
Real-World Applications: Where these concepts matter
Understanding fractions, percentages, and ratios is crucial in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, profit margins, and investment returns all involve working with percentages and ratios. For example, understanding how much of a total investment portfolio a certain stock represents.
-
Retail: Determining sale prices, calculating discounts, and understanding profit margins are directly related to percentage calculations. Determining the percentage of a store's revenue from a particular product line is a critical business metric.
-
Cooking and Baking: Scaling recipes up or down requires a thorough understanding of ratios. Increasing or decreasing the quantity of ingredients proportionally maintains the desired taste and consistency.
-
Science and Engineering: Ratios and proportions are fundamental to scientific measurements and engineering calculations, ensuring accurate and consistent results. Calculating concentrations of solutions or analyzing experimental data often involves these concepts.
-
Data Analysis: Expressing data as percentages and ratios simplifies the interpretation and comparison of different datasets. This is especially relevant in fields like market research, public health, and demographics. Understanding the proportion of a population possessing a specific characteristic is essential for analysis and forecasting.
-
Construction and Architecture: Scaling blueprints, calculating material quantities, and determining proportions in architectural design rely heavily on ratios and proportions. Ensuring that elements are proportional to each other and to the whole design is crucial.
-
Everyday Life: From splitting bills equally amongst friends to calculating tip percentages in restaurants, these mathematical concepts permeate our daily routines. Understanding these concepts empowers us to make informed decisions and perform everyday tasks more efficiently.
Expanding the Understanding: Further Exploration
The simple problem "What is 30 of 45?" leads to a deeper exploration of related concepts:
-
Equivalent Fractions: Understanding that 2/3, 4/6, 6/9, and countless other fractions are all equivalent to 30/45 helps in simplifying complex fractions and making comparisons.
-
Decimal Representation: The fraction 2/3 can also be expressed as a recurring decimal (0.666...). Understanding how fractions and decimals are related is essential for working with both forms of numbers.
-
Proportional Reasoning: This is the ability to understand and solve problems involving proportional relationships. This skill is crucial in various fields, including scaling, comparing, and interpreting data.
-
Advanced Ratio Problems: More complex ratio problems involve finding unknown quantities using proportional relationships. These problems require a deeper understanding of ratios and their applications.
Conclusion: More Than Just an Answer
Solving the seemingly simple question "What is 30 of 45?" isn't just about arriving at the answer (2/3 or 66.67%). It's about understanding the underlying principles of fractions, percentages, and ratios and their broad applicability in various contexts. Mastering these concepts equips you with valuable problem-solving skills that extend far beyond the realm of mathematics and into the practical aspects of daily life and various professional fields. By grasping the fundamental relationships between quantities, you'll be better equipped to analyze data, solve problems, and make informed decisions in diverse situations. This understanding forms a strong foundation for more complex mathematical concepts and problem-solving skills. Remember that mathematical proficiency isn't just about calculations; it's about understanding the meaning and relationships behind the numbers.
Latest Posts
Latest Posts
-
Convert 36 3 Celsius To Fahrenheit
Sep 12, 2025
-
60 Is 1 10 Of
Sep 12, 2025
-
If Joe Ran 390 Feet
Sep 12, 2025
-
Molecular Mass Of Aluminum Sulfate
Sep 12, 2025
-
Collaborate Teammate Synonym Or Antonym
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.