What Is 40 Of 160
gasmanvison
Sep 11, 2025 · 4 min read
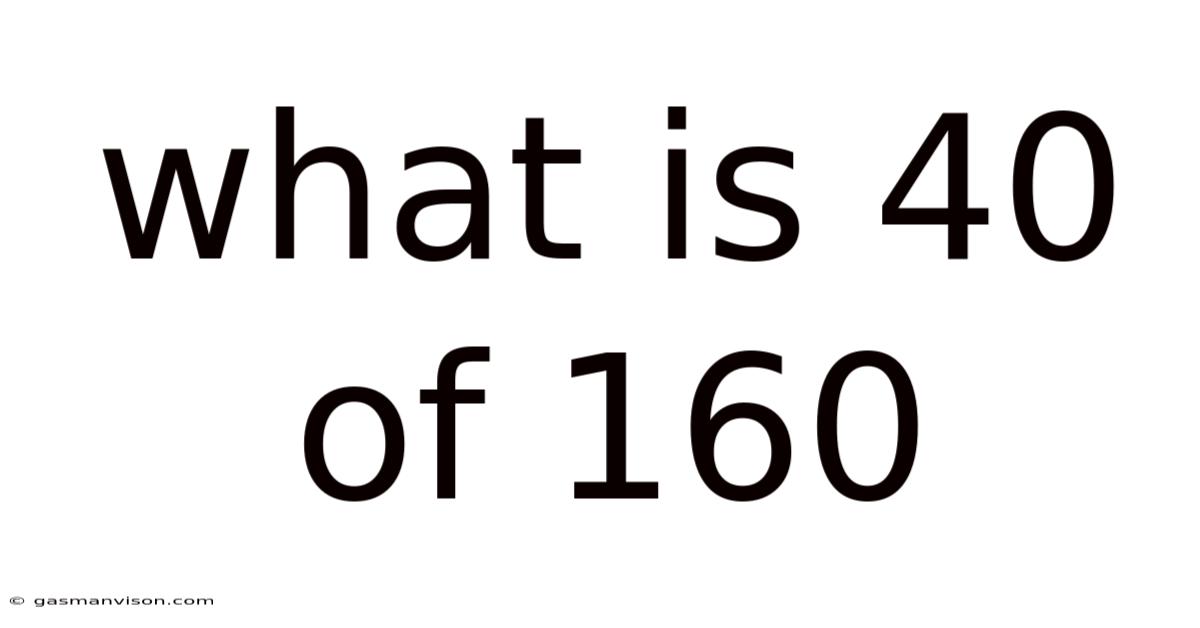
Table of Contents
What is 40 of 160? A Deep Dive into Percentages, Fractions, and Ratios
This seemingly simple question, "What is 40 of 160?", opens the door to a fascinating exploration of fundamental mathematical concepts. It's more than just a straightforward calculation; it's a gateway to understanding percentages, fractions, ratios, and their applications in everyday life. This article will not only provide the answer but also delve into the underlying principles, offering practical examples and demonstrating how to solve similar problems efficiently.
What is 40 out of 160 as a Percentage?
The most common way to interpret "40 of 160" is as a percentage. A percentage represents a fraction of 100. To calculate the percentage, we use the following formula:
(Part / Whole) * 100%
In this case, the part is 40, and the whole is 160. Therefore, the calculation is:
(40 / 160) * 100% = 25%
Therefore, 40 is 25% of 160. This means that 40 represents one-quarter (25%) of the total value of 160. This simple calculation has wide-ranging applications, from calculating discounts in a store to determining the percentage of a population holding a specific characteristic.
Understanding Fractions and Ratios
Beyond percentages, the question also allows us to explore fractions and ratios. A fraction represents a part of a whole, expressed as a numerator (top number) over a denominator (bottom number). In this case, the fraction representing 40 out of 160 is:
40/160
This fraction can be simplified by finding the greatest common divisor (GCD) of 40 and 160, which is 40. Dividing both the numerator and the denominator by 40 simplifies the fraction to:
1/4
This means that 40 out of 160 is equivalent to one-quarter.
A ratio, on the other hand, compares two or more quantities. The ratio of 40 to 160 can be written as:
40:160
Similar to fractions, this ratio can be simplified by dividing both numbers by their GCD (40), resulting in the simplified ratio:
1:4
This simplified ratio indicates that for every one unit of the first quantity, there are four units of the second quantity. Understanding ratios is crucial in various fields, such as scaling recipes, mixing ingredients, or analyzing proportions in scientific experiments.
Real-World Applications and Examples
The concepts of percentages, fractions, and ratios are fundamental to numerous real-world applications. Let's explore a few examples:
-
Sales and Discounts: Imagine a store offering a discount of 40 dollars off an item originally priced at 160 dollars. The discount represents 25% of the original price.
-
Surveys and Statistics: In a survey of 160 people, 40 responded positively to a particular question. This represents 25% of the respondents.
-
Financial Calculations: If you invest 40 dollars out of a total investment of 160 dollars in a specific stock, that represents 25% of your investment portfolio.
-
Recipe Scaling: If a recipe calls for 40 grams of flour for a certain quantity, and you want to scale it up to 160 grams, you're increasing the recipe by a factor of four.
Solving Similar Problems
To efficiently solve similar problems, remember the key formula for percentages:
(Part / Whole) * 100% = Percentage
You can rearrange this formula to find the part or the whole if you know the percentage and one of the other values. For instance:
- Finding the Part: If you know the percentage and the whole, you can find the part using:
(Percentage / 100%) * Whole = Part
- Finding the Whole: If you know the percentage and the part, you can find the whole using:
(Part / Percentage) * 100% = Whole
Advanced Concepts and Further Exploration
The seemingly simple question of "What is 40 of 160?" opens doors to more advanced mathematical concepts. These include:
-
Proportions: Understanding proportions allows us to solve problems where ratios are equivalent. For instance, if the ratio of apples to oranges is 1:4, and we have 10 apples, we can use proportions to find the number of oranges.
-
Algebra: Algebraic equations can be used to solve more complex problems involving percentages, fractions, and ratios.
-
Data Analysis: Understanding percentages, fractions, and ratios is essential for interpreting data, creating charts and graphs, and drawing meaningful conclusions.
Conclusion: More Than Just a Calculation
The question "What is 40 of 160?" transcends a simple calculation. It provides a foundation for understanding core mathematical concepts – percentages, fractions, and ratios – and their real-world applications. Mastering these concepts is crucial for everyday life, from making financial decisions to analyzing data and solving problems in various fields. The ability to calculate percentages, simplify fractions, and understand ratios is a vital skill that enhances problem-solving capabilities and contributes to a more profound understanding of the quantitative world around us. This simple problem, therefore, serves as a powerful gateway to a deeper appreciation of mathematics and its practical significance.
Latest Posts
Latest Posts
-
Most Back Disorders Caused By
Sep 11, 2025
-
What Is 97 8 In Celsius
Sep 11, 2025
-
58 Degrees Fahrenheit To Celsius
Sep 11, 2025
-
How Was Persian Coinage Sophisticated
Sep 11, 2025
-
Summarizing Can Be Used To
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Of 160 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.