What Is 40 Of 25
gasmanvison
Sep 21, 2025 · 5 min read
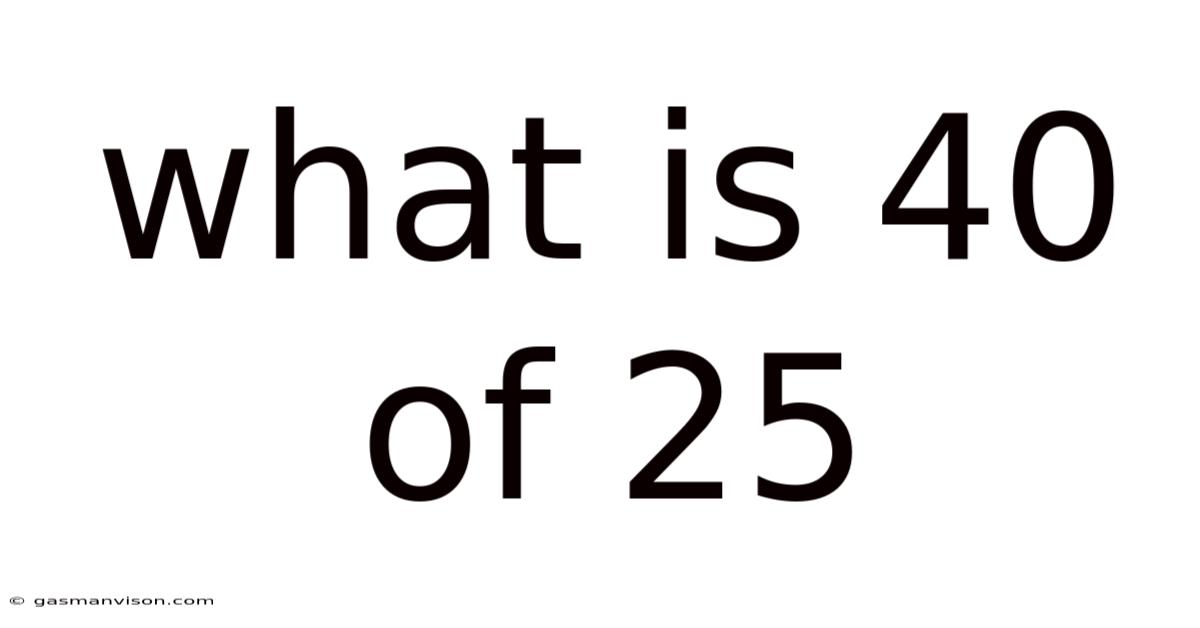
Table of Contents
What is 40% of 25? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 40% of 25?", opens the door to a broader understanding of percentages, their calculation, and their widespread applications in various fields. This article will not only answer the question directly but also explore the underlying mathematical concepts, different calculation methods, and real-world examples demonstrating the importance of percentage calculations. Understanding percentages is crucial for everything from budgeting and finance to data analysis and scientific research.
Meta Description: Learn how to calculate 40% of 25 and explore the broader world of percentages. This comprehensive guide covers different calculation methods, real-world applications, and the importance of percentage understanding in various fields.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred." Therefore, 40% can be written as 40/100 or 0.40 as a decimal. This representation is key to understanding percentage calculations. The core concept involves finding a proportional part of a whole. In our case, we want to find 40% of the whole number 25.
Method 1: Converting to a Decimal
This is perhaps the most straightforward method. We convert the percentage to its decimal equivalent and then multiply it by the number.
- Convert the percentage to a decimal: 40% = 40/100 = 0.40
- Multiply the decimal by the number: 0.40 * 25 = 10
Therefore, 40% of 25 is 10.
Method 2: Using Fractions
This method involves converting the percentage to a fraction and then performing the multiplication.
- Convert the percentage to a fraction: 40% = 40/100
- Simplify the fraction (if possible): 40/100 simplifies to 2/5
- Multiply the fraction by the number: (2/5) * 25 = (2 * 25) / 5 = 50 / 5 = 10
Again, we arrive at the answer: 40% of 25 is 10.
Method 3: Proportion Method
This method uses the concept of proportions to solve the problem. We set up a proportion where x represents the unknown value (40% of 25).
- Set up the proportion: 40/100 = x/25
- Cross-multiply: 40 * 25 = 100 * x
- Solve for x: 1000 = 100x => x = 1000 / 100 = 10
Once more, the answer is 10.
Real-World Applications of Percentage Calculations
Percentage calculations are incredibly versatile and appear in numerous aspects of daily life and professional settings. Here are some examples:
- Finance: Calculating interest on loans, savings accounts, or investments. Understanding discounts and sales tax. Analyzing financial statements and determining profit margins. Calculating percentage changes in stock prices or investment portfolios.
- Retail: Determining discounts offered during sales. Calculating the final price after applying a discount and sales tax. Analyzing sales data to understand the performance of different products or promotions. Calculating markups on products to determine selling prices.
- Science: Expressing experimental results as percentages. Representing data in graphs and charts using percentages. Calculating error margins and statistical significance. Analyzing data sets to identify trends and patterns.
- Healthcare: Determining the percentage of patients with a particular condition. Tracking the effectiveness of treatments through percentage improvement rates. Analyzing epidemiological data to understand disease prevalence and spread. Calculating the success rate of surgical procedures.
- Education: Calculating grades based on percentages of correct answers. Determining the percentage of students who passed or failed a test. Analyzing student performance data to identify areas for improvement. Tracking student progress throughout the academic year.
Beyond the Basics: More Complex Percentage Problems
While the example of finding 40% of 25 is relatively straightforward, percentage problems can become more complex. Here are some examples of more advanced scenarios:
- Finding the original amount: If a discounted item costs $75 after a 25% discount, what was the original price? This requires working backward from the discounted price.
- Calculating percentage increase or decrease: Determining the percentage change between two values, for instance, the increase in sales from one year to the next.
- Compound interest calculations: This involves calculating interest on both the principal amount and accumulated interest from previous periods. This requires understanding exponential growth concepts.
- Percentage points vs. percentages: Distinguishing between a percentage point change and a percentage change. For example, an increase from 10% to 15% is a 5 percentage point increase, but a 50% percentage increase.
Tips for Mastering Percentage Calculations
- Practice regularly: The more you practice, the more comfortable you will become with percentage calculations.
- Understand the concepts: Focus on understanding the underlying principles rather than just memorizing formulas.
- Use different methods: Try different calculation methods to find the approach that works best for you.
- Check your work: Always double-check your answers to ensure accuracy.
- Utilize online resources: There are many online calculators and tutorials available to help you practice and learn more about percentages.
Conclusion: The Ubiquity of Percentages
In conclusion, understanding how to calculate 40% of 25, and indeed any percentage calculation, is a fundamental skill with broad applications across various disciplines. While the basic calculation is relatively simple, mastering the underlying concepts and applying them to more complex scenarios is crucial for success in many fields. This comprehensive guide has covered various methods for solving percentage problems and highlighted their significance in our daily lives and professional endeavors. By grasping the fundamentals and practicing regularly, you can confidently tackle any percentage-related challenge. The seemingly simple question, “What is 40% of 25?” has thus led us on a journey into the fascinating and essential world of percentages. Remember to practice and apply this knowledge to enhance your problem-solving skills and improve your understanding of quantitative information.
Latest Posts
Latest Posts
-
Which Two Expressions Are Equivalent
Sep 21, 2025
-
What Is 10 X 10
Sep 21, 2025
-
Things That Rhyme With End
Sep 21, 2025
-
5 Divided By 3 7
Sep 21, 2025
-
How Many Pounds Is 82kg
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.