What Is 5 Of 120
gasmanvison
Sep 24, 2025 · 5 min read
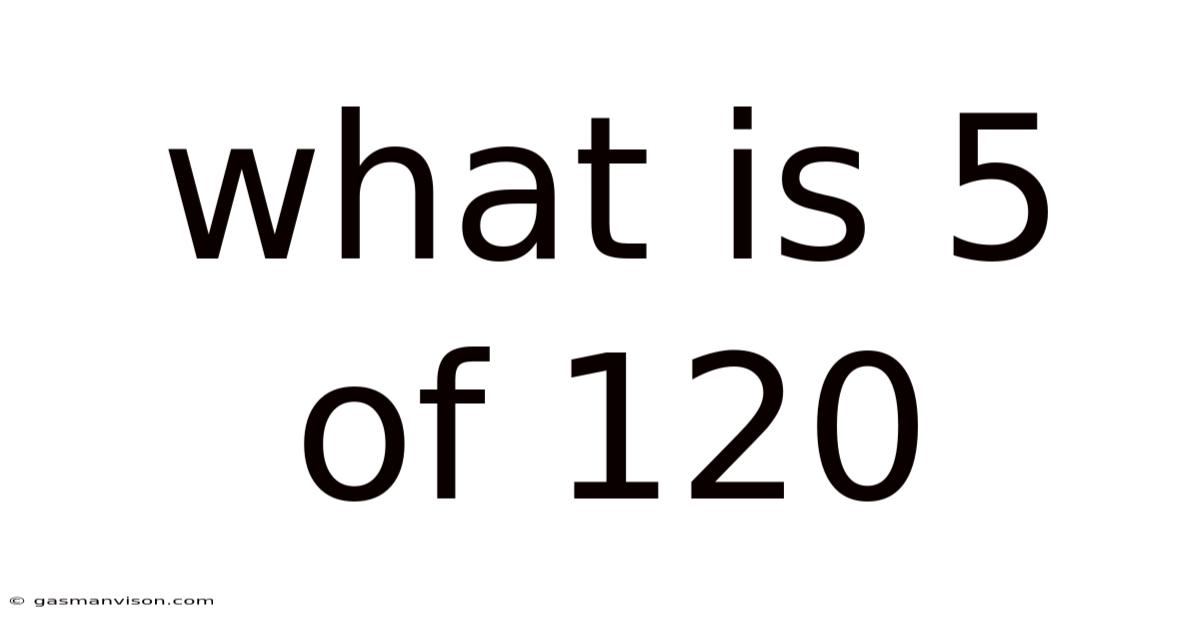
Table of Contents
What is 5% of 120? A Deep Dive into Percentages and Their Applications
Finding 5% of 120 might seem like a simple arithmetic problem, easily solvable with a calculator. However, understanding the underlying concepts of percentages and their diverse applications is crucial, not just for basic calculations but also for navigating complex scenarios in various fields like finance, statistics, and everyday life. This article will delve into calculating 5% of 120, explaining the methods involved and exploring the broader significance of percentage calculations. We'll also touch upon practical examples to illustrate the real-world relevance of this seemingly simple calculation.
Meta Description: Learn how to calculate 5% of 120 and understand the broader concepts of percentages, their applications in finance, statistics, and everyday life. This comprehensive guide covers various methods and real-world examples.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol used to represent percentage is '%'. Percentages are a convenient way to express proportions and comparisons, making them widely used in various contexts. For example, expressing a discount as 20% off is much clearer than saying "one-fifth off". Understanding percentages is fundamental to comprehending various aspects of the world around us.
Method 1: Using the Decimal Equivalent
The most straightforward way to calculate 5% of 120 is by converting the percentage to its decimal equivalent. To do this, divide the percentage by 100. Therefore, 5% becomes 5/100 = 0.05. Then, multiply this decimal by the number you're finding the percentage of:
0.05 * 120 = 6
Therefore, 5% of 120 is 6.
This method is efficient and easily adaptable to different percentages. Simply convert the percentage to a decimal and multiply it by the given number.
Method 2: Using Fractions
Another approach is to express the percentage as a fraction. 5% can be written as 5/100. This fraction can be simplified to 1/20. Then, multiply this fraction by 120:
(1/20) * 120 = 120/20 = 6
This method provides a different perspective on the calculation, illustrating the relationship between percentages, fractions, and whole numbers. This is particularly useful when dealing with percentages that have easily simplified fractions.
Method 3: Proportion Method
The proportion method leverages the concept of ratios to solve percentage problems. We can set up a proportion:
5/100 = x/120
Here, 'x' represents the unknown value (5% of 120). To solve for 'x', cross-multiply:
100x = 5 * 120 100x = 600 x = 600/100 x = 6
This method is particularly helpful in understanding the underlying relationship between the percentage and the whole number. It's a more formal approach, suitable for demonstrating the logical steps involved in percentage calculations.
Real-World Applications of Percentage Calculations
The seemingly simple calculation of 5% of 120 has far-reaching applications in various real-world scenarios. Here are a few examples:
-
Finance: Calculating interest on loans or savings accounts. Imagine you have a savings account with a 5% annual interest rate and a balance of $120. Using our calculation, you would earn $6 in interest after one year. This extends to calculating discounts, taxes, profit margins, and more. Understanding percentage calculations is fundamental to managing personal finances effectively.
-
Sales and Marketing: Determining discounts and price reductions. A store might offer a 5% discount on an item priced at $120. Using the calculation, the discount would be $6, resulting in a final price of $114. This principle extends to calculating sales tax, markups, and other crucial aspects of sales and marketing.
-
Statistics: Representing data as percentages in reports and analyses. For instance, if 5 out of 120 respondents chose a particular option in a survey, this represents 5% of the total respondents. Understanding percentages is essential for interpreting and presenting statistical data effectively.
-
Science and Engineering: Expressing concentration levels, efficiency rates, or error margins. Percentages are frequently used in scientific and engineering fields to express proportions and ratios accurately.
-
Everyday Life: Tip calculations, splitting bills, and understanding nutritional information. From calculating the tip at a restaurant to figuring out how much each person owes when splitting a bill, percentage calculations are an integral part of our daily lives. Even understanding the percentage of daily recommended values of nutrients on food labels involves percentage calculations.
Advanced Percentage Calculations
While calculating 5% of 120 is relatively straightforward, the core concepts extend to more complex percentage calculations. These include:
-
Calculating the percentage increase or decrease: This involves comparing two values and expressing the change as a percentage. For example, if a price increases from $100 to $120, the percentage increase is 20%.
-
Finding the original value given a percentage and the final value: This is the reverse calculation. If you know the final value after a 5% increase is $120, you can use algebraic equations to find the original value.
-
Calculating compound interest: This involves calculating interest not just on the principal amount, but also on accumulated interest. This is a crucial concept in finance and long-term investments.
Tips for Mastering Percentage Calculations
-
Practice regularly: The more you practice percentage calculations, the more comfortable you'll become with the different methods.
-
Use a calculator strategically: While calculators are helpful for complex calculations, understanding the underlying principles is crucial. Use the calculator to verify your results, not to replace your understanding.
-
Learn different methods: Different methods cater to various situations and preferences. Mastering multiple approaches allows you to select the most efficient method for the task at hand.
-
Understand the context: Always consider the context of the problem. This helps in interpreting the results and ensuring accuracy.
Conclusion: Beyond the Simple Calculation
While calculating 5% of 120 might appear simple, understanding the underlying principles of percentage calculations is essential for numerous applications. From personal finance to advanced scientific analysis, the ability to perform these calculations accurately and efficiently is a valuable skill. This article aims to provide not only the solution to the simple calculation but also a deeper understanding of the concepts and applications of percentages, empowering you to handle more complex percentage problems with confidence. The key takeaway is that mastering percentages is not merely about solving equations; it's about acquiring a fundamental skill that enhances your ability to navigate the quantitative aspects of the world around you.
Latest Posts
Latest Posts
-
Biotic Factors In A Ocean
Sep 24, 2025
-
18 Out Of 22 Percentage
Sep 24, 2025
-
Alka Seltzer Water Chemical Equation
Sep 24, 2025
-
What Is 15 Of 24
Sep 24, 2025
-
Dark Wood That Neutralizes Poison
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.