What Is 50 Of 16
gasmanvison
Sep 22, 2025 · 5 min read
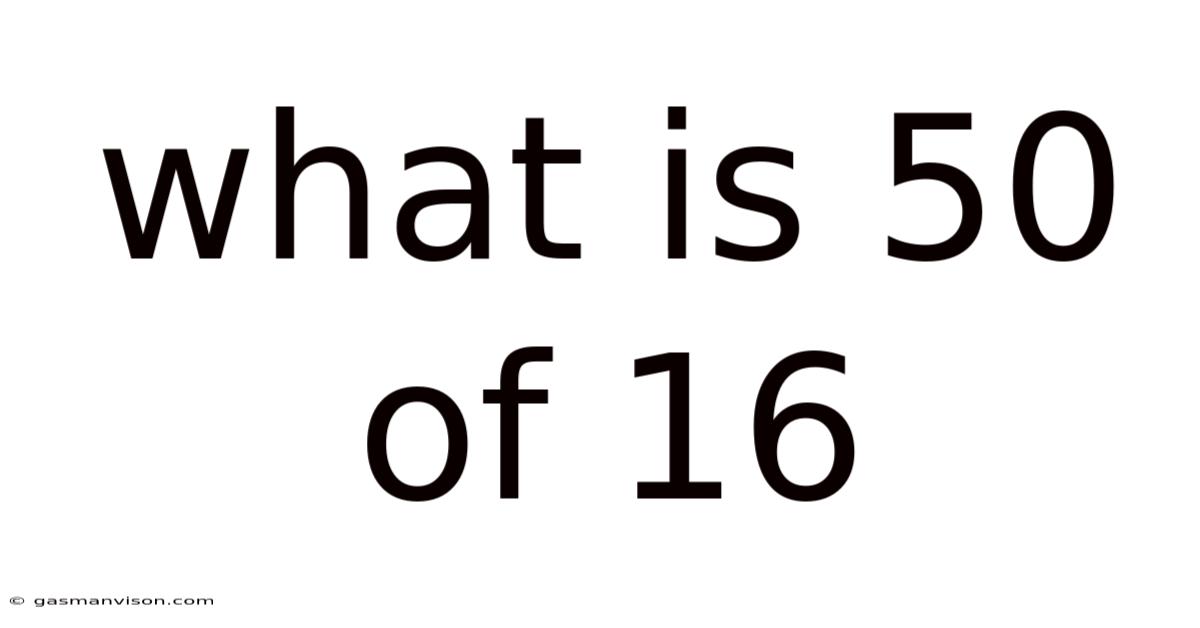
Table of Contents
What is 50% of 16? A Deep Dive into Percentages and Their Applications
Finding 50% of 16 might seem like a simple arithmetic problem, easily solved with a quick calculation. But this seemingly straightforward question opens the door to a broader understanding of percentages, their practical applications, and the various methods for calculating them. This article will delve into the solution, explore the underlying concepts, and showcase the versatility of percentage calculations in diverse fields. We'll uncover why understanding percentages is crucial, not just for mathematical proficiency, but also for navigating everyday life and making informed decisions.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" – "per cent" being a shortened form of "per centum," Latin for "out of one hundred." Therefore, 50% represents 50 parts out of a total of 100 parts. This fundamental concept forms the basis for all percentage calculations.
Calculating 50% of 16: Three Simple Methods
There are several ways to calculate 50% of 16. Here are three common approaches:
1. The Fraction Method:
Since 50% is equivalent to the fraction ½ (50/100 simplifies to 1/2), finding 50% of 16 is the same as finding half of 16. Simply divide 16 by 2:
16 ÷ 2 = 8
Therefore, 50% of 16 is 8.
2. The Decimal Method:
Percentages can also be expressed as decimals. To convert a percentage to a decimal, divide the percentage by 100. Thus, 50% becomes 0.50 (or simply 0.5). Multiplying this decimal by the original number gives us the answer:
16 x 0.5 = 8
This method is particularly useful when dealing with percentages that aren't easily represented as simple fractions.
3. The Proportion Method:
This method utilizes the concept of proportions. We can set up a proportion to solve for the unknown value (x):
50/100 = x/16
Cross-multiplying gives us:
100x = 50 * 16
100x = 800
x = 800/100
x = 8
This method, while slightly more involved, demonstrates the underlying proportional relationship between percentages and their corresponding values.
Beyond the Basics: Expanding Our Understanding of Percentages
While calculating 50% of 16 is straightforward, the true value of understanding percentages lies in their application to more complex scenarios. Let's explore some real-world examples:
1. Financial Calculations:
- Interest Rates: Understanding percentages is essential for calculating interest earned on savings accounts or interest paid on loans. Interest rates are typically expressed as percentages.
- Discounts: Sales and discounts are often advertised as percentages off the original price. Knowing how to calculate these discounts is crucial for savvy shopping.
- Taxes: Sales tax, income tax, and other taxes are expressed as percentages of the purchase price or income.
- Investment Returns: Tracking investment returns and understanding growth rates involves calculating percentage changes over time.
2. Data Analysis and Statistics:
- Representing Data: Percentages are frequently used to represent data visually using pie charts, bar graphs, and other visual aids.
- Statistical Analysis: Many statistical calculations, such as calculating percentages, standard deviations, and confidence intervals, rely heavily on understanding percentages.
- Surveys and Polls: Results from surveys and polls are often presented as percentages to represent the proportion of respondents holding specific opinions.
3. Science and Engineering:
- Measurement and Conversions: Percentages play a crucial role in converting units of measurement and expressing quantities relative to a whole.
- Error Analysis: In scientific experiments, percentages are used to express the margin of error in measurements.
- Chemical Concentrations: Concentrations of solutions and mixtures are often expressed as percentages (e.g., percentage by weight or volume).
4. Everyday Life:
- Tipping: Calculating tips in restaurants involves determining a percentage of the bill total.
- Cooking and Baking: Recipes often call for percentages of specific ingredients to ensure consistent results.
- Grading Systems: Academic grading systems frequently utilize percentages to express student performance.
Advanced Percentage Calculations: Tackling More Complex Problems
While finding 50% of 16 is a simple exercise, many situations require more complex percentage calculations. Let's consider some examples:
-
Calculating Percentage Increase/Decrease: This involves determining the percentage change between two values. For example, if a price increases from $10 to $12, the percentage increase is calculated as: [(12-10)/10] * 100% = 20%.
-
Finding the Original Value After a Percentage Change: If a price has been reduced by 20% to $8, we can find the original price using the following calculation: $8 / (1 - 0.20) = $10.
-
Calculating Percentage Points: This refers to the arithmetic difference between two percentages. For instance, if an interest rate increases from 5% to 8%, the increase is 3 percentage points, not 60% (which would be the percentage increase).
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest from previous periods. Compound interest calculations require a more advanced understanding of exponential growth.
Mastering Percentages: Tips and Techniques
To master percentage calculations and their applications, consider these tips:
- Practice Regularly: Regular practice is key to building proficiency in percentage calculations. Solve a variety of problems to reinforce your understanding.
- Understand the Underlying Concepts: Don't just memorize formulas; understand the underlying concepts of fractions, decimals, and proportions.
- Use Multiple Methods: Experiment with different methods to find the approach that best suits your understanding and the specific problem at hand.
- Utilize Calculators and Software: While understanding the fundamental principles is crucial, calculators and spreadsheet software can significantly streamline the calculation process for complex problems.
- Break Down Complex Problems: Decompose complex problems into smaller, more manageable steps.
Conclusion: The Importance of Percentage Proficiency
In conclusion, while the answer to "What is 50% of 16?" is a simple 8, the journey to reach that answer highlights the broader importance of understanding percentages. From financial management and data analysis to scientific research and everyday life decisions, proficiency in percentage calculations is a valuable skill that empowers informed decision-making and a deeper understanding of the quantitative world around us. The seemingly simple act of calculating 50% of 16 serves as a gateway to a wealth of applications and opportunities for growth in numerical literacy. By mastering percentages, you equip yourself with a powerful tool for navigating a complex and data-driven world.
Latest Posts
Latest Posts
-
Maletas Ser Pasajero
Sep 22, 2025
-
Group 6a On Periodic Table
Sep 22, 2025
-
Fly Like The Wind Meaning
Sep 22, 2025
-
31 Billion In Scientific Notation
Sep 22, 2025
-
How Much Is 3 Nickels
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 50 Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.