What Is 50 Of 300
gasmanvison
Sep 20, 2025 · 5 min read
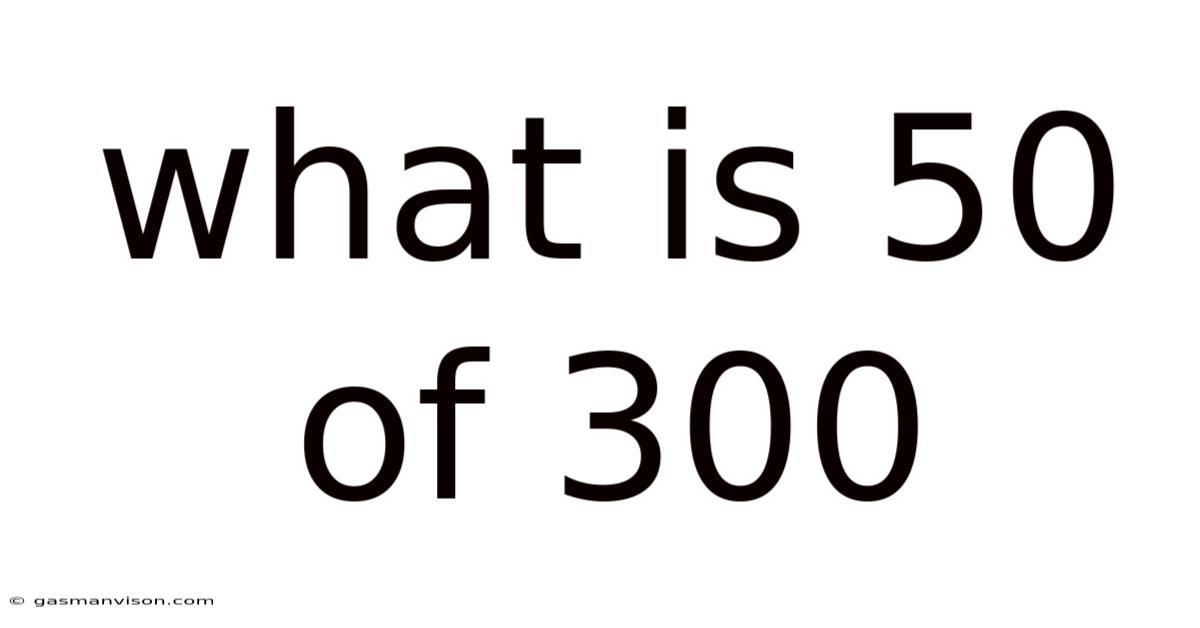
Table of Contents
What is 50% of 300? A Comprehensive Guide to Percentages and Their Applications
Finding 50% of 300 is a simple percentage calculation, but understanding the underlying principles allows you to tackle more complex percentage problems. This article will not only answer the question directly but also delve into the various methods for calculating percentages, their real-world applications, and how to improve your understanding of this fundamental mathematical concept. This guide is designed for everyone, from students brushing up on their math skills to professionals needing a refresher on percentage calculations for business or finance.
What is 50% of 300? The Answer and the Method
The answer to "What is 50% of 300?" is 150. This is because 50% represents one-half (50/100 = 1/2), and half of 300 is 150. We can calculate this in several ways:
Method 1: Using Fractions
- Convert the percentage to a fraction: 50% is equivalent to 50/100, which simplifies to 1/2.
- Multiply the fraction by the number: (1/2) * 300 = 150
Method 2: Using Decimal Equivalents
- Convert the percentage to a decimal: 50% is equivalent to 0.5 (divide the percentage by 100).
- Multiply the decimal by the number: 0.5 * 300 = 150
Method 3: Using the Percentage Formula
The basic percentage formula is: (Percentage/100) * Number = Result
Substituting the values: (50/100) * 300 = 150
Beyond the Basics: Understanding Percentages More Deeply
While finding 50% of 300 is straightforward, a deeper understanding of percentages is crucial for various aspects of life. Let's explore some key concepts:
What are Percentages?
Percentages are a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin "per centum," meaning "out of a hundred." Percentages are used extensively to represent proportions, rates, and changes in various fields.
Types of Percentage Problems
There are several types of percentage problems you might encounter:
- Finding a percentage of a number: This is the type of problem we just solved (finding 50% of 300).
- Finding what percentage one number is of another: For example, what percentage of 300 is 150? (The answer is 50%).
- Finding the original number when a percentage is known: For example, if 20% of a number is 60, what is the number? (The answer is 300).
- Calculating percentage increase or decrease: This involves finding the percentage change between two numbers.
Real-World Applications of Percentages
Percentages are used in countless real-world situations, including:
- Finance: Calculating interest rates, discounts, taxes, profits, and losses. Understanding percentages is essential for managing personal finances, investing, and understanding financial reports. For example, calculating the interest on a loan or the return on investment relies heavily on percentage calculations.
- Business: Analyzing sales figures, market share, profit margins, and growth rates. Business decisions are often driven by data analysis that relies heavily on understanding percentage changes and trends. For instance, tracking the percentage increase in sales year-over-year can inform marketing strategies.
- Science: Representing experimental data, statistical analysis, and probability. In scientific research, percentages are used to express the proportion of a sample that exhibits a certain characteristic, or to present the likelihood of a particular outcome.
- Everyday Life: Calculating tips, discounts in stores, understanding nutritional information on food labels, and interpreting statistics in news reports. From figuring out the tip at a restaurant to understanding the percentage of fat in a food product, percentages are integrated into daily life.
Tips for Solving Percentage Problems
Here are some helpful tips to improve your accuracy and efficiency when dealing with percentages:
- Understand the Basics: Make sure you understand the fundamental concepts of fractions, decimals, and proportions before tackling more complex percentage problems.
- Use a Calculator: Calculators can significantly simplify percentage calculations, especially when dealing with larger numbers or more complex problems.
- Break Down Complex Problems: Divide complex problems into smaller, manageable steps. This approach reduces the chances of making errors.
- Check Your Work: Always double-check your calculations to ensure accuracy. One common error is misplacing the decimal point.
- Practice Regularly: The best way to improve your understanding and skills is through consistent practice.
Advanced Percentage Calculations and Applications
Let's explore some more advanced concepts and applications of percentage calculations:
Compound Interest
Compound interest is interest earned on both the principal amount and accumulated interest. This means that the interest earned in each period is added to the principal, and the subsequent interest calculation is based on the increased amount. Understanding compound interest is crucial for long-term investments and financial planning. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Percentage Change
Percentage change is used to express the relative difference between an old and a new value. It's calculated as:
[(New Value - Old Value) / Old Value] * 100%
A positive result indicates an increase, while a negative result indicates a decrease. This is used extensively in business, finance, and economics to analyze trends and growth rates. For instance, comparing sales figures from one year to the next involves calculating the percentage change.
Percentage Points
It is important to distinguish between percentage change and percentage points. Percentage points refer to the arithmetic difference between two percentages. For example, if interest rates increase from 5% to 8%, the increase is 3 percentage points, not a 60% increase (calculated as percentage change).
Conclusion
This comprehensive guide has covered the basics and advanced aspects of percentage calculations, starting with the simple answer to "What is 50% of 300?" and moving to more complex scenarios. Understanding percentages is a valuable skill applicable to various fields, from personal finance to scientific research. Mastering these concepts and practicing regularly will greatly improve your numerical literacy and problem-solving abilities. Remember to utilize the different methods provided and to always check your work to ensure accuracy. With consistent practice and a firm grasp of the underlying principles, you can confidently tackle any percentage-related problem.
Latest Posts
Latest Posts
-
Ddt Has Been Found To
Sep 20, 2025
-
Bipolar Neurons Are Commonly
Sep 20, 2025
-
How Much Is 77 Kg
Sep 20, 2025
-
Formula For Copper 2 Phosphate
Sep 20, 2025
-
Which Statement Best Describes Engraving
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 50 Of 300 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.