What Is 55 Of 125
gasmanvison
Sep 24, 2025 · 4 min read
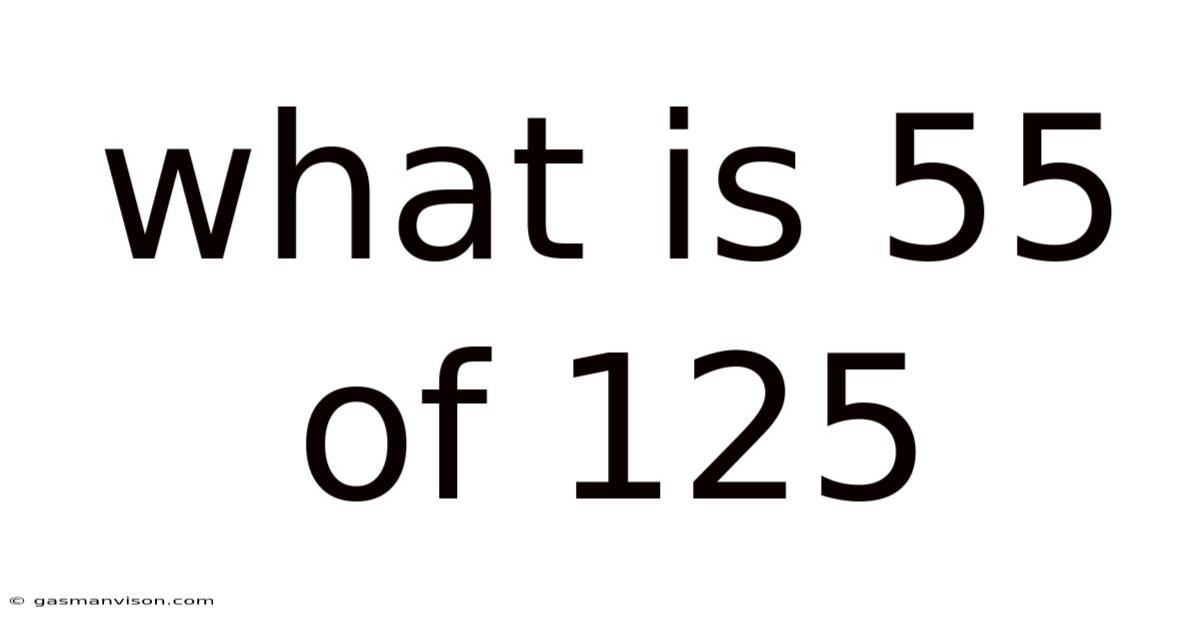
Table of Contents
What is 55% of 125? A Comprehensive Guide to Percentage Calculations
Finding the percentage of a number is a fundamental mathematical skill applicable in various everyday situations, from calculating discounts and sales tax to understanding statistical data and financial reports. This article will delve into calculating "What is 55% of 125?" We'll not only provide the answer but also explore different methods for solving percentage problems, ensuring you understand the underlying concepts and can confidently tackle similar calculations in the future. This guide is designed to be beginner-friendly, progressively introducing more advanced techniques.
Understanding Percentages:
A percentage is a fraction expressed as a number out of 100. The symbol "%" represents "per hundred". So, 55% means 55 out of 100, or 55/100. Understanding this fundamental concept is crucial for any percentage calculation.
Method 1: Using the Decimal Equivalent
The most straightforward method involves converting the percentage to its decimal equivalent. To do this, divide the percentage by 100.
-
Step 1: Convert the percentage to a decimal: 55% / 100 = 0.55
-
Step 2: Multiply the decimal by the number: 0.55 * 125 = 68.75
Therefore, 55% of 125 is 68.75.
This method is efficient and readily applicable to most percentage calculations using a calculator.
Method 2: Using Fractions
This method leverages the fractional representation of percentages.
-
Step 1: Express the percentage as a fraction: 55% = 55/100
-
Step 2: Simplify the fraction (if possible): 55/100 can be simplified to 11/20
-
Step 3: Multiply the fraction by the number: (11/20) * 125
-
Step 4: Simplify and calculate: (11/20) * 125 = (11 * 125) / 20 = 1375 / 20 = 68.75
This method offers a deeper understanding of the underlying mathematical principles, but it might be slightly more time-consuming than the decimal method, especially with more complex fractions.
Method 3: Using Proportions
This method uses the concept of proportions to solve for the unknown value. We can set up a proportion:
-
Step 1: Set up the proportion: x/125 = 55/100 (where 'x' represents 55% of 125)
-
Step 2: Cross-multiply: 100x = 55 * 125
-
Step 3: Solve for x: 100x = 6875 => x = 6875 / 100 = 68.75
This method is particularly useful when dealing with more complex percentage problems or when visualizing the relationship between the percentage and the whole number.
Real-World Applications of Percentage Calculations:
Understanding percentage calculations is crucial for numerous everyday scenarios:
-
Retail Discounts: Calculating discounts on sale items. For example, a 20% discount on a $100 item would be 20/100 * $100 = $20.
-
Sales Tax: Determining the total cost of an item including sales tax. For instance, a 6% sales tax on a $50 item is 6/100 * $50 = $3.
-
Interest Calculations: Calculating simple or compound interest on loans or investments.
-
Grade Calculation: Determining your final grade in a course based on different assignment weights and scores.
-
Tip Calculation: Calculating the appropriate tip amount in a restaurant.
-
Data Analysis: Interpreting statistical data presented as percentages, such as survey results or market share.
Advanced Percentage Calculations:
While the methods discussed above cover basic percentage calculations, several other scenarios require more advanced techniques:
-
Finding the Percentage Increase or Decrease: This involves calculating the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] * 100.
-
Finding the Original Value: If you know the percentage and the resulting value after a percentage increase or decrease, you can work backward to find the original value.
-
Calculating Percentage Points: Percentage points represent the absolute difference between two percentages, not the relative change. For example, an increase from 10% to 20% is a 10 percentage point increase, but a 100% relative increase.
-
Compound Percentage Growth: This involves calculating the accumulated growth over multiple periods, where the growth in each period is added to the principal amount before calculating the growth for the next period.
Tips and Tricks for Efficient Percentage Calculations:
-
Memorize common percentage equivalents: Knowing that 10% is 0.1, 25% is 0.25, and 50% is 0.5 can significantly speed up calculations.
-
Use a calculator effectively: Calculators are valuable tools for handling percentage calculations, particularly those involving decimals or fractions.
-
Break down complex problems: For complex percentage problems, break them down into smaller, more manageable steps.
-
Check your work: Always double-check your calculations to ensure accuracy.
Conclusion:
Calculating percentages is a fundamental skill with broad applicability. Understanding the different methods—using decimal equivalents, fractions, and proportions—provides flexibility and a deeper understanding of the underlying mathematical principles. By mastering these methods and practicing regularly, you'll confidently handle various percentage problems encountered in your daily life and academic or professional pursuits. Remember to apply these methods strategically depending on the context and complexity of the problem at hand. The ability to perform accurate and efficient percentage calculations is a valuable asset in various aspects of life.
Latest Posts
Latest Posts
-
Baking Soda Homogeneous Or Heterogeneous
Sep 24, 2025
-
Cumulative Exam Cumulative Exam Review
Sep 24, 2025
-
37 5 Degrees Celsius To Fahrenheit
Sep 24, 2025
-
Chorine And Lithium Ionic Compound
Sep 24, 2025
-
Biotic Factors In A Ocean
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 55 Of 125 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.