What Is 70 Of 90
gasmanvison
Sep 06, 2025 · 5 min read
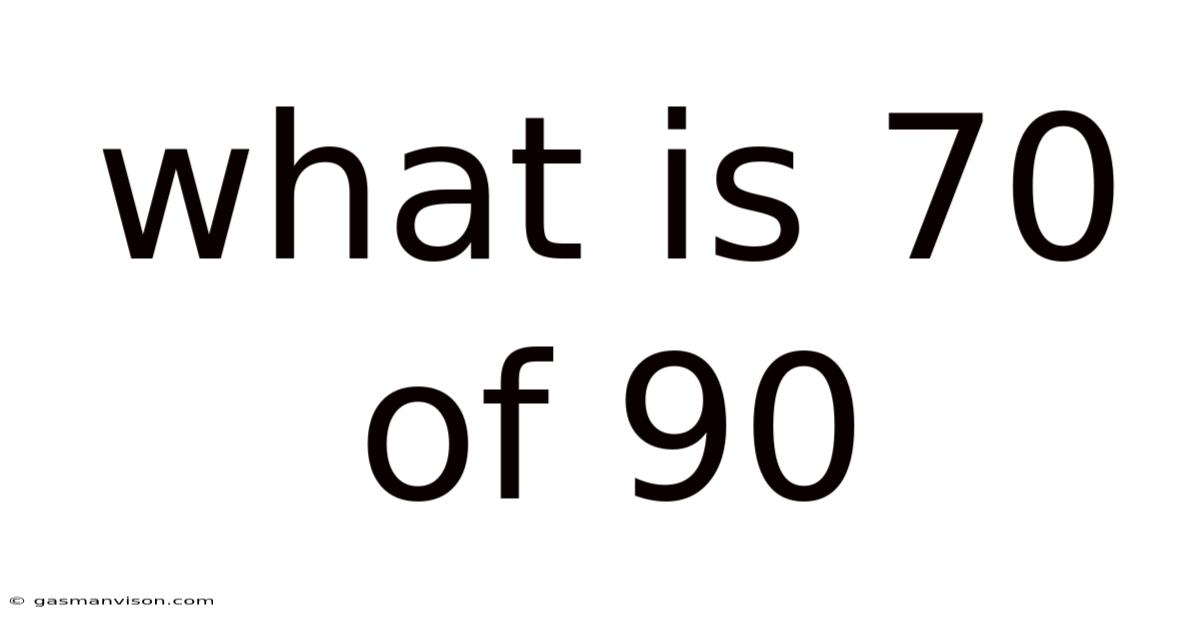
Table of Contents
What is 70% of 90? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "What is 70% of 90?", opens a door to understanding percentages, a fundamental concept in mathematics with widespread applications in daily life and various professional fields. This article will not only answer the question directly but also delve into the methods for calculating percentages, explore their real-world applications, and provide practical tips for mastering percentage calculations. Understanding percentages is crucial for budgeting, finance, sales, statistics, and many other areas. Let's dive in!
Understanding Percentages: The Basics
A percentage is a fraction or a ratio expressed as a number out of 100. The symbol "%" represents "percent," meaning "per hundred." Therefore, 70% means 70 out of 100, which can also be written as the fraction 70/100 or the decimal 0.70. This foundational understanding is key to solving percentage problems.
Method 1: Using the Formula
The most straightforward method to calculate 70% of 90 involves using the basic percentage formula:
Part = Percentage × Whole
In this case:
- Part: This is the value we want to find – 70% of 90.
- Percentage: This is 70%, which we convert to a decimal by dividing by 100 (70/100 = 0.70).
- Whole: This is the total value, which is 90.
Therefore, the calculation is:
Part = 0.70 × 90 = 63
So, 70% of 90 is 63.
Method 2: Using Fractions
Percentages can also be expressed as fractions. 70% can be written as 70/100, which simplifies to 7/10. To find 70% of 90 using fractions, we multiply the fraction by the whole number:
(7/10) × 90 = 630/10 = 63
This method demonstrates the equivalence between fractions and percentages and offers an alternative approach to the calculation.
Method 3: Using Proportions
The concept of proportions provides another effective way to solve percentage problems. A proportion is a statement of equality between two ratios. We can set up a proportion to find 70% of 90:
70/100 = x/90
To solve for x (which represents 70% of 90), we cross-multiply:
70 × 90 = 100 × x
6300 = 100x
x = 6300/100 = 63
This method highlights the relationship between percentages and ratios, offering a more algebraic approach.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous aspects of daily life and various professions. Here are some examples:
-
Finance: Calculating interest on loans, savings accounts, and investments heavily relies on percentages. Understanding interest rates and their impact on your finances is crucial for making informed financial decisions. For example, calculating the interest earned on a savings account or the total cost of a loan after interest is accrued.
-
Sales and Discounts: Retail stores frequently offer discounts expressed as percentages. Being able to quickly calculate the discounted price is essential for savvy shoppers. For instance, a 20% discount on a $100 item means a saving of $20, resulting in a final price of $80.
-
Taxes: Sales tax, income tax, and property tax are all calculated as percentages of the taxable amount. Understanding tax rates allows individuals and businesses to accurately estimate their tax obligations.
-
Statistics and Data Analysis: Percentages are widely used to represent proportions and trends in data. Surveys, polls, and research studies often express results using percentages to make the data easier to understand and interpret. For example, understanding market share percentages in business or the percentage of a population with a specific characteristic.
-
Science and Engineering: Percentages are used extensively in scientific calculations, such as expressing concentrations of solutions, efficiency rates of machines, or error margins in experiments.
-
Everyday Life: Calculating tips in restaurants, figuring out the percentage of a certain ingredient in a recipe, or determining the amount of discount you’ll receive on a sale are all examples of daily applications.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: The key to mastering any mathematical concept is consistent practice. Solve various percentage problems, starting with simple ones and gradually increasing the complexity.
-
Understand the Formula: Thoroughly understand the underlying formula (Part = Percentage × Whole) and its variations.
-
Convert Percentages to Decimals or Fractions: Converting percentages to decimals or fractions simplifies the calculation process.
-
Use a Calculator: For more complex calculations, using a calculator can save time and ensure accuracy. However, try to solve the problems manually first to strengthen your understanding.
-
Check Your Work: Always double-check your calculations to ensure accuracy. You can use different methods to verify your answer.
-
Learn Mental Math Techniques: Practice mental math techniques to quickly estimate percentages. For instance, 10% of a number is simply moving the decimal point one place to the left.
-
Utilize Online Resources: Several online calculators and tutorials can help you practice and improve your understanding of percentages.
Beyond the Basic Calculation: Exploring More Complex Percentage Problems
While this article primarily focused on finding a simple percentage of a number, the principles discussed can be applied to a wider range of percentage problems, including:
-
Finding the percentage increase or decrease: This involves calculating the percentage change between two values.
-
Finding the original value before a percentage change: This is the reverse of calculating a percentage increase or decrease.
-
Calculating percentage points: This is different from a percentage change and represents the absolute difference between two percentages.
-
Working with compound interest: This involves calculating interest on both the principal amount and the accumulated interest.
Conclusion
The answer to "What is 70% of 90?" is 63. However, the true value of this seemingly simple question lies in understanding the broader context of percentage calculations. Mastering percentages is a valuable skill that extends far beyond the classroom, impacting various aspects of daily life and professional endeavors. By understanding the different methods of calculation, practicing regularly, and applying these principles to real-world scenarios, you can confidently tackle percentage problems and enhance your mathematical proficiency. Remember, practice is key to becoming proficient in percentage calculations, and the rewards are well worth the effort.
Latest Posts
Latest Posts
-
5 To The 4th Power
Sep 06, 2025
-
What Happens During Prophase 1
Sep 06, 2025
-
El Hijo De Mi Hermano
Sep 06, 2025
-
10 Grams How Many Ounces
Sep 06, 2025
-
How Does A Barometer Work
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about What Is 70 Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.