What Is 75 Of 150
gasmanvison
Sep 11, 2025 · 5 min read
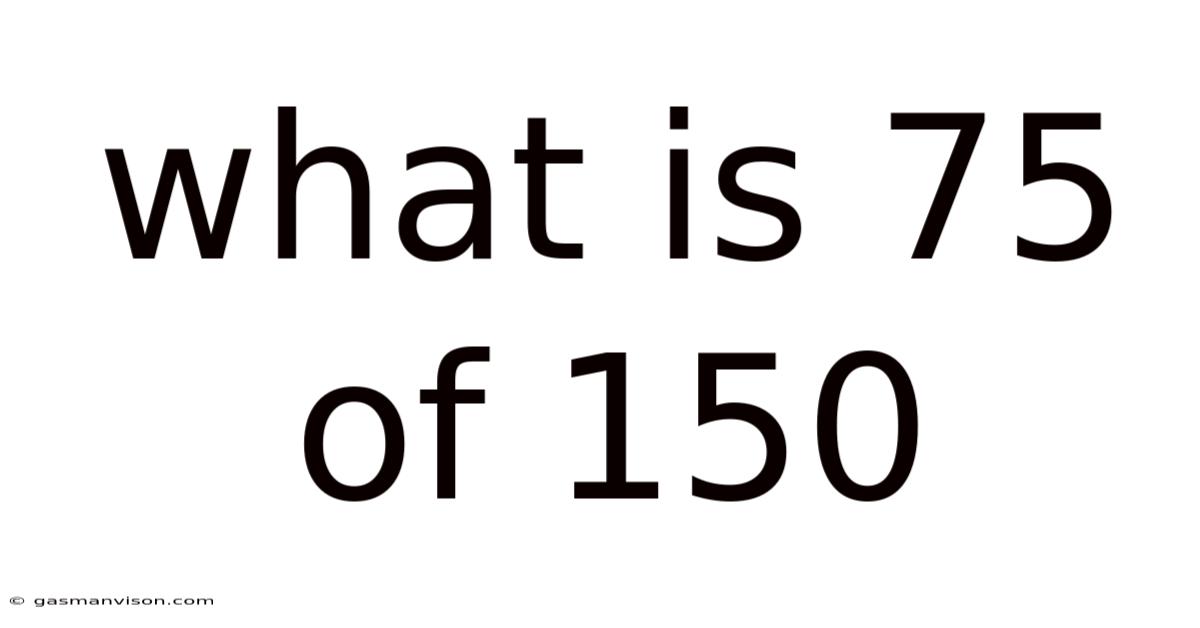
Table of Contents
What is 75% of 150? A Comprehensive Guide to Percentages and Their Applications
Finding 75% of 150 might seem like a simple arithmetic problem, but understanding the underlying concepts of percentages and their diverse applications is crucial for navigating various aspects of life, from finance and shopping to data analysis and academic studies. This article delves deep into the calculation of 75% of 150, explaining the process in detail and exploring the broader significance of percentage calculations. We will also look at different methods to solve this problem and provide real-world examples to illustrate its practical application.
Meta Description: Learn how to calculate 75% of 150 and understand the broader concept of percentages. This comprehensive guide explores various methods, real-world applications, and the importance of percentage calculations in everyday life.
Understanding Percentages: The Foundation of Calculation
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." Therefore, 75% can be understood as 75 parts out of 100, or 75/100. This fractional representation is key to understanding how percentages work. This fundamental concept allows us to easily compare proportions and ratios across different quantities. Mastering percentages is essential for countless applications, from calculating discounts and taxes to understanding statistical data and financial reports.
Method 1: Converting Percentage to Decimal
This is arguably the most straightforward method. To find 75% of 150, we first convert the percentage to its decimal equivalent. We do this by dividing the percentage by 100.
75% ÷ 100 = 0.75
Now, we multiply this decimal by the number we want to find the percentage of:
0.75 x 150 = 112.5
Therefore, 75% of 150 is 112.5.
Method 2: Using Fractions
As mentioned earlier, percentages can be expressed as fractions. 75% can be written as 75/100. This fraction can be simplified:
75/100 = 3/4
Now we multiply this simplified fraction by 150:
(3/4) x 150 = (3 x 150) / 4 = 450 / 4 = 112.5
Again, we find that 75% of 150 is 112.5. This method demonstrates the interconnectedness of fractions, decimals, and percentages.
Method 3: Proportion Method
This method utilizes the concept of ratios and proportions. We can set up a proportion to solve for the unknown value:
75/100 = x/150
To solve for x (which represents 75% of 150), we cross-multiply:
75 x 150 = 100 x x
11250 = 100x
x = 11250 / 100
x = 112.5
This method reinforces the understanding of proportional relationships and provides an alternative approach to solving percentage problems.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a valuable skill applicable across numerous scenarios:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For example, understanding a 75% off sale requires this skill to determine the final price of an item.
-
Shopping: Determining the final price after a discount, comparing prices from different stores, and calculating sales tax all involve percentage calculations. For example, if a product costs $150 and is discounted by 25%, calculating the final price depends on understanding percentages.
-
Data Analysis: Interpreting statistical data often requires understanding percentages. Percentages are frequently used to represent proportions and probabilities in charts, graphs, and reports. For example, understanding survey results often involves percentage representation.
-
Academic Studies: Percentages are extensively used in academic settings to represent grades, scores, and statistical data. Converting raw scores to percentages is a common practice in many academic disciplines.
-
Everyday Life: Calculating tips at restaurants, splitting bills, determining the percentage of a budget allocated to various expenses – these are all everyday scenarios where percentage calculations are needed.
Beyond the Basics: More Complex Percentage Problems
While calculating 75% of 150 is a relatively straightforward problem, the principles involved extend to more complex scenarios. For instance:
-
Finding the Percentage Increase or Decrease: Determining the percentage change between two values requires understanding how to calculate the difference between the values and then expressing that difference as a percentage of the original value.
-
Calculating Percentage Points: This refers to the arithmetic difference between two percentages, not a percentage change. For example, an increase from 25% to 50% is a 25 percentage point increase, not a 100% increase.
-
Compound Interest: This involves calculating interest on the principal amount plus accumulated interest from previous periods. It’s a more complex calculation involving exponential growth.
-
Percentage Markup and Markdown: Businesses use percentage markup to determine the selling price of a product based on the cost price, while markdown represents a percentage reduction in the selling price.
Practicing Percentage Calculations: Tips and Tricks
-
Master the Fundamentals: A strong understanding of fractions, decimals, and the concept of "per hundred" is crucial for success.
-
Use a Calculator: While mental calculations are useful, using a calculator can save time and improve accuracy, especially for complex problems.
-
Break Down Complex Problems: Large or multi-step problems can be simplified by breaking them down into smaller, manageable parts.
-
Check Your Work: Always double-check your calculations to ensure accuracy. Compare your answer using different methods to confirm its validity.
-
Practice Regularly: The more you practice percentage calculations, the more comfortable and proficient you will become.
Conclusion: The Importance of Percentage Mastery
In conclusion, while knowing that 75% of 150 is 112.5 is helpful, understanding the underlying principles of percentage calculations is far more valuable. This skill is a fundamental building block for success in various fields and everyday life. By mastering the different methods and appreciating the real-world applications, you equip yourself with a tool that greatly enhances your numerical literacy and problem-solving abilities. The ability to confidently and accurately work with percentages is a skill that will continue to serve you well throughout your life.
Latest Posts
Latest Posts
-
Molar Mass Of Barium Nitrate
Sep 11, 2025
-
Defensive Drivers Plan Ahead By
Sep 11, 2025
-
1 Ml To Mg Medicine
Sep 11, 2025
-
How Long Is 33 Months
Sep 11, 2025
-
Ixl Special Right Triangles Answers
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.