What Is 75 Of 225
gasmanvison
Sep 05, 2025 · 5 min read
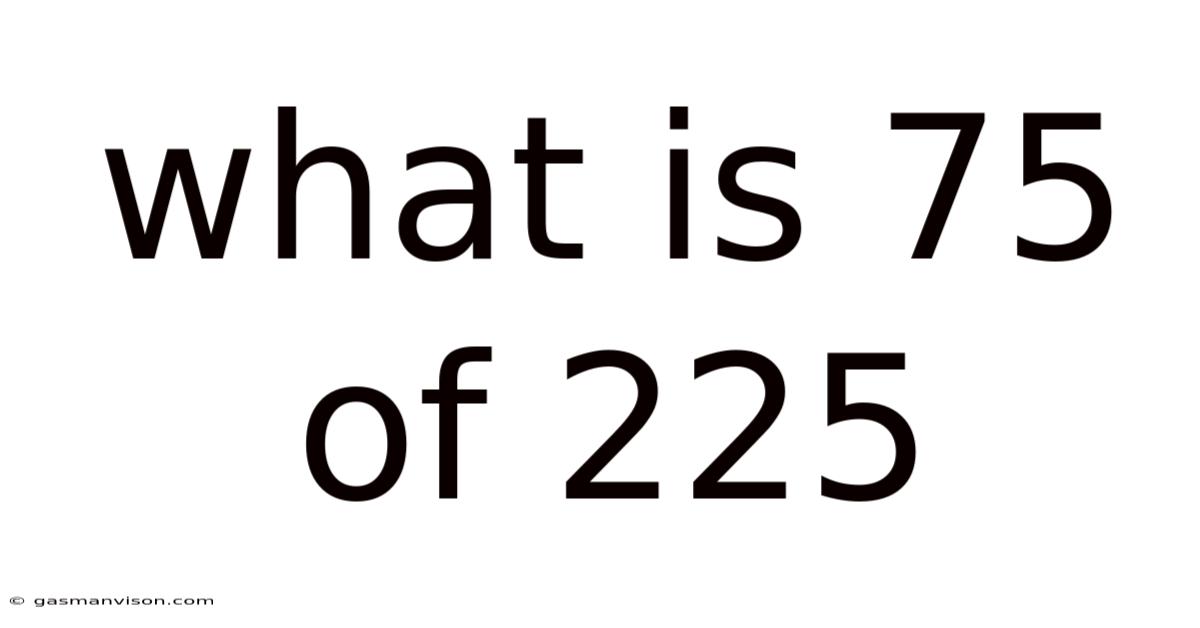
Table of Contents
What is 75% of 225? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 75% of 225?", opens the door to a broader understanding of percentages, their calculation, and their widespread applications in various fields. This article will not only answer the question directly but also explore the underlying concepts, different methods of calculation, and real-world examples to solidify your grasp of percentages. Understanding percentages is crucial for everyday life, from calculating discounts and taxes to analyzing data and making informed financial decisions.
Meta Description: Learn how to calculate 75% of 225 and master percentage calculations. This comprehensive guide explores different methods, real-world applications, and provides a deeper understanding of percentages.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol % represents "per cent," meaning "out of one hundred." For example, 75% means 75 out of 100, which can also be expressed as the fraction 75/100 or the decimal 0.75. Understanding this fundamental relationship is key to calculating percentages.
Method 1: Using Decimal Conversion
This is arguably the most straightforward method. We convert the percentage to its decimal equivalent and then multiply it by the given number.
-
Convert the percentage to a decimal: To convert 75% to a decimal, divide it by 100: 75 / 100 = 0.75
-
Multiply the decimal by the given number: Multiply 0.75 by 225: 0.75 * 225 = 168.75
Therefore, 75% of 225 is 168.75.
Method 2: Using Fractions
This method involves converting the percentage to a fraction and then performing the calculation.
-
Convert the percentage to a fraction: 75% can be written as 75/100. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 25: 75/100 = 3/4
-
Multiply the fraction by the given number: Multiply 3/4 by 225: (3/4) * 225 = (3 * 225) / 4 = 675 / 4 = 168.75
Again, 75% of 225 is 168.75.
Method 3: Using Proportions
This method uses the concept of ratios and proportions to solve the problem.
We can set up a proportion:
75/100 = x/225
where 'x' represents the unknown value (75% of 225).
To solve for x, we cross-multiply:
75 * 225 = 100 * x
16875 = 100x
x = 16875 / 100 = 168.75
Once again, 75% of 225 is 168.75.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in numerous real-world situations. Here are a few examples:
-
Sales and Discounts: Retail stores frequently offer discounts expressed as percentages. For example, a 25% discount on a $100 item means you save $25 (25% of $100). Calculating the final price after a discount involves subtracting the discount amount from the original price.
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages of the purchase price or income. Calculating the tax amount involves multiplying the tax rate by the taxable amount.
-
Interest Rates: Interest rates on loans, savings accounts, and investments are usually stated as percentages. Understanding compound interest, which involves calculating interest on the principal plus accumulated interest, requires proficiency in percentage calculations.
-
Tip Calculation: Calculating a tip in a restaurant often involves determining a percentage of the bill amount. A common tip is 15% or 20% of the total bill.
-
Data Analysis: Percentages are extensively used in data analysis to represent proportions, changes, and trends. For instance, analyzing market share, growth rates, or survey results frequently involves percentage calculations.
-
Grading Systems: Many educational institutions use percentage-based grading systems where a student's final grade is expressed as a percentage of the total possible points.
-
Financial Statements: Financial statements, such as income statements and balance sheets, often use percentages to present ratios and analyze financial performance. For example, profit margin is calculated as a percentage of revenue.
-
Statistical Analysis: Percentages are essential in statistical analysis for expressing probabilities, confidence intervals, and other statistical measures.
Beyond the Basics: More Complex Percentage Problems
While calculating 75% of 225 is relatively simple, the principles involved can be applied to more complex scenarios:
-
Finding the Percentage: Instead of finding a percentage of a number, you might need to find what percentage one number represents of another. For example, what percentage is 150 of 200? (Answer: 75%)
-
Finding the Original Value: You might know the percentage and the resulting value and need to find the original value. For example, if 20% of a number is 10, what is the original number? (Answer: 50)
-
Successive Percentages: You may need to apply multiple percentages successively. For example, if you have a 10% discount followed by a 5% discount, the final price will not simply be a 15% discount.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: The best way to master percentage calculations is through consistent practice. Work through various problems of increasing complexity.
-
Use a Calculator: While understanding the underlying principles is important, using a calculator can speed up the process, especially for more complex calculations.
-
Understand the Relationships: Remember the fundamental relationship between percentages, decimals, and fractions. This understanding will make calculations smoother and more intuitive.
-
Break Down Complex Problems: If you encounter a complex problem, try breaking it down into smaller, manageable steps.
-
Check Your Work: Always check your work to ensure accuracy.
Conclusion
This comprehensive guide not only answers the initial question – 75% of 225 is 168.75 – but also provides a deep dive into the world of percentage calculations. By understanding the different methods, their applications, and the tips for mastering them, you can confidently tackle percentage problems in various contexts, from everyday calculations to more advanced mathematical and financial scenarios. Remember that consistent practice is key to developing fluency and accuracy in handling percentages. The more you practice, the more intuitive and straightforward these calculations will become.
Latest Posts
Latest Posts
-
Susan Jones Npi Number Texas
Sep 07, 2025
-
Is 125 A Perfect Square
Sep 07, 2025
-
Breakaway Torque Is Affected By
Sep 07, 2025
-
Jarl Makes Several Minor Mistakes
Sep 07, 2025
-
Which Clause Defines Total Disability
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Of 225 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.