What Is 75 Of 250
gasmanvison
Sep 25, 2025 · 5 min read
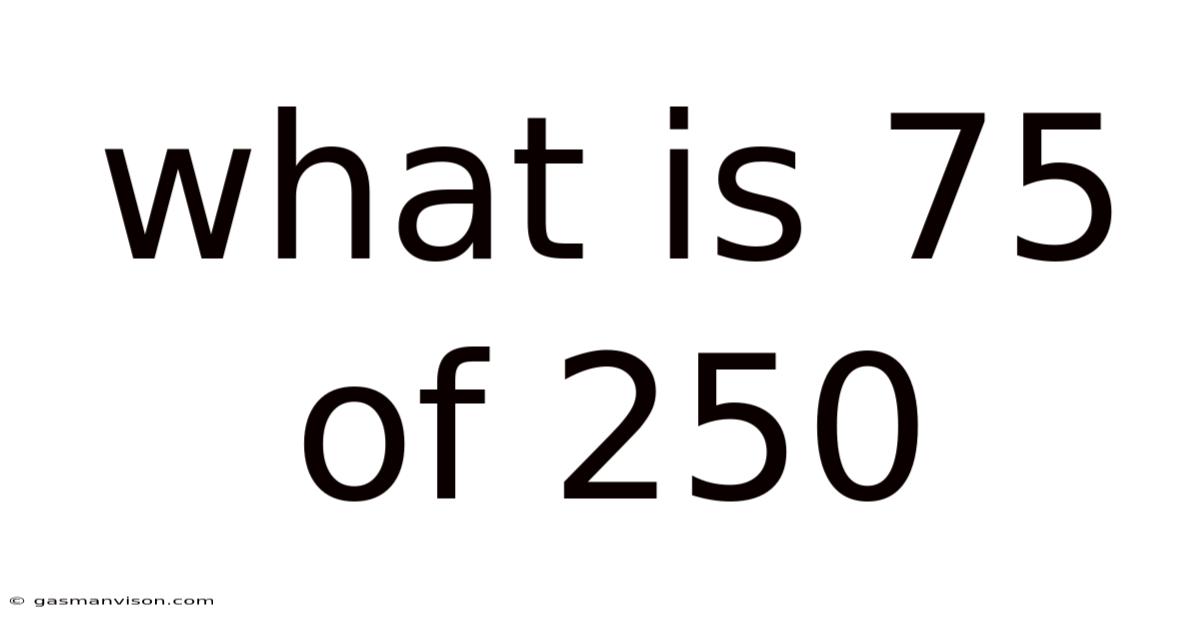
Table of Contents
What is 75% of 250? A Comprehensive Guide to Percentage Calculations
Finding a percentage of a number is a fundamental mathematical skill with widespread applications in everyday life, from calculating discounts and sales tax to understanding statistics and financial data. This article will thoroughly explore how to calculate 75% of 250, providing multiple methods and explaining the underlying concepts. We'll also delve into the practical applications of percentage calculations and offer resources for further learning. This guide is designed to be accessible to all levels, from beginners needing a refresher to those seeking a deeper understanding of percentage calculations.
Meta Description: Learn how to calculate 75% of 250 using various methods. This comprehensive guide explains percentage calculations, provides practical examples, and explores real-world applications. Master percentage calculations today!
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent." Therefore, 75% means 75 out of 100, or 75/100. This fraction can be simplified to 3/4. Understanding this fundamental concept is crucial for tackling percentage calculations.
Method 1: Using the Fraction Method
This method leverages the fraction equivalent of the percentage. Since 75% is equivalent to 3/4, we can calculate 75% of 250 as follows:
(3/4) * 250 = 750/4 = 187.5
Therefore, 75% of 250 is 187.5.
This method is particularly useful when dealing with percentages that have simple fraction equivalents, like 25%, 50%, and 75%.
Method 2: Converting Percentage to Decimal
This is arguably the most common and versatile method for calculating percentages. To use this method, convert the percentage to its decimal equivalent by dividing by 100. 75% becomes 0.75 (75 ÷ 100 = 0.75). Then, multiply the decimal by the number:
0.75 * 250 = 187.5
This method is straightforward and easily adaptable to any percentage calculation, regardless of its fraction equivalent. It's particularly helpful when dealing with percentages that don't have simple fraction equivalents.
Method 3: Using Proportions
This method is based on setting up a proportion. We can represent the problem as:
x / 250 = 75 / 100
To solve for x (75% of 250), we can cross-multiply:
100x = 75 * 250
100x = 18750
x = 18750 / 100
x = 187.5
This method is a more formal approach, illustrating the underlying relationship between percentages and proportions. While slightly more complex, it reinforces the mathematical principles involved.
Method 4: Using a Calculator
Most calculators have a percentage function. Simply input "250 * 75%" (or the equivalent notation on your calculator) and the result, 187.5, will be displayed. This method is the quickest and most efficient for straightforward calculations.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of daily life:
- Shopping and Sales: Calculating discounts (e.g., a 20% discount on a $100 item), sales tax, and final prices after discounts and taxes.
- Finance: Determining interest rates, calculating loan payments, analyzing investment returns, and understanding financial statements.
- Statistics: Representing data as percentages, interpreting statistical results, and understanding probabilities.
- Science: Expressing concentrations, calculating experimental yields, and representing data in scientific reports.
- Everyday Life: Determining tips at restaurants, understanding tax rates, calculating proportions in recipes, and more.
Practical Examples
Let's explore some practical examples to solidify our understanding:
-
Scenario 1: Sales Discount: A store offers a 75% discount on a $250 item. Using the methods described above, we find that the discount amount is $187.50. The final price would be $250 - $187.50 = $62.50.
-
Scenario 2: Exam Scores: A student scored 75 out of 250 on an exam. To express this as a percentage, we divide the score by the total points and multiply by 100: (75/250) * 100 = 30%. The student achieved a score of 30%.
-
Scenario 3: Tax Calculation: Suppose a sales tax is 7.5% and the cost of an item is $250. To calculate the tax amount, we find 7.5% of 250: 0.075 * 250 = $18.75. The total cost, including tax, would be $250 + $18.75 = $268.75.
Advanced Percentage Calculations
While this article focuses on calculating a percentage of a single number, percentage calculations can become more complex. Here are some advanced concepts:
-
Percentage Increase/Decrease: Calculating the percentage change between two numbers. For example, if a quantity increases from 200 to 250, the percentage increase is calculated as [(250-200)/200] * 100 = 25%.
-
Percentage Points: It's crucial to understand the difference between percentage points and percentages. For instance, if interest rates increase from 5% to 10%, this is a 5 percentage point increase, not a 100% increase.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. It's a more complex calculation frequently used in financial contexts.
-
Percentage of a Percentage: Calculating a percentage of a percentage requires multiplying the two percentages together. For example, 10% of 25% is 0.10 * 0.25 = 0.025 or 2.5%.
Further Learning Resources
For those seeking to delve deeper into percentage calculations and related mathematical concepts, numerous online resources are available. Websites, educational platforms, and textbooks offer comprehensive explanations, practice problems, and interactive exercises. Consider searching for "percentage calculator," "percentage increase/decrease calculator," or "compound interest calculator" for online tools to aid your calculations.
Remember, practice is key to mastering any mathematical skill. By working through various examples and applying these techniques to real-world scenarios, you will build confidence and proficiency in calculating percentages. Understanding percentages is a fundamental skill applicable across many areas of life, so the time invested in learning them will prove invaluable.
Latest Posts
Latest Posts
-
4 420 Divided By 170
Sep 25, 2025
-
Another Word For Foreshadowing Is
Sep 25, 2025
-
20 Deg C To F
Sep 25, 2025
-
Particle Diagram Of Solid Sand
Sep 25, 2025
-
Which Describes Human Made Polymers
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.