What Is 75 Of 27
gasmanvison
Sep 12, 2025 · 5 min read
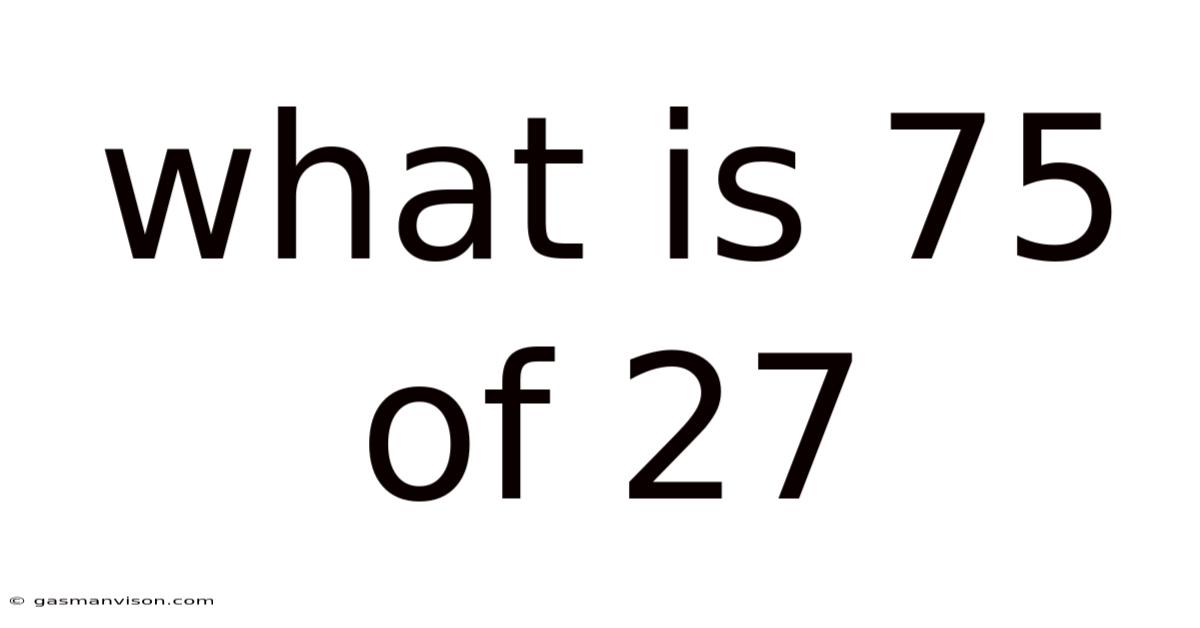
Table of Contents
What is 75% of 27? A Comprehensive Guide to Percentage Calculations
Finding 75% of 27 might seem like a simple task, but understanding the underlying principles of percentage calculations is crucial for a wide range of applications, from everyday budgeting and shopping to complex financial analysis and data interpretation. This article will not only answer the question directly but will also delve into the various methods for calculating percentages, exploring different approaches and highlighting their practical uses. We'll also look at how to apply these methods to similar problems and touch on the importance of understanding percentages in various contexts.
Understanding Percentages:
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred" – it represents a proportion out of a whole. For instance, 75% means 75 out of 100, which can also be expressed as the fraction 75/100 or the decimal 0.75. This fundamental understanding is key to tackling any percentage calculation.
Method 1: Using Decimal Conversion
This is arguably the most straightforward method for calculating percentages. It involves converting the percentage into its decimal equivalent and then multiplying it by the number.
-
Convert the percentage to a decimal: To convert 75% to a decimal, divide it by 100: 75 / 100 = 0.75
-
Multiply the decimal by the number: Now, multiply the decimal (0.75) by the number you want to find the percentage of (27): 0.75 * 27 = 20.25
Therefore, 75% of 27 is 20.25.
This method is efficient and readily adaptable to various percentage calculations. It's particularly useful when using calculators, as it minimizes the number of steps involved.
Method 2: Using Fraction Conversion
Percentages can also be expressed as fractions. This method provides a more intuitive understanding of the underlying mathematical operation.
-
Convert the percentage to a fraction: 75% can be written as the fraction 75/100. This fraction can be simplified by dividing both the numerator and denominator by their greatest common divisor (25): 75/100 = 3/4
-
Multiply the fraction by the number: Now, multiply the simplified fraction (3/4) by the number (27): (3/4) * 27 = 81/4
-
Convert the improper fraction to a decimal: To obtain the decimal value, divide the numerator (81) by the denominator (4): 81 / 4 = 20.25
Therefore, 75% of 27 is 20.25. This method demonstrates the equivalence between fractions, decimals, and percentages.
Method 3: Using Proportions
This method utilizes the concept of ratios and proportions to solve percentage problems. It's a more versatile approach, particularly useful when dealing with more complex percentage scenarios.
-
Set up a proportion: We can set up a proportion to represent the problem: x/27 = 75/100, where 'x' represents the unknown value (75% of 27).
-
Cross-multiply: Cross-multiply the proportion to solve for 'x': 100x = 75 * 27
-
Solve for x: 100x = 2025. Divide both sides by 100: x = 2025 / 100 = 20.25
Therefore, 75% of 27 is 20.25. This method showcases the relational aspect of percentages, emphasizing the proportional relationship between the parts and the whole.
Practical Applications of Percentage Calculations:
Understanding percentage calculations is essential in numerous real-world situations:
-
Financial Calculations: Calculating discounts, interest rates, taxes, tips, and profit margins all involve percentages. For example, calculating a 15% tip on a restaurant bill or determining the interest accrued on a savings account.
-
Data Analysis: Percentages are extensively used in data interpretation and representation. Analyzing survey results, market share, growth rates, and statistical data often requires calculating and understanding percentages. For instance, understanding the percentage change in sales from one year to the next or interpreting the percentage distribution of survey responses.
-
Everyday Life: Calculating sales tax, discounts on items, or determining the percentage of ingredients in a recipe all require an understanding of percentage calculations. For example, figuring out how much you will save on a sale item with a 20% discount or what percentage of your daily calorie intake comes from carbohydrates.
-
Academic and Scientific Fields: Percentages play a crucial role in various scientific and academic disciplines, including statistics, chemistry, physics, and biology. For instance, calculating the percentage yield of a chemical reaction or representing the percentage composition of an element in a compound.
Solving Similar Problems:
The methods outlined above can be easily adapted to solve similar percentage problems. For instance, to calculate 25% of 50, you would:
- Method 1 (Decimal Conversion): 0.25 * 50 = 12.5
- Method 2 (Fraction Conversion): (1/4) * 50 = 12.5
- Method 3 (Proportions): x/50 = 25/100, which solves to x = 12.5
Similarly, to find 60% of 120, you would use the same methods, substituting the appropriate values. The key is to understand the underlying principles and adapt the methodology accordingly.
Beyond Simple Percentage Calculations:
While this article focused on calculating a simple percentage, the principles extend to more complex scenarios:
-
Percentage Increase/Decrease: These calculations involve determining the percentage change between two values. For instance, finding the percentage increase in sales from one year to the next.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest from previous periods. Understanding compound interest is crucial for long-term financial planning.
-
Percentage Points: This is a crucial distinction often overlooked. Percentage points refer to the difference between two percentages, not the percentage difference. For example, a change from 20% to 25% is a 5-percentage-point increase, but a 25% increase of 20%.
Mastering percentage calculations empowers you to confidently approach a wide range of quantitative problems. The ability to convert between percentages, decimals, and fractions, combined with a solid understanding of proportional reasoning, is essential for success in many areas of life, both personal and professional. From everyday budgeting to complex financial models, the ability to calculate and interpret percentages is an invaluable skill.
Latest Posts
Latest Posts
-
21st Letter Of The Alphabet
Sep 12, 2025
-
Use Cacophonous In A Sentence
Sep 12, 2025
-
Referenceerror Textencoder Is Not Defined
Sep 12, 2025
-
What Is 200ml In Oz
Sep 12, 2025
-
Is Philosophy A Social Science
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Of 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.