What Is 80 Of 120
gasmanvison
Sep 21, 2025 · 5 min read
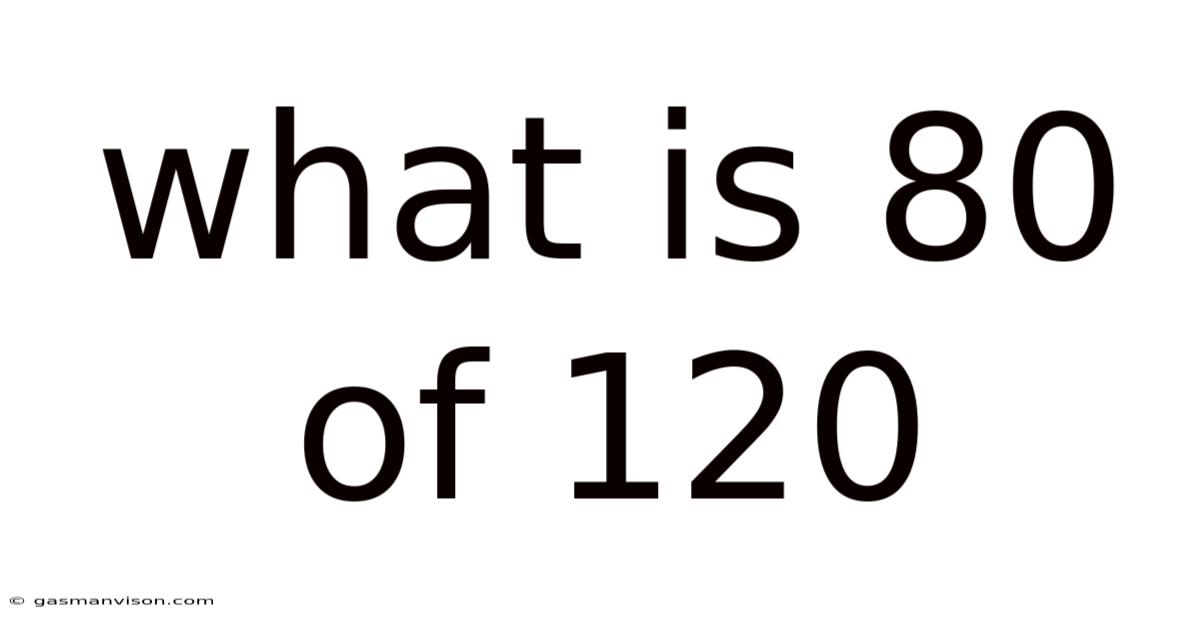
Table of Contents
What is 80% of 120? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 80% of 120?", opens the door to a broader understanding of percentages, their calculations, and their widespread applications in various fields. While the answer itself is easily obtainable through a simple calculation, exploring the underlying concepts and real-world examples provides a richer learning experience. This article will not only answer the question directly but also delve into the methodology, explore different approaches to solving percentage problems, and demonstrate the practical relevance of percentages in everyday life and professional contexts.
Meta Description: Learn how to calculate 80% of 120 and explore the world of percentages. This comprehensive guide explains different calculation methods, real-world applications, and offers practical tips for mastering percentage calculations.
Calculating 80% of 120: The Basic Approach
The most straightforward way to calculate 80% of 120 is to convert the percentage to a decimal and then multiply it by the number. 80% can be written as 0.80 (or simply 0.8). Therefore, the calculation is:
0.8 * 120 = 96
Therefore, 80% of 120 is 96.
Alternative Methods for Calculating Percentages
While the above method is efficient, understanding alternative methods can be beneficial, especially when dealing with more complex percentage problems or when working without a calculator.
Method 1: Using Fractions:
Percentages can be expressed as fractions. 80% is equivalent to 80/100, which simplifies to 4/5. Therefore, calculating 80% of 120 can be done as follows:
(4/5) * 120 = 4 * (120/5) = 4 * 24 = 96
This method is useful when dealing with percentages that have easily simplified fractional equivalents.
Method 2: Finding 10% and Scaling Up:
This method is particularly helpful for mental calculations. Finding 10% of a number is simply dividing it by 10. 10% of 120 is 12. Since 80% is eight times 10%, we multiply 12 by 8:
12 * 8 = 96
Method 3: Using Proportions:
This method is based on setting up a proportion. We can set up a proportion as follows:
80/100 = x/120
To solve for x (which represents 80% of 120), we cross-multiply:
100x = 80 * 120 100x = 9600 x = 9600/100 x = 96
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in a wide range of situations, both in personal life and professional settings. Here are some examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For instance, understanding the interest rate on a loan or the annual percentage yield (APY) on a savings account requires a firm grasp of percentages. Similarly, calculating the discount on a sale item or the tax amount on a purchase involves percentage calculations.
-
Sales and Marketing: Companies use percentages to track sales growth, conversion rates, market share, and customer acquisition costs. Marketing campaigns often involve setting targets and measuring performance based on percentage increases or decreases. For example, a marketing team might aim for a 15% increase in website traffic or a 10% conversion rate from leads to sales.
-
Data Analysis and Statistics: Percentages are frequently used to represent data in a clear and concise manner. Charts, graphs, and reports often utilize percentages to illustrate proportions, trends, and comparisons. For instance, data analysis may show that 70% of customers prefer a specific product feature or that 25% of website visitors make a purchase.
-
Education: Grades are often expressed as percentages, reflecting a student's performance on tests and assignments. Understanding percentages is essential for interpreting academic progress and setting academic goals. Furthermore, understanding statistical analysis, often expressed in percentages, helps in interpreting research findings and making informed decisions.
-
Everyday Life: From calculating tips in restaurants to understanding sale prices in stores, percentages are omnipresent in daily life. Understanding percentages helps us make informed decisions about budgeting, spending, and saving money.
Beyond the Basics: More Complex Percentage Problems
While calculating 80% of 120 is relatively straightforward, percentage problems can become more complex. Here are a few examples:
- Finding the original amount: If you know that 80% of a number is 96, how can you find the original number? This involves working backward using the percentage equation. Let's represent the original number as 'y':
0.8y = 96 y = 96 / 0.8 y = 120
- Percentage increase/decrease: Suppose a product's price increased from 100 to 120. What is the percentage increase? First, calculate the difference (120 - 100 = 20). Then, divide the difference by the original amount and multiply by 100:
(20 / 100) * 100 = 20%
- Percentage change with multiple increases/decreases: Imagine a price increases by 10% and then decreases by 10%. The final price isn't the same as the original price due to the compounding effect. These types of problems require a step-by-step approach, carefully calculating each percentage change sequentially.
Mastering Percentage Calculations: Tips and Tricks
Here are a few tips to improve your proficiency with percentage calculations:
-
Practice regularly: The key to mastering any mathematical concept is consistent practice. Work through various percentage problems to build your understanding and confidence.
-
Use different methods: Experiment with different methods of calculating percentages to find the approach that best suits your understanding and the specific problem.
-
Use a calculator strategically: While calculators can speed up calculations, it’s important to understand the underlying principles. Use calculators for complex calculations but practice mental calculations for simpler problems to improve your understanding.
-
Break down complex problems: Complex percentage problems can be simplified by breaking them down into smaller, more manageable steps.
-
Check your answers: Always check your answers using different methods or by working backward to ensure accuracy.
Conclusion
The question "What is 80% of 120?" serves as a springboard for exploring the broader topic of percentages and their significance. While the answer, 96, is readily obtained, the underlying concepts and their applications are far-reaching. Understanding percentages is crucial for navigating various aspects of personal finance, professional endeavors, and everyday life. By mastering percentage calculations and their diverse applications, you equip yourself with valuable skills for informed decision-making and effective problem-solving in a wide array of contexts. Continuous practice and exploration of different calculation methods will enhance your proficiency and deepen your understanding of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
What Does Bd Mean Gang
Sep 22, 2025
-
English Class Is Like Simile
Sep 22, 2025
-
Interior Angle For A Hexagon
Sep 22, 2025
-
Swelling Of Legs Icd 10
Sep 22, 2025
-
In A Nonpartisan Election
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 80 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.