What Is 80 Of 1200
gasmanvison
Sep 02, 2025 · 5 min read
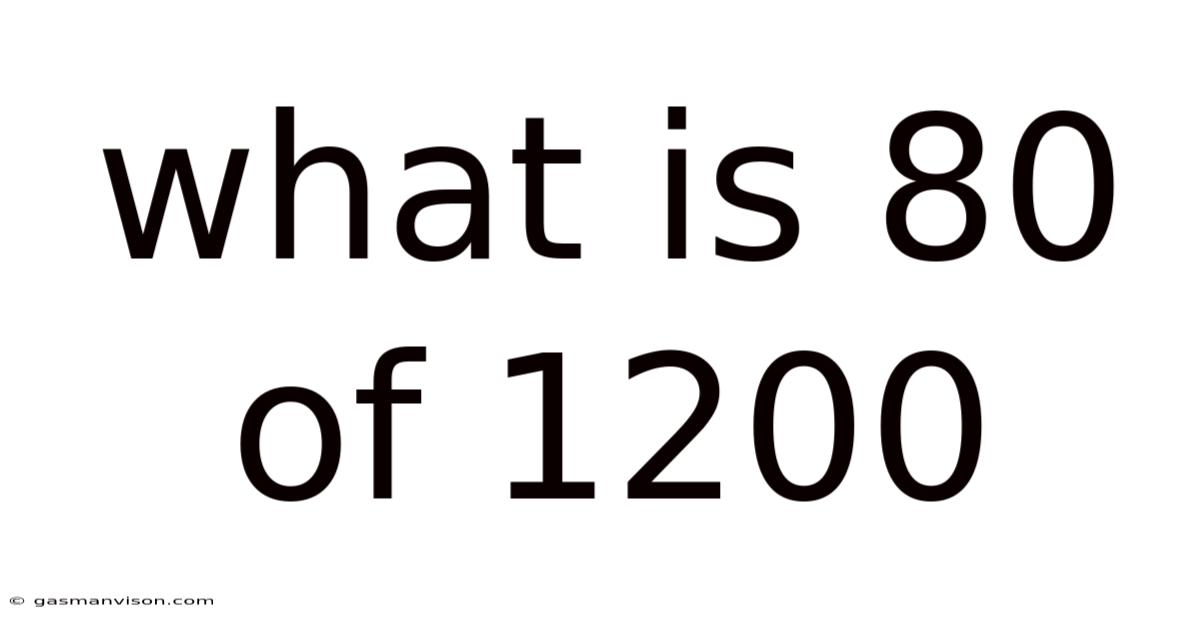
Table of Contents
What is 80% of 1200? A Deep Dive into Percentages and Their Applications
Finding 80% of 1200 is a simple percentage calculation, but understanding the underlying principles can unlock a world of practical applications in various fields. This article will not only answer the question directly but also explore the methods for calculating percentages, their importance in everyday life, and advanced applications in areas like finance, statistics, and more. The core concept is straightforward, but the implications are far-reaching.
Meta Description: Learn how to calculate 80% of 1200 and explore the broader applications of percentages in everyday life, finance, and more. This comprehensive guide covers various calculation methods and real-world examples.
First, let's answer the main question: 80% of 1200 is 960.
This can be calculated in a few different ways, each offering a slightly different perspective on the underlying mathematics:
Method 1: Converting Percentage to Decimal
This is the most common and arguably the simplest method. We convert the percentage (80%) into its decimal equivalent by dividing by 100:
80% = 80/100 = 0.8
Then, we multiply this decimal by the number we want to find the percentage of (1200):
0.8 * 1200 = 960
Therefore, 80% of 1200 is 960. This method is easily adaptable to any percentage calculation.
Method 2: Fraction Method
Percentages can also be expressed as fractions. 80% is equivalent to the fraction 80/100, which simplifies to 4/5. We then multiply this fraction by 1200:
(4/5) * 1200 = 4 * (1200/5) = 4 * 240 = 960
This method is particularly useful when dealing with percentages that easily translate into simple fractions.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the unknown value. We set up a proportion:
80/100 = x/1200
where 'x' represents the value we want to find (80% of 1200). To solve for x, we cross-multiply:
80 * 1200 = 100 * x
96000 = 100x
x = 96000/100 = 960
Practical Applications of Percentage Calculations
The ability to calculate percentages is crucial in many aspects of life. Here are a few examples:
-
Finance: Calculating interest on loans or savings accounts, determining discounts on purchases, understanding tax rates, analyzing investment returns, and comparing financial products all involve percentage calculations. For example, understanding the interest rate on a mortgage directly impacts monthly payments. Similarly, calculating the discount percentage on a sale item allows consumers to easily determine the final price.
-
Statistics: Percentages are fundamental in statistical analysis. They are used to represent data proportions, calculate probabilities, interpret survey results, and understand trends. For example, the success rate of a particular medical treatment might be expressed as a percentage. Similarly, consumer polls and market research often rely heavily on percentages to represent their findings.
-
Science: Percentages are used extensively in scientific research to express concentrations of solutions, error margins in experiments, and changes in quantities over time. For instance, the concentration of a chemical in a solution is often expressed as a percentage.
-
Everyday Life: Calculating tips in restaurants, determining the sale price of items, understanding nutritional information (e.g., percentage of daily value on food labels), and figuring out discounts on purchases all rely on percentage calculations. Even something as simple as splitting a bill equally among friends often involves calculating percentages.
-
Business: Businesses use percentages in myriad ways, from calculating profit margins and overhead costs to determining sales growth and market share. Profit margin, a key indicator of a company’s financial health, is directly related to percentage calculations.
Advanced Applications and Related Concepts
Beyond basic percentage calculations, there are more complex scenarios where a thorough understanding of percentages becomes invaluable:
-
Compound Interest: This involves calculating interest on the principal amount plus any accumulated interest. Understanding compound interest is critical for long-term financial planning, especially when dealing with investments and loans. The formula for compound interest incorporates percentage calculations to determine the final value of an investment after a specific period.
-
Percentage Change: This measures the relative change between two values. It's often used to track growth or decline in various areas, such as sales figures, population sizes, or stock prices. The formula for percentage change involves subtracting the initial value from the final value, dividing the result by the initial value, and then multiplying by 100%.
-
Percentage Point Difference: This is a crucial concept when comparing percentages. It represents the arithmetic difference between two percentages. For example, an increase from 10% to 15% is a 5 percentage point increase, not a 50% increase.
-
Weighted Averages: These are used when different data points have varying levels of importance or weight. Weighted averages often involve percentages to represent the contribution of each data point to the overall average.
-
Regression Analysis: In statistical modeling, regression analysis often uses percentage changes in variables to explore relationships between them. Understanding the percentage changes in independent variables allows researchers to understand their influence on dependent variables.
Beyond the Calculation: Developing Numerical Literacy
While calculating 80% of 1200 is a straightforward task, the broader implication of mastering percentage calculations is significant. It's a core component of numerical literacy—the ability to understand and apply mathematical concepts to real-world situations. This skill is increasingly essential in a world driven by data and quantitative analysis. Improving your numerical literacy not only enhances your problem-solving capabilities but also empowers you to make informed decisions in various aspects of your life. From managing your personal finances to interpreting data in your profession, a strong understanding of percentages is an invaluable asset.
In conclusion, while the answer to "What is 80% of 1200?" is 960, the significance of understanding percentages extends far beyond this single calculation. Mastering percentage calculations equips you with a fundamental tool for navigating the numerical landscape of modern life, empowering you to make informed decisions and effectively analyze data across various domains. The applications are diverse and essential for both personal and professional success.
Latest Posts
Latest Posts
-
Paper Based Pii Is Involved
Sep 02, 2025
-
18 Degrees C To F
Sep 02, 2025
-
Deduct For 3 4 Rigid 90
Sep 02, 2025
-
How Many Oz Is 350ml
Sep 02, 2025
-
Difference Between Shale And Slate
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 80 Of 1200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.