What Is 80 Of 24
gasmanvison
Sep 15, 2025 · 5 min read
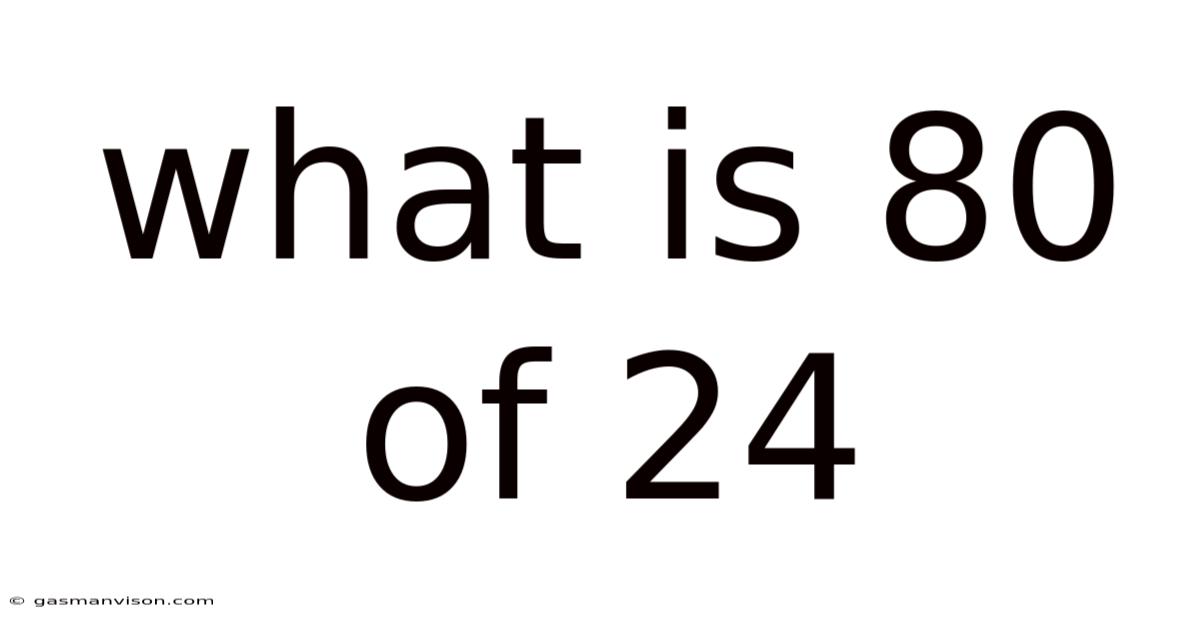
Table of Contents
What is 80% of 24? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 80% of 24?", opens the door to a fascinating exploration of percentages, their practical applications, and the underlying mathematical concepts. While the answer itself is easily calculated, understanding the process and its broader implications is crucial for numerous real-world scenarios, from financial calculations to scientific data analysis. This article will not only provide the solution but also delve into the methods for calculating percentages, explore different approaches, and illustrate their relevance across various fields.
Meta Description: Learn how to calculate 80% of 24 and understand the underlying mathematical concepts. This comprehensive guide explores percentage calculations, their real-world applications, and offers various methods for solving similar problems. Discover the power of percentages in everyday life and beyond.
Understanding Percentages: A Foundation
Percentages are a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). They provide a standardized method for comparing proportions and making relative comparisons across different datasets. Understanding percentages is fundamental to various areas, including:
- Finance: Calculating interest rates, discounts, profit margins, taxes, and investment returns.
- Science: Representing experimental results, statistical data, and error margins.
- Business: Analyzing market share, sales figures, and customer demographics.
- Everyday Life: Understanding discounts at stores, calculating tips, and interpreting statistics in news reports.
Calculating 80% of 24: Three Different Approaches
There are several ways to calculate 80% of 24. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
The most straightforward method involves converting the percentage to its decimal equivalent. To do this, divide the percentage by 100. In this case:
80% / 100 = 0.8
Now, multiply this decimal by the number you want to find the percentage of:
0.8 * 24 = 19.2
Therefore, 80% of 24 is 19.2.
Method 2: Using Fractions
Percentages can also be expressed as fractions. 80% can be written as 80/100, which simplifies to 4/5. To find 80% of 24, we multiply 24 by the fraction:
(4/5) * 24 = 96/5 = 19.2
This again gives us the answer: 19.2.
Method 3: Using Proportions
This method uses the concept of ratios and proportions. We can set up a proportion:
80/100 = x/24
where 'x' represents the value we want to find. To solve for 'x', we cross-multiply:
100x = 80 * 24 100x = 1920 x = 1920 / 100 x = 19.2
Once again, the result is 19.2.
Beyond the Calculation: Practical Applications and Extensions
The ability to calculate percentages extends far beyond this single example. Let's explore some real-world scenarios where understanding percentages is essential:
1. Sales and Discounts: Imagine a store offering an 80% discount on an item originally priced at $24. Using the methods outlined above, we know the discount would be $19.20, and the final price would be $24 - $19.20 = $4.80.
2. Financial Investments: If you invest $24 and your investment grows by 80%, your profit would be $19.20, resulting in a total of $43.20. Conversely, if your investment declined by 80%, you would lose $19.20, leaving you with $4.80.
3. Tax Calculations: If a 24% tax is levied on an item costing $100, the tax amount would be 24% of $100, which is $24. This is easily calculated using the decimal method (0.24 * 100 = 24).
4. Statistical Analysis: In data analysis, percentages are used to represent proportions and trends. For example, if 80% of survey respondents prefer a particular product, this indicates strong market preference.
5. Scientific Measurements: In scientific research, percentages are often used to express error margins or variations in experimental results. For example, a measurement might be reported as 24 units ± 80%, indicating a significant degree of uncertainty.
Advanced Percentage Calculations and Problem-Solving
The fundamental principles of percentage calculation can be extended to solve more complex problems:
-
Finding the percentage one number represents of another: For instance, what percentage is 19.2 of 24? This can be calculated as (19.2 / 24) * 100 = 80%.
-
Calculating percentage increase or decrease: This involves comparing two numbers and expressing the change as a percentage. For example, if a quantity increases from 20 to 24, the percentage increase is [(24 - 20) / 20] * 100 = 20%.
-
Working with compound percentages: This involves calculating percentages of percentages, often seen in compound interest calculations or population growth models.
Mastering Percentages: Tips and Tricks
Here are some tips for mastering percentage calculations and problem-solving:
- Practice regularly: Consistent practice is key to developing proficiency.
- Use different methods: Try each of the methods described above to find the one that best suits your understanding.
- Visualize the problem: Draw diagrams or use real-world examples to visualize the problem.
- Break down complex problems: Decompose complex problems into smaller, manageable steps.
- Utilize online calculators and tools: Various online calculators can help you check your work and build confidence.
Conclusion: The Ubiquity of Percentages
This in-depth exploration of the seemingly simple question, "What is 80% of 24?", has revealed the wide-ranging applications of percentage calculations. From everyday financial transactions to complex scientific analyses, understanding percentages is a valuable skill applicable across numerous disciplines. By mastering the fundamental concepts and practicing various calculation methods, you can confidently tackle percentage-related problems and utilize this powerful tool to interpret data and make informed decisions. The ability to calculate percentages effectively is a crucial component of numeracy and essential for navigating the complexities of the modern world.
Latest Posts
Latest Posts
-
Every Quadrilateral Is A Rhombus
Sep 15, 2025
-
Do Male Cows Have Udders
Sep 15, 2025
-
Why Walmart Failed In Germany
Sep 15, 2025
-
What Is 35 Of 40
Sep 15, 2025
-
11 2 Cups In Oz
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 80 Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.