What Is Half Of 4+4
gasmanvison
Sep 22, 2025 · 5 min read
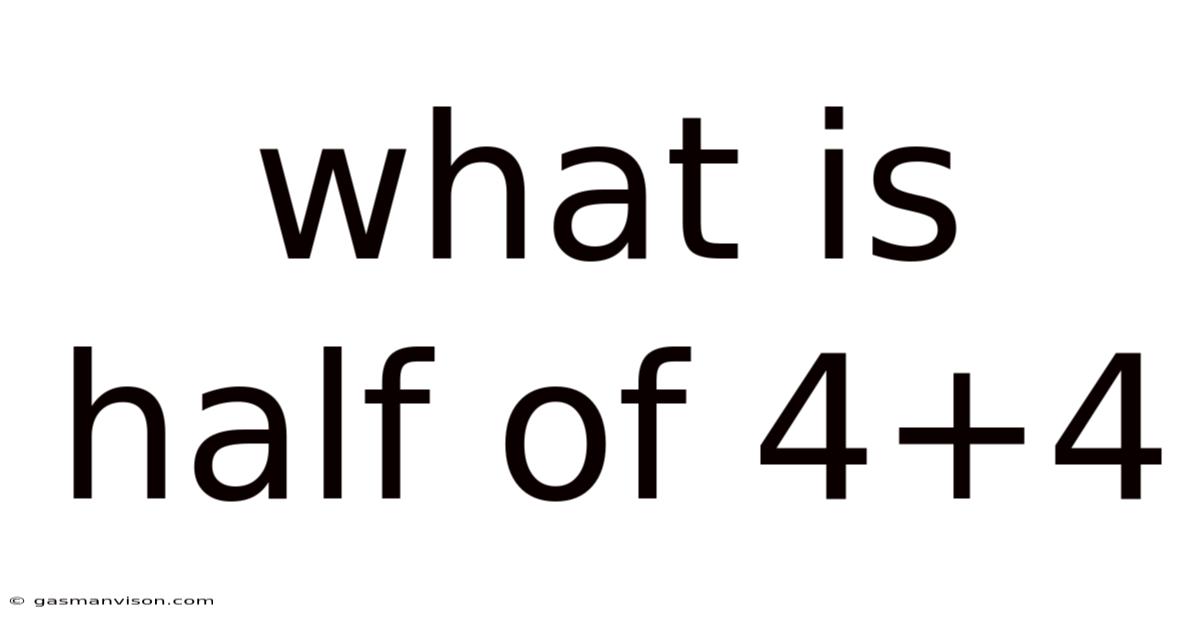
Table of Contents
What is Half of 4 + 4? A Deep Dive into Simple Arithmetic and its Broader Implications
This seemingly simple question, "What is half of 4 + 4?", opens a door to a surprisingly expansive exploration of fundamental arithmetic, order of operations, and even the philosophical implications of mathematical certainty. While the answer itself is straightforward, the process of arriving at it, and the understanding we gain along the way, is far more enriching. This article will not only answer the question but also delve into related mathematical concepts, practical applications, and the broader significance of seemingly basic arithmetic problems.
Meta Description: Uncover the surprisingly deep answer to "What is half of 4 + 4?". This article explores basic arithmetic, order of operations (PEMDAS/BODMAS), real-world applications, and the fascinating implications of even the simplest mathematical problems.
Understanding the Order of Operations: PEMDAS/BODMAS
Before we solve the problem, it's crucial to understand the order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). These acronyms represent the sequence in which mathematical operations should be performed to ensure a consistent and accurate result. In our equation, "half of 4 + 4," we encounter addition and multiplication (implied by "half of").
Following PEMDAS/BODMAS, we prioritize multiplication (finding half) before addition.
Step-by-Step Solution
-
Multiplication (Finding Half): "Half of 4" means 4 divided by 2, which equals 2.
-
Addition: Now we have 2 + 4. Adding these together gives us 6.
Therefore, the answer to "What is half of 4 + 4?" is 6.
Beyond the Basics: Exploring Related Concepts
While the solution is simple, let's explore some related mathematical concepts that build upon this foundational understanding:
1. Fractions and Decimals: Alternative Representations
The phrase "half of" implies a fraction (1/2). We can rewrite the problem using fractions: (1/2) * 4 + 4. This illustrates the interchangeability between fractions and decimals in mathematical expressions. We can also express "half" as 0.5, resulting in the equation 0.5 * 4 + 4. Understanding these alternative representations enhances our mathematical flexibility.
2. Distributive Property: An Alternative Approach
The distributive property of multiplication over addition allows us to solve the problem in a slightly different way. We can rewrite the expression as: (1/2) * (4 + 4). This simplifies to (1/2) * 8, which again equals 4. This demonstrates that different approaches can lead to the same correct answer, highlighting the elegance and consistency of mathematics.
3. Algebraic Representation: Generalizing the Problem
We can generalize this problem using algebra. Let's replace 4 with the variable 'x'. Our problem then becomes "What is half of x + x?". This can be written as (1/2)x + x. Simplifying this algebraic expression, we get (3/2)x or 1.5x. This shows how a simple arithmetic problem can be generalized to represent a broader mathematical concept. If we substitute x = 4, we get (3/2)*4 = 6, confirming our original solution.
4. Real-World Applications: Everyday Uses of Basic Arithmetic
This seemingly simple arithmetic problem has numerous real-world applications. Consider these scenarios:
- Dividing resources: If you have 8 cookies and want to share half with a friend, this problem directly applies.
- Calculating discounts: A 50% discount on a $8 item can be calculated using this same principle.
- Portioning ingredients: Baking recipes often require halving or doubling ingredients, necessitating a similar calculation.
- Understanding percentages: "Half of" is equivalent to 50%, a commonly used percentage in various contexts, from sales discounts to statistical analysis.
These examples highlight how basic arithmetic is integral to numerous everyday tasks, emphasizing the practical importance of mastering fundamental mathematical skills.
The Philosophical Implications of Mathematical Certainty
Beyond its practical applications, this simple arithmetic problem touches upon the philosophical aspect of mathematical certainty. The solution, 6, is an undeniable truth. This unwavering certainty contrasts with many aspects of life characterized by uncertainty and ambiguity. Mathematics provides a realm of absolute truths, offering a sense of order and predictability in a world often characterized by chaos. The consistent application of rules and the guaranteed arrival at a correct answer provide a foundation for trust and reliability in the field of mathematics.
Expanding Our Understanding: Further Exploration
To further solidify our understanding, let's explore variations of the original problem:
- What is half of 6 + 6? Following the same process, we get (1/2) * 6 + 6 = 3 + 6 = 9.
- What is half of 10 + 10? This yields (1/2) * 10 + 10 = 5 + 10 = 15.
- What is one-third of 6 + 6? This changes the fraction, requiring us to perform (1/3) * 6 + 6 = 2 + 6 = 8.
These variations demonstrate the adaptability of the solution process to different numbers and fractions. Each problem reinforces the importance of adhering to the order of operations and understanding the underlying principles of arithmetic.
Conclusion: The Power of Simple Arithmetic
The seemingly trivial question, "What is half of 4 + 4?", unfolds into a rich exploration of fundamental mathematical concepts, practical applications, and even philosophical implications. While the answer is a simple 6, the journey to arrive at that answer reveals the beauty and power of basic arithmetic. Mastering such fundamental principles provides a strong foundation for more advanced mathematical explorations and a deeper understanding of the world around us. The consistent application of rules, the unwavering certainty of results, and the broad applicability to everyday scenarios underscore the enduring significance of simple arithmetic. It's a testament to the power of seemingly basic calculations to illuminate complex ideas and solve real-world problems. The next time you encounter a simple mathematical problem, remember that the process of solving it can be just as valuable as the answer itself.
Latest Posts
Latest Posts
-
When Making Computer Assisted Dives
Sep 22, 2025
-
Langston Hughes Most Famous Poem
Sep 22, 2025
-
Influences Such As Childhood Experiences
Sep 22, 2025
-
What Is 375 In Inches
Sep 22, 2025
-
11 8 In Decimal Form
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 4+4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.