What Times 3 Equals 48
gasmanvison
Sep 02, 2025 · 5 min read
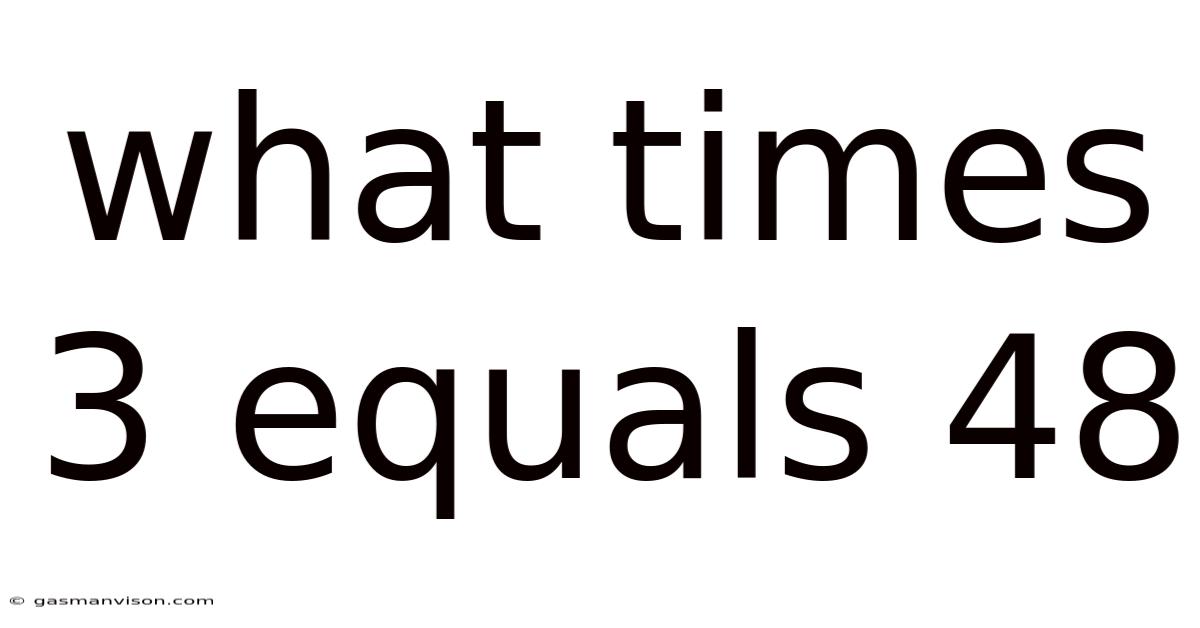
Table of Contents
What Times 3 Equals 48? A Deep Dive into Multiplication and Problem Solving
This seemingly simple question, "What times 3 equals 48?", opens the door to a broader exploration of multiplication, problem-solving strategies, and even the underlying mathematical principles at play. While the immediate answer is straightforward, understanding the why behind the answer offers valuable insights into mathematical thinking and its applications. This article will not only provide the solution but also delve into various approaches to solve this problem and explore related concepts.
Meta Description: Discover the answer to "What times 3 equals 48?" and explore different methods to solve this multiplication problem. We'll delve into the underlying mathematical concepts and explore related problem-solving strategies.
1. The Direct Approach: Finding the Missing Factor
The most direct way to solve "What times 3 equals 48?" is to recognize it as a simple multiplication problem where one factor is unknown. We can represent this algebraically as:
3 * x = 48
To find the value of 'x', we need to isolate it. This is done by dividing both sides of the equation by 3:
x = 48 / 3
Performing the division gives us:
x = 16
Therefore, 16 times 3 equals 48. This is the fundamental and quickest way to arrive at the solution.
2. Exploring Different Problem-Solving Strategies
While the direct approach is efficient, exploring alternative strategies enhances our understanding of mathematical concepts and problem-solving skills. Let's explore some different approaches:
-
Repeated Addition: Multiplication can be visualized as repeated addition. This means 3 * 16 is the same as adding 3 sixteen times: 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 48. This method, although more time-consuming for larger numbers, reinforces the foundational relationship between addition and multiplication.
-
Division as the Inverse of Multiplication: We already utilized this in the direct approach. Understanding that division is the inverse operation of multiplication is crucial. If we know the product (48) and one factor (3), we can use division to find the missing factor. This emphasizes the interconnectedness of arithmetic operations.
-
Using a Multiplication Table: A multiplication table provides a readily available resource to solve this problem. By looking at the row for 3, you can quickly find that 3 multiplied by 16 equals 48. This method is particularly useful for smaller numbers and reinforces memorization of multiplication facts.
-
Estimation and Mental Math: Before performing the calculation, estimation can be a valuable tool. Knowing that 3 * 10 = 30 and 3 * 20 = 60, we can quickly estimate that the answer lies between 10 and 20. This approach helps develop number sense and mental math skills.
3. Extending the Concept: Applications and Real-World Examples
Understanding "What times 3 equals 48?" extends beyond a simple arithmetic problem. It has practical applications in various real-world scenarios:
-
Dividing Objects: Imagine you have 48 candies and want to divide them equally among 3 friends. The solution (16) tells you each friend will receive 16 candies. This illustrates the practical application of division in everyday situations.
-
Calculating Costs: If 3 identical items cost 48 dollars, each item costs 16 dollars (48/3 = 16). This demonstrates the use of division in calculating unit costs.
-
Measurement and Conversion: Imagine you have a 48-meter-long rope and you want to cut it into 3 equal parts. Each part will be 16 meters long. This showcases the application in measurement and conversion problems.
-
Proportions and Ratios: This problem can be framed as a proportion: 3:48 :: 1:x. Solving for x gives the same result, 16. This introduces the concept of proportions and ratios, which are fundamental in various fields like chemistry, physics, and engineering.
4. Delving Deeper: Mathematical Properties and Concepts
This seemingly basic problem touches upon several important mathematical properties and concepts:
-
Commutative Property of Multiplication: Multiplication is commutative, meaning the order of the factors does not affect the product. 3 * 16 is the same as 16 * 3. This property simplifies calculations and provides flexibility in problem-solving.
-
Associative Property of Multiplication: When multiplying more than two numbers, the grouping of the factors does not change the product. This property is particularly useful when dealing with more complex calculations.
-
Distributive Property of Multiplication over Addition: This property allows us to break down complex multiplication problems into simpler ones. For example, 3 * (10 + 6) = (3 * 10) + (3 * 6) = 30 + 18 = 48. This property is crucial for simplifying algebraic expressions and solving equations.
-
Identity Property of Multiplication: Any number multiplied by 1 remains the same. This property might seem trivial, but it is fundamental to understanding the structure of the number system.
5. Problem-Solving Approaches for More Complex Scenarios
While this specific problem is easily solved, let's consider how the underlying principles apply to more complex scenarios:
-
Multi-step Problems: Imagine a scenario where you need to buy 3 packs of pencils, each costing 12 dollars, and then calculate the total cost including a 4 dollar tax. This involves multiple steps: multiplying the number of packs by the cost per pack, then adding the tax. The ability to break down a complex problem into smaller, manageable steps is crucial for successful problem-solving.
-
Word Problems: Word problems often require translating the problem's description into mathematical expressions. Understanding the context and identifying the relevant information is essential for setting up the correct equation. For example, a problem might say, "John has 3 times as many apples as Mary, and John has 48 apples. How many apples does Mary have?" This requires recognizing that the problem involves division to find the solution (48/3 = 16).
-
Algebraic Equations: As we saw earlier, this problem can be easily represented as an algebraic equation (3 * x = 48). Solving algebraic equations is a fundamental skill in mathematics and has applications in various fields like science, engineering, and finance.
6. Conclusion: The Importance of Foundational Math Skills
The seemingly simple question, "What times 3 equals 48?", reveals a wealth of mathematical concepts and problem-solving strategies. Mastering these foundational skills is essential for success in more advanced mathematical concepts and their applications in various aspects of life. By exploring different approaches and understanding the underlying principles, we not only find the answer but also cultivate a deeper appreciation for the beauty and power of mathematics. The ability to think critically, break down problems, and utilize different strategies are valuable skills that extend far beyond the realm of mathematics. The solution, 16, is merely the beginning of a much richer understanding of mathematical thinking.
Latest Posts
Latest Posts
-
How Are These Excerpts Similar
Sep 03, 2025
-
Conversion From Mg To Ml
Sep 03, 2025
-
Whats The Capital Of Kansas
Sep 03, 2025
-
How Many Feet Is 67
Sep 03, 2025
-
How Many Feet Is 72
Sep 03, 2025
Related Post
Thank you for visiting our website which covers about What Times 3 Equals 48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.