What Times What Equal 54
gasmanvison
Sep 06, 2025 · 6 min read
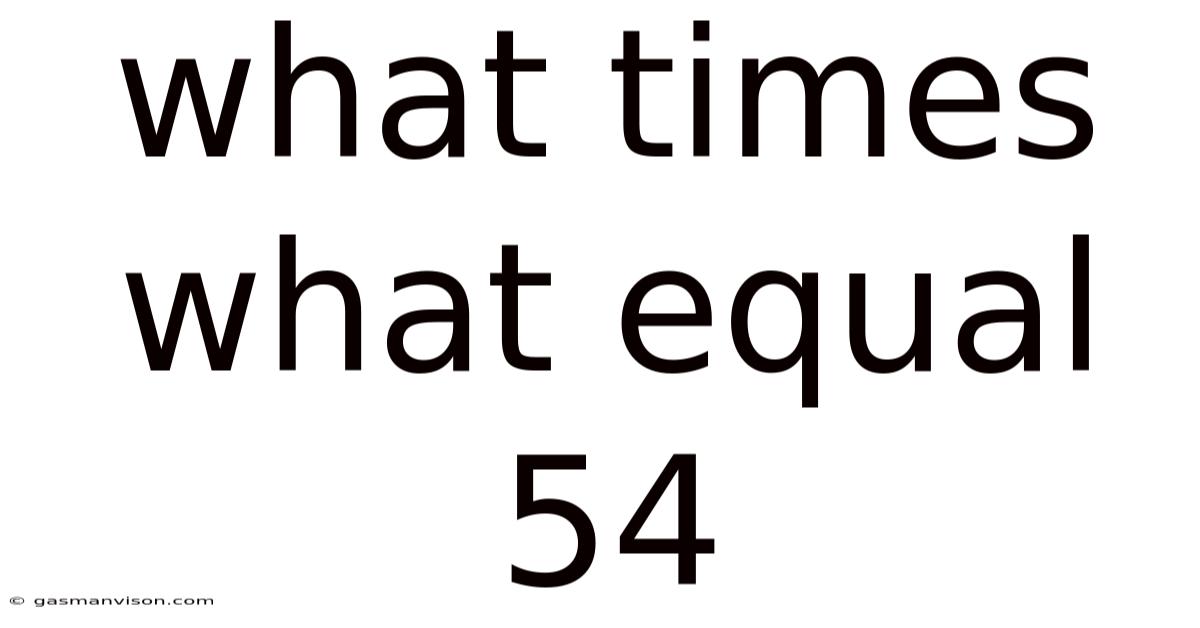
Table of Contents
What Times What Equals 54? Exploring the Factors and Applications of Multiplication
This seemingly simple question, "What times what equals 54?", opens the door to a fascinating exploration of multiplication, factor pairs, and the diverse ways we use this fundamental mathematical concept in everyday life. This article delves into finding all the factor pairs of 54, discusses the importance of understanding factors, and provides real-world examples showcasing the relevance of this seemingly basic mathematical operation. Understanding factors is crucial for various mathematical operations, from simplifying fractions to solving algebraic equations. Let's dive in!
Understanding Factors and Factor Pairs
Before we tackle the specific problem of finding numbers that multiply to 54, let's establish a solid understanding of factors and factor pairs. A factor is a whole number that divides evenly into another number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. A factor pair is a set of two factors that, when multiplied together, produce a specific number. For 12, the factor pairs are (1, 12), (2, 6), and (3, 4).
Finding all the factor pairs for a given number is a fundamental skill in arithmetic, and it’s essential for simplifying fractions, solving equations, and understanding more advanced mathematical concepts. It's also a crucial step in prime factorization, which is the process of breaking down a number into its prime factors (factors that are only divisible by 1 and themselves).
Finding the Factor Pairs of 54
Now, let's apply this knowledge to our question: "What times what equals 54?" We're looking for all the factor pairs of 54. We can systematically find them by starting with 1 and checking each whole number to see if it divides evenly into 54:
- 1 x 54: This is the first and most obvious factor pair.
- 2 x 27: 54 is an even number, so it's divisible by 2.
- 3 x 18: 54 is divisible by 3 (the sum of its digits, 5 + 4 = 9, is divisible by 3).
- 6 x 9: Since 2 and 3 are factors, their product, 6, is also a factor.
We've now found all the factor pairs of 54: (1, 54), (2, 27), (3, 18), and (6, 9). Notice that we can stop searching once we reach the square root of 54 (approximately 7.35). Any factor pairs beyond this point will simply be the reverse of pairs we've already found. For instance, if we continued, we’d find 9 x 6, which is the same as 6 x 9.
Beyond Simple Factor Pairs: Exploring Prime Factorization
Finding the factor pairs of 54 is a good starting point, but we can go further by exploring its prime factorization. Prime factorization is the process of expressing a number as a product of only prime numbers (numbers greater than 1 that are only divisible by 1 and themselves). The prime factors of 54 are 2 and 3. We can express this as 2 x 3 x 3 x 3, or 2 x 3³. Understanding prime factorization is essential in various mathematical applications, including simplifying fractions, finding the least common multiple (LCM), and greatest common divisor (GCD) of numbers.
Real-World Applications of Finding Factors
While finding the factors of 54 might seem like an abstract exercise, understanding factors has numerous practical applications in everyday life:
-
Dividing resources: Imagine you have 54 candies to distribute evenly among a group of friends. Knowing the factors of 54 allows you to determine how many friends you can give candies to without any leftovers. You could have 2 groups of 27, 3 groups of 18, 6 groups of 9, and so on.
-
Arranging objects: Suppose you're arranging 54 tiles to form a rectangular pattern. The factor pairs of 54 directly correspond to the possible dimensions of your rectangle. You could have a rectangle that is 1 tile wide and 54 tiles long, 2 tiles wide and 27 tiles long, and so on.
-
Baking and cooking: Many recipes involve dividing ingredients or adjusting quantities based on the number of servings. Understanding factors allows you to easily scale recipes up or down while maintaining the correct proportions. For instance, a recipe calling for 54 grams of flour could be adjusted to different quantities based on the factors of 54.
-
Geometry and area: Calculating the area of a rectangle involves multiplying its length and width. If you know the area (54 square units, for example), understanding factors helps you determine possible dimensions for the rectangle.
-
Algebra and equation solving: Factorization is a key technique used in solving quadratic equations and other algebraic expressions. Finding the factors of a number is an integral part of this process.
Expanding the Concept: Finding Numbers that Multiply to 54 with Variations
The question "What times what equals 54?" can be extended and made more complex. Consider these variations:
-
Using negative numbers: (-2) x (-27) = 54; (-3) x (-18) = 54; (-6) x (-9) = 54. This introduces the concept of multiplying negative numbers, where two negative numbers multiplied together result in a positive number.
-
Using fractions and decimals: 2.7 x 20 = 54; 1.5 x 36 = 54; 1/3 x 162 = 54. This showcases the versatility of multiplication and expands the scope beyond whole numbers.
-
Solving equations: The question could be embedded in a more complex equation, such as "x * y = 54, and x + y = 29." This requires solving a system of equations to find the values of x and y.
-
Working with variables: Introduce variables into the problem. For example: "If a * b = 54 and a = 6, what is the value of b?" This helps students understand algebraic concepts and apply the principle of finding factors.
Conclusion: The Enduring Importance of Understanding Multiplication and Factors
The seemingly simple question, "What times what equals 54?" serves as a gateway to a broader understanding of multiplication, factors, and their far-reaching applications. From simple tasks like dividing candies to more complex mathematical problems, the ability to find factor pairs and understand prime factorization is a crucial skill. This article has explored various aspects of this seemingly basic concept, showcasing its significance in various areas of mathematics and everyday life. By understanding factors and factor pairs, we equip ourselves with a fundamental mathematical tool that allows us to tackle more complex problems and better understand the world around us. The ability to recognize and work with factors is not just a mathematical skill, but a valuable tool applicable to many aspects of life.
Latest Posts
Latest Posts
-
How Many Pounds In 120kg
Sep 06, 2025
-
Iron Iii Sulfide Chemical Formula
Sep 06, 2025
-
Joseph Addison Quotes Weak Minds
Sep 06, 2025
-
3 5 Kg How Many Pounds
Sep 06, 2025
-
Birds Migrating Cats Chasing Prey
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equal 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.