What Times What Equals 17
gasmanvison
Sep 06, 2025 · 5 min read
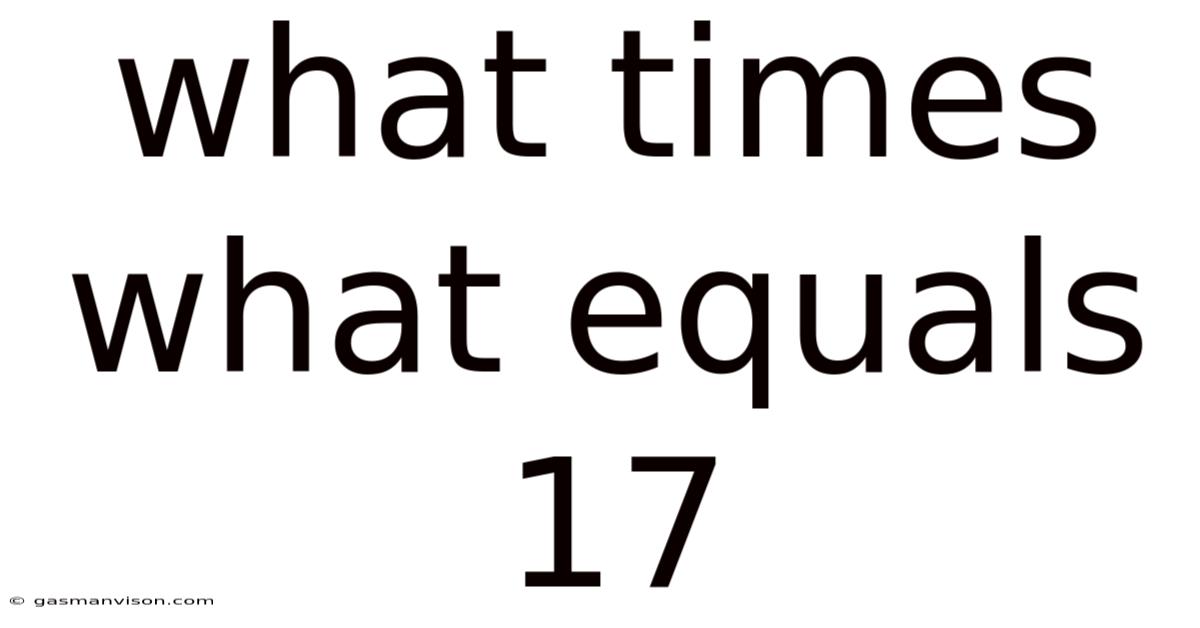
Table of Contents
What Times What Equals 17? Exploring Factor Pairs and Prime Numbers
Finding the answer to "What times what equals 17?" might seem deceptively simple at first glance. However, exploring this seemingly basic question opens up a fascinating world of number theory, delving into concepts like prime numbers, factors, and the unique properties of integers. This article will not only provide the answer but also explore the mathematical context surrounding it, enriching your understanding of fundamental arithmetic concepts. This exploration will touch upon the significance of prime numbers, their role in factorization, and how these concepts extend to more complex mathematical problems.
The Simple Answer and Its Implications
The answer is straightforward: 1 x 17 = 17. There are no other whole number factors that, when multiplied, result in 17. This seemingly simple solution unveils a crucial characteristic of the number 17: it's a prime number.
A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. This defining characteristic distinguishes prime numbers from composite numbers, which have more than two divisors. The fact that 17 only has 1 and 17 as factors directly answers our initial question and underscores its prime nature.
Understanding Prime Numbers: The Building Blocks of Arithmetic
Prime numbers are considered the fundamental building blocks of all whole numbers. This stems from the Fundamental Theorem of Arithmetic, which states that every whole number greater than 1 can be uniquely expressed as a product of prime numbers, regardless of the order of the factors. This theorem underpins many branches of mathematics, including cryptography and computer science.
For example, consider the number 12. Its prime factorization is 2 x 2 x 3 (or 2² x 3). No matter how you try to factorize 12 using different combinations of whole numbers, you will always end up with these same prime factors. This unique prime factorization is a cornerstone of number theory.
Exploring Factor Pairs and Their Significance
Factor pairs are sets of two numbers that, when multiplied, yield a specific product. In the case of 17, the only factor pair is (1, 17). Understanding factor pairs is crucial for simplifying fractions, solving equations, and understanding the divisibility rules of numbers. For larger numbers, finding all factor pairs can become more complex, often requiring systematic approaches and prime factorization.
For instance, let's consider the number 24. Its factor pairs include (1, 24), (2, 12), (3, 8), (4, 6). Each of these pairs, when multiplied, results in 24. Finding all factor pairs can be helpful in various mathematical contexts, such as determining the greatest common divisor (GCD) or least common multiple (LCM) of two numbers.
The Uniqueness of 17: A Prime Number's Properties
The fact that 17 is a prime number is significant for several reasons:
-
Divisibility: 17 is only divisible by 1 and itself. This property simplifies calculations involving divisibility tests and simplifies problems related to finding common factors or multiples.
-
Mathematical Applications: Prime numbers play a crucial role in cryptography, the science of secure communication. Algorithms used in encryption and decryption often rely on the difficulty of factoring large numbers into their prime components.
-
Number Theory: Prime numbers are a central subject of study in number theory, a branch of mathematics exploring the properties of integers. Many unsolved problems in mathematics relate directly to the behavior and distribution of prime numbers.
-
Infinite Nature: There are infinitely many prime numbers. This was proven by Euclid over 2000 years ago, demonstrating the endless richness and complexity of prime numbers.
Expanding the Question: What if we allowed for decimals or negative numbers?
The original question focused on whole numbers. If we expand the possibilities to include decimal numbers, then infinitely many pairs of numbers could multiply to 17. For example, 0.5 x 34 = 17, or 2 x 8.5 = 17. The same applies if we allow negative numbers: (-1) x (-17) = 17, (-0.5) x (-34) = 17, and so on. This highlights how the initial constraints of the question significantly influence the range of possible solutions.
Advanced Concepts Related to Prime Factorization
Understanding the prime factorization of a number allows for more advanced mathematical operations:
-
Greatest Common Divisor (GCD): The GCD of two numbers is the largest number that divides both without leaving a remainder. Prime factorization makes finding the GCD simpler.
-
Least Common Multiple (LCM): The LCM of two numbers is the smallest number that is a multiple of both. Prime factorization simplifies finding the LCM.
-
Modular Arithmetic: Modular arithmetic involves performing arithmetic operations within a specific range (modulo). Prime numbers play a crucial role in modular arithmetic, especially in cryptography.
Practical Applications of Prime Numbers and Factorization
Beyond theoretical mathematics, prime numbers and their factorization have tangible real-world applications:
-
Cryptography: As mentioned earlier, prime numbers are fundamental to modern encryption techniques, securing online transactions, communications, and sensitive data. The difficulty of factoring large numbers into their prime components forms the basis of many encryption algorithms.
-
Computer Science: Algorithms involving prime numbers are used in various computer science applications, including hash tables, random number generators, and error-correcting codes.
-
Coding Theory: Prime numbers find application in error detection and correction in data transmission and storage.
Conclusion: Beyond the Simple Answer
The seemingly simple question, "What times what equals 17?", leads to a deeper understanding of fundamental mathematical concepts. The answer, 1 x 17, reveals the prime nature of 17 and opens doors to a vast world of number theory, prime factorization, and its applications in various fields. Exploring this seemingly basic question not only solidifies your understanding of arithmetic but also highlights the elegance and power of mathematics in solving complex problems. The unique properties of prime numbers, including 17, demonstrate their significance as building blocks of numbers and their profound impact on various aspects of our technologically advanced world. From the simple act of multiplication to securing online transactions, the number 17 and its prime nature exemplify the interconnectedness of seemingly simple mathematical concepts with the complexities of modern technology.
Latest Posts
Latest Posts
-
7 5 4 Simulating A Coin Flip
Sep 06, 2025
-
21 Degrees Celcius To Farenheit
Sep 06, 2025
-
Convert 45 To A Decimal
Sep 06, 2025
-
Which Describes How Radiation Moves
Sep 06, 2025
-
240 Ml To Fl Oz
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 17 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.