What Times What Equals 52
gasmanvison
Sep 16, 2025 · 5 min read
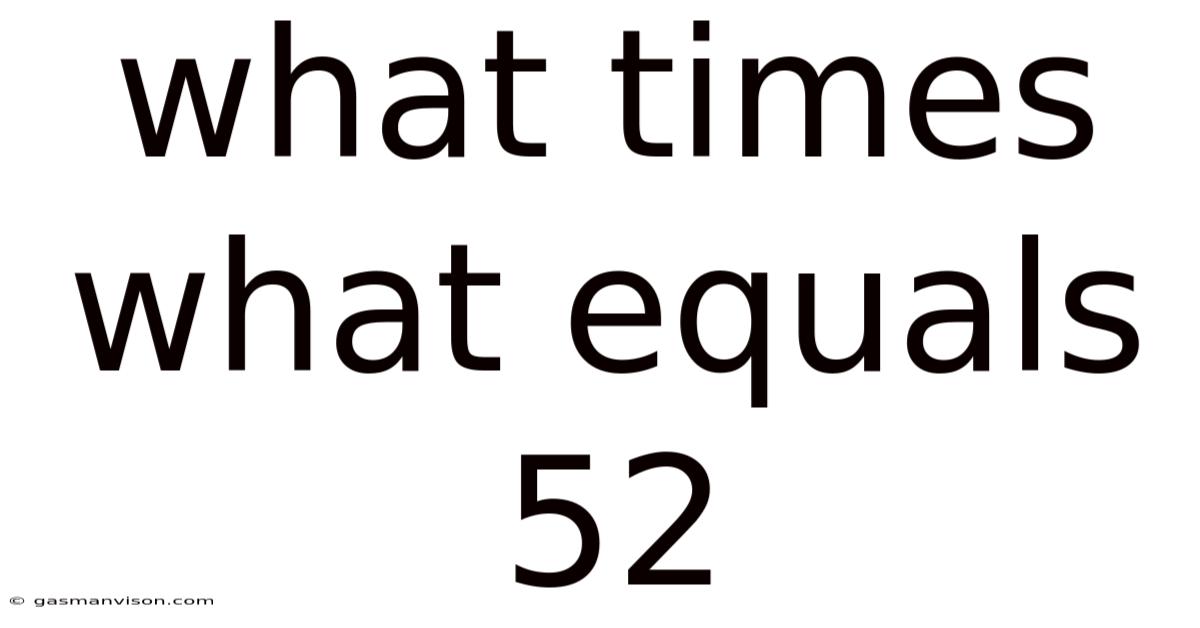
Table of Contents
What Times What Equals 52? Exploring the Factors and Applications of 52
Finding the numbers that multiply to equal 52 might seem like a simple arithmetic problem, but it opens the door to exploring fundamental concepts in mathematics, from basic factorization to more advanced applications in algebra and beyond. This article dives deep into the different ways to approach this question, examining the factors of 52, discussing their properties, and exploring where this seemingly simple equation might appear in more complex mathematical scenarios. We'll also explore the practical applications of understanding factor pairs and how this knowledge can be helpful in various fields.
Understanding Factors and Factor Pairs
Before we delve into the specific factors of 52, let's clarify the terminology. A factor is a number that divides another number without leaving a remainder. A factor pair consists of two numbers that, when multiplied together, produce a given number. For example, in the equation 2 x 6 = 12, 2 and 6 are a factor pair of 12.
Finding the factors of a number is a fundamental skill in mathematics. It forms the basis for many more advanced concepts, including simplifying fractions, solving equations, and understanding prime numbers.
Finding the Factor Pairs of 52
To determine what numbers multiply to 52, we need to find all its factor pairs. We can do this systematically:
-
Start with 1: Since 1 is a factor of every number, we know that 1 x 52 = 52. This gives us our first factor pair: (1, 52).
-
Check for 2: Since 52 is an even number, it's divisible by 2. 52 / 2 = 26, giving us the factor pair (2, 26).
-
Check for 3: 52 is not divisible by 3 (the sum of its digits, 5 + 2 = 7, is not divisible by 3).
-
Check for 4: 52 / 4 = 13, giving us the factor pair (4, 13).
-
Check for numbers greater than the square root of 52: The square root of 52 is approximately 7.2. Since we've already checked numbers up to 4, and we found their corresponding pairs (13, 4 and 26,2), we've found all factor pairs.
Therefore, the factor pairs of 52 are:
- (1, 52)
- (2, 26)
- (4, 13)
Prime Factorization of 52
The prime factorization of a number is expressing it as a product of only prime numbers (numbers divisible only by 1 and themselves). This is a unique representation for every number. To find the prime factorization of 52:
-
We start with the smallest prime number, 2. 52 is divisible by 2, giving us 2 x 26.
-
26 is also divisible by 2, giving us 2 x 13.
-
13 is a prime number.
Therefore, the prime factorization of 52 is 2 x 2 x 13 or 2² x 13. This representation is unique to 52 and is useful in many mathematical operations.
Applications of Understanding Factors in Mathematics
The ability to find the factors of a number is crucial for various mathematical concepts and applications:
-
Simplifying Fractions: To simplify a fraction, you need to find the greatest common factor (GCF) of the numerator and denominator. For example, if you have the fraction 26/52, finding that the GCF is 26 allows you to simplify it to 1/2.
-
Solving Equations: Factorization is a key technique in solving quadratic equations and other polynomial equations. Understanding factors helps in breaking down complex expressions into simpler ones.
-
Algebraic Manipulation: Many algebraic manipulations, such as expanding and factoring expressions, rely heavily on the understanding of factors.
-
Number Theory: The study of prime numbers and their properties relies extensively on the concepts of factors and factorization.
Applications Beyond Pure Mathematics
The concept of factors and factor pairs extends beyond the realm of pure mathematics and finds applications in various fields:
-
Computer Science: In cryptography, understanding prime factorization is crucial for secure encryption methods. The difficulty in factoring large numbers into their prime components forms the basis of many encryption algorithms.
-
Geometry and Measurement: Calculating areas, volumes, and other geometric properties often involves finding factors and multiples of numbers.
-
Engineering and Design: Many engineering and design problems involve optimization, which often requires finding factors to determine the most efficient solutions.
-
Data Analysis and Statistics: Understanding factors helps in data organization, grouping, and analysis. For example, you might need to divide a dataset into equal groups based on certain factors.
-
Everyday Life: From dividing a pizza equally among friends to planning events, understanding factors and multiples plays a role in everyday situations requiring efficient allocation or fair distribution of resources.
Extending the Concept: Equations Involving 52
The simple equation "what times what equals 52" can be expanded into more complex mathematical problems. For instance:
-
Quadratic Equations: A quadratic equation might include 52 as a constant term. Solving this equation would require factoring or using the quadratic formula, both of which rely on understanding the factors of 52. Example: x² + 17x + 52 = 0. Factoring this equation yields (x+4)(x+13)=0, resulting in solutions x=-4 and x=-13
-
Diophantine Equations: These equations involve finding integer solutions. An example might be finding integer solutions for x and y in the equation xy = 52. The factor pairs of 52 directly provide the integer solutions.
-
Modular Arithmetic: In modular arithmetic, understanding the factors of 52 could be relevant in finding solutions to congruences.
-
Number Patterns and Sequences: The factors of 52 could be part of a larger number pattern or sequence, requiring an understanding of their relationships and properties to predict further terms.
Conclusion:
The seemingly simple question "what times what equals 52?" opens a window into a vast world of mathematical concepts and applications. Understanding factors, factor pairs, and prime factorization is a foundational skill with far-reaching implications, not just in mathematics but also in various other fields. This exploration demonstrates how even the most basic mathematical concepts can have profound implications and connections to more complex areas of study, highlighting the interconnectedness and beauty of mathematics. By appreciating the depth of seemingly simple problems, we can develop a stronger mathematical foundation and a deeper appreciation for the elegance and power of mathematical principles.
Latest Posts
Latest Posts
-
How Much Is 120 Minutes
Sep 16, 2025
-
All Physicians Take Money Mnemonic
Sep 16, 2025
-
E Value Of Boric Acid
Sep 16, 2025
-
Experiment 5 Post Lab Questions
Sep 16, 2025
-
55 To The Nearest 10
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 52 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.