What Times What Equals 81
gasmanvison
Sep 11, 2025 · 4 min read
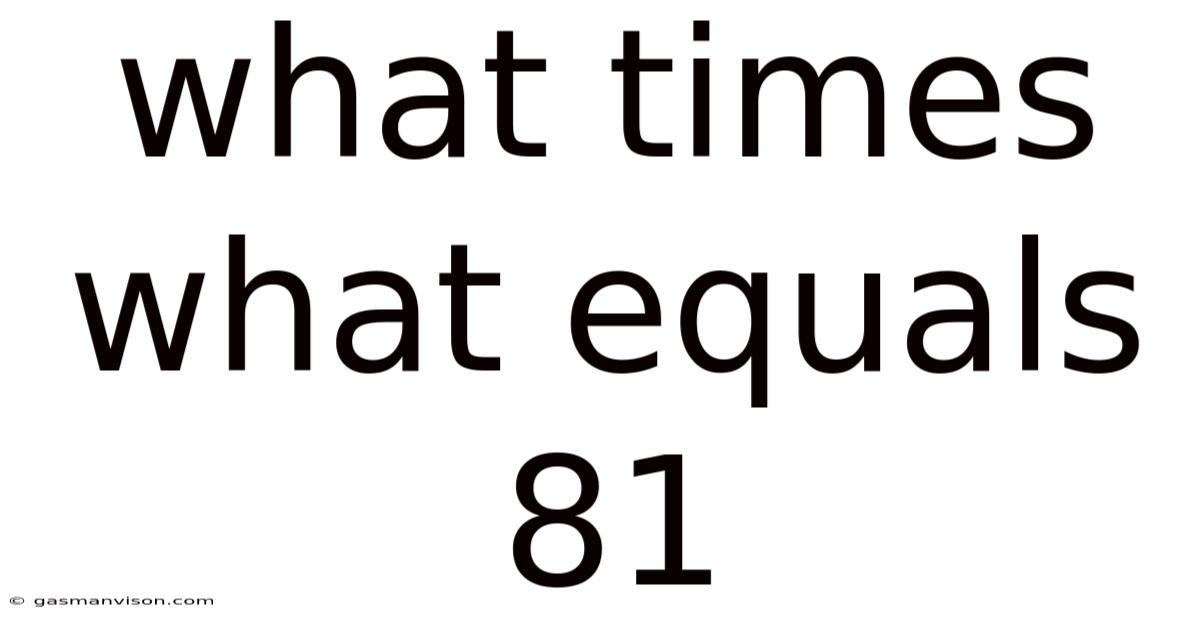
Table of Contents
What Times What Equals 81? Exploring Factors, Prime Factorization, and More
What times what equals 81? This seemingly simple question opens the door to a fascinating exploration of number theory, factorization, and mathematical problem-solving. While the immediate answer might seem obvious to some (9 x 9), a deeper dive reveals a richer understanding of factors, prime numbers, and even the concept of negative numbers. This article will delve into these aspects, providing a comprehensive answer that goes beyond the basic multiplication.
Meta Description: Discover the multiple solutions to the equation "What times what equals 81?" We explore factors, prime factorization, negative numbers, and even touch upon advanced mathematical concepts related to this seemingly simple question.
Finding the factors of 81 involves determining all the numbers that, when multiplied together, result in 81. The most straightforward answer is 9 x 9, representing the square root of 81. However, let's consider other possibilities:
Integer Factors of 81
-
Positive Integers: The positive integer factors of 81 are 1, 3, 9, 27, and 81. These numbers can be paired to produce 81 through multiplication:
- 1 x 81 = 81
- 3 x 27 = 81
- 9 x 9 = 81
-
Negative Integers: Expanding our search to include negative integers reveals additional solutions. Since a negative number multiplied by a negative number results in a positive number, we also have:
- -1 x -81 = 81
- -3 x -27 = 81
- -9 x -9 = 81
This demonstrates that the equation "What times what equals 81?" has multiple solutions, encompassing both positive and negative integer pairs.
Prime Factorization of 81
Understanding the prime factorization of a number helps us break it down into its fundamental building blocks. Prime numbers are whole numbers greater than 1 that have only two divisors: 1 and themselves. The prime factorization of 81 reveals the prime numbers that, when multiplied, equal 81.
To find the prime factorization of 81, we can use a factor tree:
81 is divisible by 3: 81 = 3 x 27
27 is also divisible by 3: 27 = 3 x 9
9 is divisible by 3: 9 = 3 x 3
Therefore, the prime factorization of 81 is 3 x 3 x 3 x 3, or 3⁴. This means that 81 is a perfect power of 3. Knowing the prime factorization is crucial in various mathematical operations, including finding the greatest common divisor (GCD) and the least common multiple (LCM) of numbers.
Beyond Integer Solutions: Fractional and Decimal Factors
The search for solutions to "What times what equals 81?" isn't limited to integers. We can extend our search to include fractions and decimals. For example:
- 27/3 x 9 = 81
- 1/9 x 729 = 81
- 0.1 x 810 = 81
- 18 x 4.5 = 81
and countless other fractional and decimal combinations. The possibilities become infinitely large when considering all possible rational and irrational numbers.
Applications and Real-World Examples
Understanding factors and factorization isn't just an abstract mathematical exercise. It has practical applications in various fields:
-
Geometry: Calculating the area of a square with an area of 81 square units directly uses the concept of finding the square root. The side length would be 9 units (9 x 9 = 81).
-
Algebra: Solving quadratic equations often involves finding factors to simplify expressions. For example, the equation x² - 81 = 0 can be factored as (x - 9)(x + 9) = 0, leading to solutions x = 9 and x = -9.
-
Computer Science: Factorization plays a critical role in cryptography. The security of many encryption algorithms relies on the difficulty of factoring very large numbers into their prime factors.
-
Data Analysis: In data analysis, factorization techniques are used for dimensionality reduction and feature extraction in large datasets.
Expanding the Question: More Complex Variations
We can make the initial question more complex by adding constraints or altering the nature of the equation. For instance:
-
What two consecutive numbers add up to 81? This requires a different approach, using algebra to solve the equation x + (x+1) = 81.
-
What three numbers, when multiplied, equal 81? This opens up a wider range of possibilities. For example, 3 x 3 x 9 = 81, or 1 x 9 x 9 = 81.
-
What two numbers, when multiplied, equal 81 and their sum is 20? This combines multiplication and addition, leading to a more complex problem-solving process requiring systems of equations.
These variations highlight how a seemingly simple question can lead to more intricate mathematical explorations.
Conclusion: The Richness of a Simple Equation
The question "What times what equals 81?" might appear trivial at first glance, but its exploration reveals a wealth of mathematical concepts. From basic multiplication to prime factorization, from integer solutions to fractional and decimal solutions, and finally to the applications in various fields, the question acts as a springboard to a deeper understanding of number theory and its practical significance. Understanding the factors and prime factorization of numbers is fundamental to more advanced mathematical concepts and has wide-ranging applications in diverse disciplines. The simple question demonstrates the underlying complexity and richness even within the most elementary mathematical inquiries. So next time you encounter a seemingly simple arithmetic problem, remember to explore the possibilities beyond the immediate answer. You might discover surprising depth and connections.
Latest Posts
Latest Posts
-
58 Degrees Fahrenheit To Celsius
Sep 11, 2025
-
How Was Persian Coinage Sophisticated
Sep 11, 2025
-
Summarizing Can Be Used To
Sep 11, 2025
-
Which Statement Best Describes Succession
Sep 11, 2025
-
New Kid Summary Of Chapters
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Times What Equals 81 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.