Whats 25 Percent Of 40
gasmanvison
Sep 01, 2025 · 6 min read
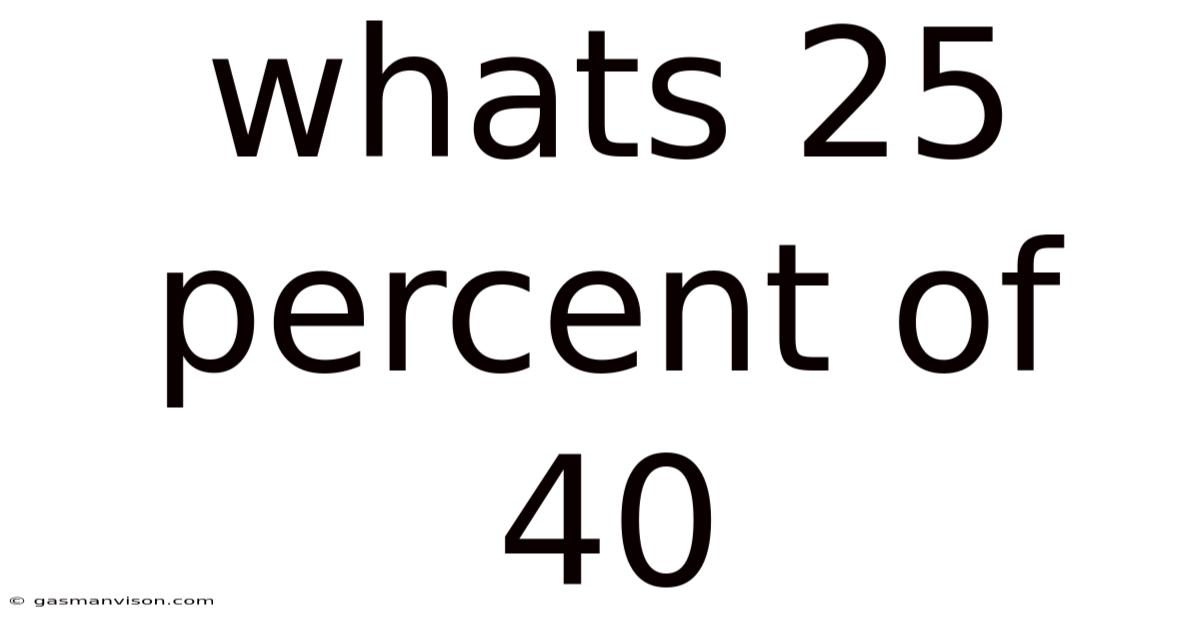
Table of Contents
What's 25 Percent of 40? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What's 25 percent of 40?", opens a door to a world of mathematical concepts with far-reaching applications in everyday life, finance, and various professional fields. This article will not only answer the question directly but will also delve into the underlying principles of percentage calculations, explore different methods for solving percentage problems, and showcase practical examples to solidify your understanding. By the end, you'll be equipped to confidently tackle any percentage calculation you encounter.
Meta Description: Learn how to calculate 25% of 40 and master percentage calculations. This comprehensive guide explains different methods, provides real-world examples, and explores the significance of percentages in various fields.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." Understanding this fundamental concept is crucial for grasping percentage calculations. The percentage symbol (%) is used to represent a percentage. So, 25% means 25 out of 100, which can be written as a fraction (25/100) or a decimal (0.25).
Calculating 25% of 40: Three Different Approaches
There are several ways to calculate 25% of 40. Let's explore three common methods:
1. The Fraction Method:
This method leverages the fractional representation of a percentage. Since 25% is equivalent to 25/100, we can rewrite the problem as:
(25/100) * 40
Simplifying the fraction, we get:
(1/4) * 40 = 10
Therefore, 25% of 40 is 10.
2. The Decimal Method:
This method uses the decimal equivalent of a percentage. As mentioned earlier, 25% is equal to 0.25. The calculation becomes:
0.25 * 40 = 10
This method is often preferred for its simplicity and ease of use, especially with calculators.
3. The Proportion Method:
This method sets up a proportion to solve for the unknown value. We can represent the problem as:
25/100 = x/40
To solve for x (25% of 40), we cross-multiply:
25 * 40 = 100 * x
1000 = 100x
x = 1000/100 = 10
This method is particularly useful for understanding the relationship between percentages and their corresponding values. It’s a more formal approach, often taught in introductory algebra.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of life. Here are some examples:
-
Sales and Discounts: Stores frequently advertise discounts as percentages. For example, a 20% discount on a $50 item means you save 20% of $50, which is $10, resulting in a final price of $40.
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages of the taxable amount. Understanding percentage calculations is vital for determining the tax liability accurately.
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Calculating interest earned or paid requires a solid understanding of percentage calculations. Compound interest, where interest is calculated on both the principal and accumulated interest, involves more complex percentage calculations.
-
Tips and Gratuities: Calculating tips in restaurants or service charges often involves determining a percentage of the bill. A common tip is 15% or 20% of the total bill.
-
Profit Margins: Businesses use percentage calculations to determine their profit margins, which represent the percentage of revenue that remains as profit after deducting all expenses.
-
Statistical Analysis: Percentages are extensively used in statistical analysis to represent proportions, frequencies, and changes in data. For example, expressing survey results as percentages provides a clear and concise way to understand the distribution of responses.
-
Financial Reporting: Financial statements, such as income statements and balance sheets, use percentages to show the relationship between different financial items. For example, the gross profit margin is expressed as a percentage of revenue.
-
Grade Calculations: In education, grades are often expressed as percentages to indicate a student's performance on an assignment or exam.
-
Growth Rates: Businesses and economists use percentage change to calculate growth rates in sales, profits, or economic indicators. This helps track performance over time.
Advanced Percentage Calculations: Beyond the Basics
While calculating 25% of 40 is relatively straightforward, more complex percentage problems may involve:
-
Finding the Percentage: Instead of calculating a percentage of a number, you might need to find what percentage one number is of another. For example, what percentage of 80 is 20? This involves dividing 20 by 80 and multiplying by 100.
-
Finding the Original Amount: You might know the percentage and the resulting value, but need to determine the original amount. For instance, if a discounted price is $60 after a 25% discount, what was the original price? This involves setting up an equation to solve for the original price.
-
Percentage Increase/Decrease: Calculating the percentage increase or decrease between two numbers is another common application. For instance, if sales increased from $100 to $120, the percentage increase is calculated as [(120-100)/100] * 100 = 20%.
-
Compound Interest Calculations: This involves calculating interest on both the principal and accumulated interest. The formula for compound interest is A = P (1 + r/n)^(nt), where A is the final amount, P is the principal amount, r is the annual interest rate, n is the number of times that interest is compounded per year, and t is the number of years.
Mastering Percentage Calculations: Tips and Tricks
Here are some helpful tips and tricks for mastering percentage calculations:
-
Memorize Common Percentages: Familiarizing yourself with the fractional and decimal equivalents of common percentages (like 10%, 25%, 50%, 75%) will significantly speed up your calculations.
-
Use a Calculator: For more complex calculations, a calculator is an invaluable tool. Many calculators have a percentage function that simplifies the process.
-
Practice Regularly: The best way to master percentage calculations is through consistent practice. Work through various examples, starting with simple problems and gradually progressing to more challenging ones.
-
Understand the Concepts: Don't just memorize formulas; understand the underlying principles of percentages and their applications. This will help you adapt to different problem-solving scenarios.
-
Break Down Complex Problems: If faced with a complex percentage problem, break it down into smaller, more manageable steps. This will make the problem less daunting and easier to solve.
Conclusion: The Power of Percentages
The seemingly simple question, "What's 25 percent of 40?", has served as a springboard to explore the vast world of percentage calculations. From basic arithmetic to advanced financial applications, understanding percentages is essential for navigating various aspects of daily life and professional fields. By mastering the methods presented and consistently practicing, you'll not only be able to calculate 25% of 40 effortlessly but also tackle more complex percentage problems with confidence. Remember, the key is to understand the underlying principles and to apply the appropriate method based on the specific problem at hand. So, go forth and conquer the world of percentages!
Latest Posts
Latest Posts
-
Who Is Necas Policy Making Body
Sep 02, 2025
-
Reversible Lanes Are Marked With
Sep 02, 2025
-
When Do Bytes Become Meaningful
Sep 02, 2025
-
According To Objectivism Man Exists
Sep 02, 2025
-
How Is Johnsons Approach Innovative
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about Whats 25 Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.