Whats 30 Percent Of 80
gasmanvison
Sep 04, 2025 · 5 min read
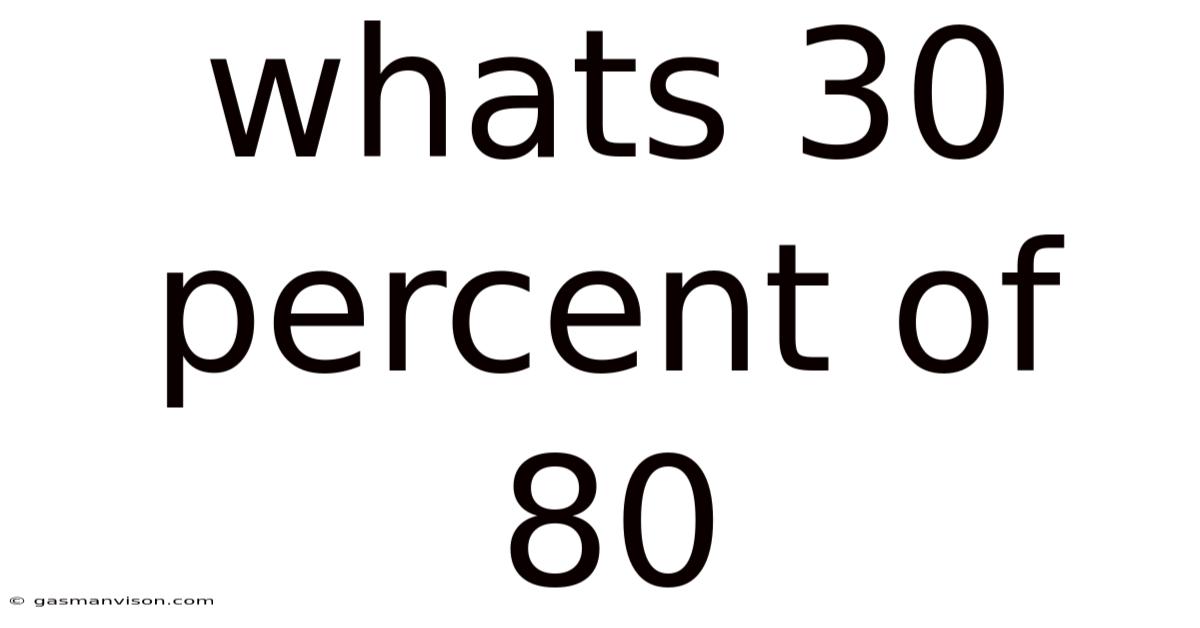
Table of Contents
What's 30 Percent of 80? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What's 30 percent of 80?", opens a door to a vast world of mathematical concepts and practical applications. While the answer itself is straightforward (24), understanding the underlying principles and exploring various methods for calculating percentages is crucial for navigating numerous real-world scenarios. This article will not only provide the solution but also delve into the intricacies of percentage calculations, explore different approaches, and highlight their relevance in various fields.
Meta Description: Learn how to calculate 30% of 80 and master percentage calculations. This comprehensive guide explores various methods, real-world applications, and the importance of percentages in everyday life and various professions.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" – "per cent" being derived from the Latin per centum. Therefore, 30 percent (30%) means 30 out of 100, or 30/100, which simplifies to 3/10. Understanding this fundamental concept is vital for tackling percentage problems.
Calculating 30% of 80: Three Primary Methods
There are several ways to calculate 30% of 80. Let's explore three common methods:
1. The Fraction Method:
This method leverages the fractional representation of a percentage. As mentioned, 30% is equivalent to 30/100. To find 30% of 80, we multiply 80 by the fraction 30/100:
(30/100) * 80 = 24
This method is conceptually straightforward and easy to understand, especially for beginners. It emphasizes the underlying fractional nature of percentages.
2. The Decimal Method:
This approach converts the percentage into its decimal equivalent. To convert a percentage to a decimal, divide the percentage by 100. Therefore, 30% becomes 0.30 (or simply 0.3). We then multiply this decimal by the number:
0.3 * 80 = 24
This method is efficient and widely used due to its simplicity and compatibility with calculators. It's particularly helpful when dealing with more complex percentage calculations.
3. The Proportion Method:
This method sets up a proportion to solve for the unknown value. We can represent the problem as:
30/100 = x/80
Where 'x' represents the unknown value (30% of 80). To solve for x, we cross-multiply:
30 * 80 = 100 * x 2400 = 100x x = 2400/100 x = 24
The proportion method is a more formal approach, often used in mathematical contexts and provides a clear structure for solving percentage problems.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a fundamental skill applicable across numerous fields. Here are a few examples:
-
Finance and Business: Calculating profits, losses, discounts, interest rates, taxes, and investment returns all rely heavily on percentage calculations. Understanding percentage change is crucial for analyzing financial trends and making informed decisions. For example, a business might need to calculate the percentage increase in sales year-over-year or determine the percentage discount to offer during a sale. Knowing that a 30% discount on an $80 item results in a $24 discount and a final price of $56 is critical for pricing strategies.
-
Sales and Marketing: Discounts, markups, sales tax calculations, commission structures, and conversion rates all involve percentages. Marketing campaigns often use percentage-based metrics to measure success. For instance, analyzing click-through rates (CTR) or conversion rates necessitates percentage calculations to understand campaign effectiveness.
-
Science and Statistics: Percentages are fundamental in expressing probabilities, representing data in charts and graphs (like pie charts), and performing statistical analysis. Scientific experiments often involve calculating percentages to represent the proportion of successful trials or the frequency of observed events.
-
Everyday Life: Tip calculations in restaurants, figuring out sales tax on purchases, determining the percentage of a task completed, and calculating interest on loans are everyday examples of situations where percentage knowledge is essential. Understanding discounts allows consumers to make informed buying decisions, and calculating tips ensures fair compensation for services.
-
Education: Percentages are used extensively in grading systems, calculating test scores, and expressing the proportion of students achieving certain academic milestones. Understanding percentage-based grading systems helps students track their progress and teachers assess student performance.
Advanced Percentage Calculations: Beyond the Basics
While calculating 30% of 80 is straightforward, understanding more complex percentage scenarios is valuable. Let's explore some examples:
- Finding the Original Value: If an item is on sale for $56 after a 30% discount, what was the original price? This requires working backward using the percentage and the discounted price. Let's say 'x' is the original price:
x - 0.3x = 56 0.7x = 56 x = 56 / 0.7 x = 80
- Percentage Increase/Decrease: Calculating the percentage change between two values requires understanding the difference and relating it to the original value. For example, if sales increased from 80 units to 104 units, the percentage increase is calculated as:
((104 - 80) / 80) * 100 = 30%
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. Compound interest calculations require understanding exponential growth, making it a more advanced application of percentage calculations.
-
Percentage Points vs. Percentages: It's crucial to distinguish between percentage points and percentages. A change from 20% to 50% is a 30 percentage point increase, but a 150% increase in percentage terms.
Mastering Percentages: Tips and Tricks
-
Practice Regularly: The more you practice percentage calculations, the more comfortable and efficient you'll become. Start with simple problems and gradually increase the complexity.
-
Use a Calculator: Calculators can significantly speed up the process, especially for complex calculations.
-
Understand the Concepts: Focusing on the underlying principles of percentages, fractions, and decimals will improve your understanding and problem-solving abilities.
-
Check Your Work: Always double-check your calculations to ensure accuracy. Using multiple methods can help verify the results.
-
Seek Help When Needed: Don't hesitate to seek clarification or assistance if you encounter difficulties. There are numerous online resources and educational materials available.
Conclusion: The Enduring Relevance of Percentages
The seemingly simple question of "What's 30 percent of 80?" provides a gateway to understanding the profound significance of percentages in our daily lives and various professional fields. Mastering percentage calculations is not just a mathematical skill; it's a practical tool that empowers informed decision-making, analysis, and problem-solving across a wide spectrum of domains. By understanding the various methods of calculation and their applications, individuals can enhance their analytical capabilities and navigate the numerical world with greater confidence and competence. The seemingly simple answer – 24 – unlocks a world of practical applications and mathematical understanding.
Latest Posts
Latest Posts
-
Classical Conditioning Examples Everyday Life
Sep 07, 2025
-
Longitudinal Section Vs Cross Section
Sep 07, 2025
-
What Was A Pilgrimage Road
Sep 07, 2025
-
Louis Armstrong Lyrics Wonderful World
Sep 07, 2025
-
Formula For Aluminum And Carbonate
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about Whats 30 Percent Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.