Whats 60 Percent Of 30
gasmanvison
Sep 21, 2025 · 4 min read
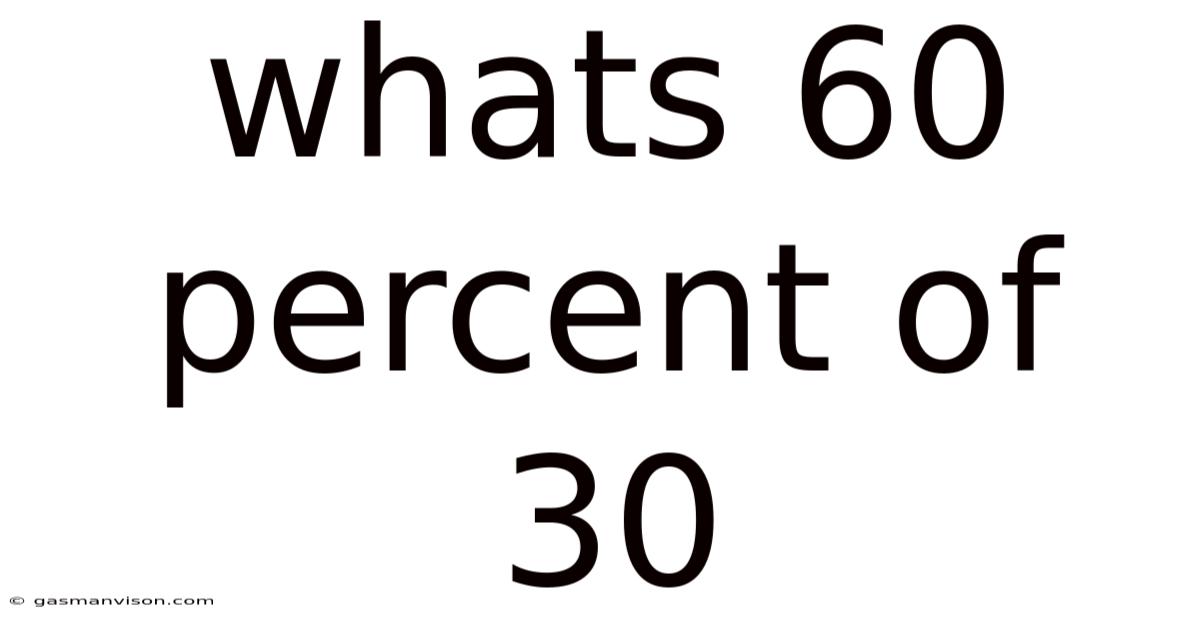
Table of Contents
What's 60 Percent of 30? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What's 60 percent of 30?", opens a door to a vast world of mathematical concepts and practical applications. While the answer itself is straightforward – 18 – the journey to understanding how to arrive at that answer, and the broader implications of percentage calculations, is far more enriching. This article will not only solve the problem but also explore the underlying principles, provide various methods for solving percentage problems, and delve into the numerous real-world scenarios where percentage calculations are essential.
Understanding Percentages: The Building Blocks
Before we tackle the specific problem, let's establish a firm grasp of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100". Therefore, 60% means 60 out of 100, or 60/100, which simplifies to 3/5. This fractional representation is key to understanding how percentages work.
Method 1: The Direct Calculation Method
The most straightforward way to calculate 60% of 30 is to convert the percentage to a decimal and multiply:
- Convert the percentage to a decimal: 60% = 60/100 = 0.60
- Multiply the decimal by the number: 0.60 * 30 = 18
Therefore, 60% of 30 is 18. This method is efficient and easily adaptable to various percentage calculations.
Method 2: The Fractional Method
As mentioned earlier, 60% can be expressed as the fraction 3/5. Using this fractional representation provides an alternative solution:
- Express the percentage as a fraction: 60% = 3/5
- Multiply the fraction by the number: (3/5) * 30 = (3 * 30) / 5 = 90 / 5 = 18
This method highlights the relationship between percentages, fractions, and decimals, offering a deeper understanding of the underlying mathematical principles.
Method 3: Using Proportions
Proportions offer a more visual and intuitive approach to solving percentage problems. We can set up a proportion to solve for the unknown value (x):
60/100 = x/30
To solve this proportion, we cross-multiply:
60 * 30 = 100 * x 1800 = 100x x = 1800 / 100 x = 18
This method is particularly useful when dealing with more complex percentage problems or when visualizing the relationship between the parts and the whole.
Real-World Applications of Percentage Calculations
Understanding percentages is crucial in numerous real-life situations. Here are some examples:
- Sales and Discounts: Calculating discounts on sale items. For instance, a 20% discount on a $50 item means a saving of $10 (20% of $50).
- Taxes and Interest: Determining the amount of sales tax or interest on a loan or investment. A 5% sales tax on a $100 purchase adds $5 to the total cost.
- Financial Analysis: Analyzing financial statements, calculating profit margins, and understanding growth rates. A company's profit margin is often expressed as a percentage of revenue.
- Statistics and Data Analysis: Representing data in charts and graphs, calculating percentages of different groups within a population. For example, expressing survey results as percentages.
- Scientific Calculations: Calculating concentrations of solutions, expressing the efficiency of processes, and interpreting experimental results.
- Everyday Life: Calculating tips in restaurants, understanding the nutritional information on food labels (e.g., percentage of daily value), and comparing prices.
Beyond the Basics: More Complex Percentage Problems
While the problem "What's 60 percent of 30?" is relatively simple, the principles extend to more complex scenarios. Here are some examples:
- Finding the Percentage: If you know the part and the whole, you can calculate the percentage. For example, if 12 out of 30 students passed an exam, the percentage of students who passed is (12/30) * 100% = 40%.
- Finding the Whole: If you know the percentage and the part, you can calculate the whole. For example, if 25% of a number is 10, the whole number is 10 / (25/100) = 40.
- Percentage Increase and Decrease: Calculating percentage changes over time. For example, if a stock price increases from $50 to $60, the percentage increase is [(60-50)/50] * 100% = 20%.
- Compound Interest: Calculating interest earned on an investment where the interest is added to the principal amount each period. This involves repeated percentage calculations.
Tips and Tricks for Solving Percentage Problems
Here are some helpful tips to master percentage calculations:
- Memorize common percentage equivalents: Knowing that 25% = 1/4, 50% = 1/2, and 75% = 3/4 can greatly simplify calculations.
- Use a calculator: For more complex problems, a calculator can save time and ensure accuracy.
- Practice regularly: Consistent practice is key to mastering percentage calculations and building confidence.
- Break down complex problems: Divide complex problems into smaller, manageable steps.
- Check your answers: Always double-check your calculations to avoid errors.
Conclusion: The Power of Percentages
The seemingly simple question, "What's 60 percent of 30?", has served as a springboard to explore the fascinating world of percentages and their applications. From everyday calculations to complex financial analyses, understanding percentages is a fundamental skill with far-reaching implications. By mastering the different methods of calculation and understanding the underlying principles, you'll be well-equipped to tackle any percentage problem you encounter. Remember to practice regularly, and you'll soon find these calculations become second nature. The ability to confidently work with percentages is a valuable asset in both personal and professional life.
Latest Posts
Latest Posts
-
How Much Is 72 Kg
Sep 21, 2025
-
15kg Is How Many Pounds
Sep 21, 2025
-
Political Party In A Sentence
Sep 21, 2025
-
3 Is 25 Of What
Sep 21, 2025
-
How Did Ponyboys Parents Die
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Whats 60 Percent Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.