Whats Half Of 2 1/2
gasmanvison
Sep 14, 2025 · 5 min read
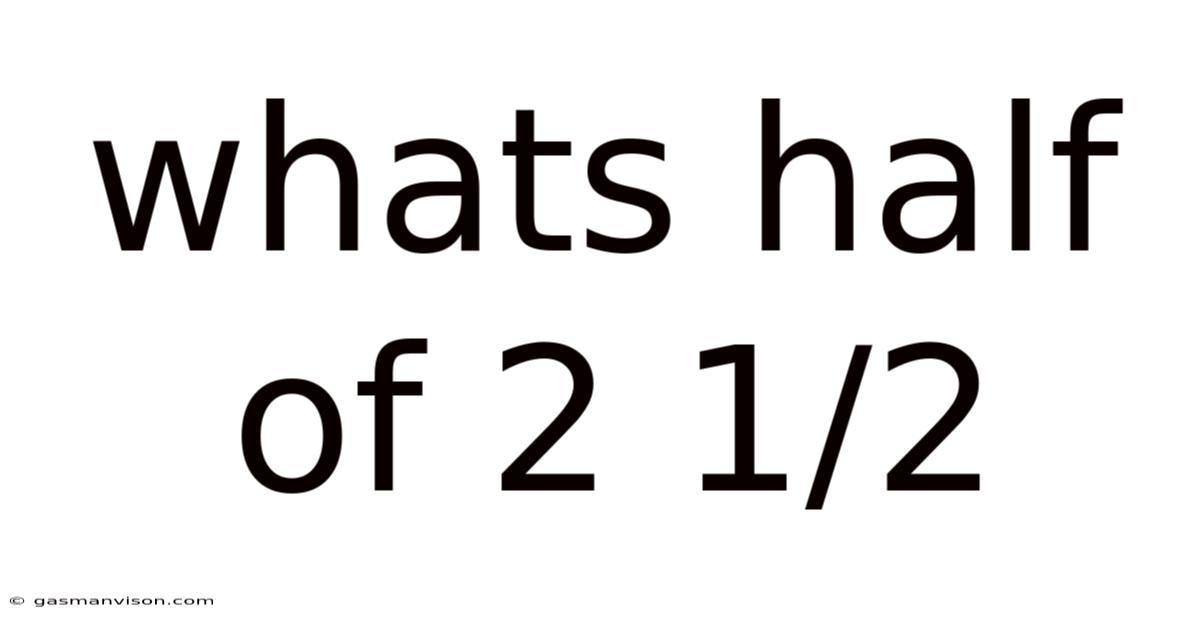
Table of Contents
What's Half of 2 1/2? A Deep Dive into Fractions and Their Applications
What's half of 2 1/2? This seemingly simple question opens the door to a fascinating exploration of fractions, their manipulation, and their surprisingly widespread applications in everyday life. While the answer itself is straightforward, understanding the how behind the answer unlocks a deeper understanding of mathematical principles crucial for various fields, from cooking and construction to advanced scientific calculations. This article will not only provide the solution but delve into the methods, the underlying concepts, and the broader significance of fractional arithmetic.
Understanding Fractions: A Quick Refresher
Before we tackle the core question, let's quickly review the basics of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many equal parts the whole is divided into. For example, 1/2 represents one out of two equal parts, while 3/4 represents three out of four equal parts.
Methods for Calculating Half of 2 1/2
There are several ways to calculate half of 2 1/2, each offering a slightly different approach and showcasing various aspects of fractional arithmetic. Let's explore three common methods:
Method 1: Converting to an Improper Fraction
This method involves converting the mixed number (2 1/2) into an improper fraction. An improper fraction is one where the numerator is greater than or equal to the denominator.
-
Convert the mixed number to an improper fraction: To do this, multiply the whole number (2) by the denominator (2), add the numerator (1), and keep the same denominator. This gives us (2 * 2) + 1 = 5/2.
-
Find half of the improper fraction: To find half of 5/2, we multiply it by 1/2: (5/2) * (1/2) = 5/4.
-
Simplify (if necessary): The fraction 5/4 is an improper fraction. We can convert it back to a mixed number by dividing the numerator (5) by the denominator (4). This gives us 1 with a remainder of 1, so the answer is 1 1/4.
Method 2: Working with the Whole Number and Fraction Separately
This method involves dividing the whole number and fractional parts separately before combining the results.
-
Find half of the whole number: Half of 2 is 1.
-
Find half of the fraction: Half of 1/2 is (1/2) * (1/2) = 1/4.
-
Combine the results: Add the results from steps 1 and 2: 1 + 1/4 = 1 1/4.
Method 3: Using Decimal Representation
This method involves converting the mixed number to a decimal and then performing the calculation.
-
Convert the mixed number to a decimal: 2 1/2 is equal to 2.5.
-
Find half of the decimal: Half of 2.5 is 2.5 / 2 = 1.25.
-
Convert back to a fraction (optional): 1.25 can be expressed as 1 1/4.
Therefore, half of 2 1/2 is 1 1/4.
Real-World Applications of Fractional Arithmetic
The seemingly simple calculation of half of 2 1/2 has far-reaching applications in various aspects of daily life. Consider these examples:
-
Cooking and Baking: Recipes often require precise measurements. Scaling down a recipe might involve halving ingredients, requiring a firm understanding of fractions. For instance, if a recipe calls for 2 1/2 cups of flour, halving it would require 1 1/4 cups.
-
Construction and Engineering: Accurate measurements are crucial in construction. Calculations involving lengths, widths, and volumes often involve fractions, particularly when dealing with materials like lumber or concrete. Imagine calculating the amount of paint needed for half of a 2 1/2 meter wall.
-
Finance and Budgeting: Understanding fractions is essential for managing personal finances. Calculating discounts, interest rates, or proportions of budgets often involves working with fractions or percentages (which are essentially fractions).
-
Data Analysis and Statistics: Many statistical calculations involve fractions. For example, calculating proportions, means, and medians often requires manipulating fractions.
-
Science and Technology: Fractions are fundamental in numerous scientific disciplines, from physics and chemistry to computer science and engineering. Calculations related to measurements, ratios, and proportions are common.
Beyond the Basics: Further Exploration of Fractions
This seemingly simple question has led us to explore various aspects of fractions. But the journey doesn't end here. Further exploration could encompass:
-
Different types of fractions: Understanding the distinctions between proper fractions, improper fractions, and mixed numbers is crucial for efficient calculations.
-
Fraction operations: Mastering addition, subtraction, multiplication, and division of fractions is essential for solving more complex problems.
-
Converting between fractions, decimals, and percentages: The ability to seamlessly convert between these representations allows for greater flexibility and efficiency in problem-solving.
-
Advanced applications: Exploring the application of fractions in calculus, algebra, and other advanced mathematical fields reveals their profound significance in understanding complex systems.
Conclusion: The Power of Understanding Fractions
The question "What's half of 2 1/2?" might seem trivial at first glance. However, its answer unveils a wealth of mathematical concepts with far-reaching implications. Mastering fractional arithmetic is not just about solving mathematical problems; it's about developing a fundamental understanding of ratios, proportions, and measurements—skills crucial for navigating the complexities of everyday life and unlocking success in various fields. From the kitchen to the construction site, from the boardroom to the laboratory, the ability to work confidently with fractions is a valuable asset. Understanding the "how" behind the seemingly simple answer of 1 1/4 opens doors to a deeper appreciation for the power and versatility of fractions.
Latest Posts
Latest Posts
-
Universal Precautions Require Employees To
Sep 14, 2025
-
2 4 9 Divided By 11 9
Sep 14, 2025
-
Algebra 1 Big Ideas Answers
Sep 14, 2025
-
Lewis Dot Structure For Sef5
Sep 14, 2025
-
Topic 2 Assessment Form A
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Whats Half Of 2 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.