What's Half Of 2 3
gasmanvison
Sep 23, 2025 · 5 min read
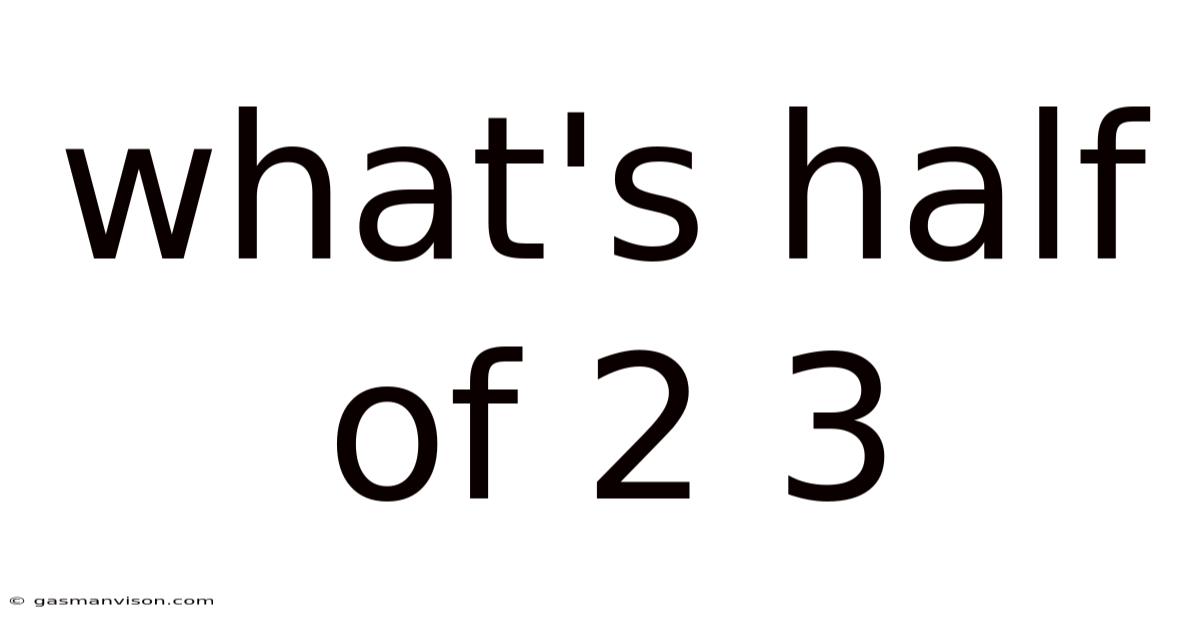
Table of Contents
What's Half of 2/3? A Deep Dive into Fractions and Beyond
This seemingly simple question, "What's half of 2/3?", opens the door to a fascinating exploration of fractions, mathematical operations, and their practical applications. While the answer itself is straightforward, understanding the why behind the calculation is crucial for developing a strong foundation in mathematics. This article will not only provide the solution but also delve into the underlying concepts, offering various methods to solve similar problems and demonstrating the relevance of fractions in everyday life.
Meta Description: Learn how to calculate half of 2/3 and master fraction operations. This comprehensive guide explains the process, provides alternative methods, and explores the practical applications of fractions.
Understanding Fractions: The Building Blocks
Before tackling the problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In our problem, 2/3, the numerator is 2 (we have 2 parts), and the denominator is 3 (the whole is divided into 3 equal parts).
Method 1: Direct Multiplication
The most straightforward way to find half of 2/3 is to multiply the fraction by 1/2:
(2/3) x (1/2) = (2 x 1) / (3 x 2) = 2/6
This simplifies to 1/3. Therefore, half of 2/3 is 1/3.
This method highlights the fundamental rule of multiplying fractions: multiply the numerators together and multiply the denominators together. The resulting fraction can then be simplified if possible, as we did by dividing both the numerator and denominator of 2/6 by 2.
Method 2: Dividing by 2 (or Multiplying by the Reciprocal)
Another approach involves directly dividing the fraction 2/3 by 2. Remember that dividing by a whole number is the same as multiplying by its reciprocal. The reciprocal of 2 is 1/2. Thus, we get:
(2/3) ÷ 2 = (2/3) x (1/2) = 2/6 = 1/3
This method reinforces the connection between division and multiplication with fractions, emphasizing that division is essentially the inverse operation of multiplication. This understanding is vital for tackling more complex fractional calculations.
Method 3: Visual Representation
Visualizing fractions can greatly aid understanding, particularly for those who prefer a more intuitive approach. Imagine a circle divided into three equal parts. If we shade two of these parts, we represent the fraction 2/3. To find half of this shaded area, we simply divide the shaded portion into two equal parts. Each of these smaller parts represents 1/3 of the whole circle.
Simplifying Fractions: A Crucial Step
The process of simplifying fractions, also known as reducing fractions to their lowest terms, involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. In our example, the GCD of 2 and 6 is 2. Dividing both the numerator and denominator by 2 gives us the simplified fraction 1/3. Simplifying fractions is essential for presenting answers in their most concise and understandable form. It also aids in comparing fractions and performing further calculations.
Practical Applications of Fractions
Fractions are not just abstract mathematical concepts; they are essential tools used extensively in daily life:
- Cooking and Baking: Recipes often require fractional measurements of ingredients (e.g., 1/2 cup of flour, 2/3 cup of sugar).
- Construction and Engineering: Accurate measurements and calculations in construction and engineering rely heavily on fractions and decimals, ensuring the structural integrity and functionality of buildings and other structures.
- Finance: Understanding fractions is critical for managing budgets, calculating interest rates, and comprehending financial statements.
- Science: Many scientific measurements and calculations involve fractions, particularly in fields like chemistry and physics, where precise proportions are crucial.
- Time Management: Telling time involves fractions (e.g., a quarter of an hour is 15 minutes, half an hour is 30 minutes).
Extending the Concept: Halving Other Fractions
The methods discussed above can be applied to find half of any fraction. For example, let's find half of 5/8:
(5/8) x (1/2) = 5/16
This fraction is already in its simplest form, as 5 and 16 have no common factors other than 1.
Let's try another example: find half of 3/4:
(3/4) x (1/2) = 3/8
Again, this fraction is in its simplest form.
Dealing with Mixed Numbers
A mixed number combines a whole number and a fraction (e.g., 1 1/2). To find half of a mixed number, you can either convert it to an improper fraction first or find half of the whole number and half of the fraction separately and then combine the results.
Let's find half of 1 1/2:
Method 1: Convert to an improper fraction:
1 1/2 = (2 x 1 + 1)/2 = 3/2
(3/2) x (1/2) = 3/4
Method 2: Find half of each part separately:
Half of 1 is 1/2. Half of 1/2 is 1/4. Therefore, half of 1 1/2 is 1/2 + 1/4 = 3/4
Beyond Halving: Other Fraction Operations
Understanding how to find half of a fraction lays the groundwork for mastering other fraction operations such as addition, subtraction, multiplication, and division. These operations are fundamental to numerous mathematical applications, from solving simple equations to tackling advanced calculus problems. Mastering these operations requires consistent practice and a thorough understanding of the underlying principles.
Conclusion: The Power of Understanding Fractions
The seemingly simple question, "What's half of 2/3?", serves as a gateway to a broader understanding of fractions and their importance in various aspects of life. By mastering the techniques presented in this article, you equip yourself with essential mathematical skills applicable to numerous real-world scenarios. Remember to practice regularly, explore different approaches, and visualize the concepts to solidify your understanding. The ability to confidently manipulate fractions is an invaluable asset, enhancing your problem-solving abilities and contributing to your overall mathematical proficiency. From simple recipes to complex engineering projects, the power of fractions is undeniable.
Latest Posts
Latest Posts
-
10 7w 13 7w 15
Sep 23, 2025
-
Lewis Dot Structure For Alcl3
Sep 23, 2025
-
Lcm Of 8 And 12
Sep 23, 2025
-
A Nurse Assistant Is Attending
Sep 23, 2025
-
What Is Equivalent To 4 12
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What's Half Of 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.