X 2 2x 48 0
gasmanvison
Sep 22, 2025 · 5 min read
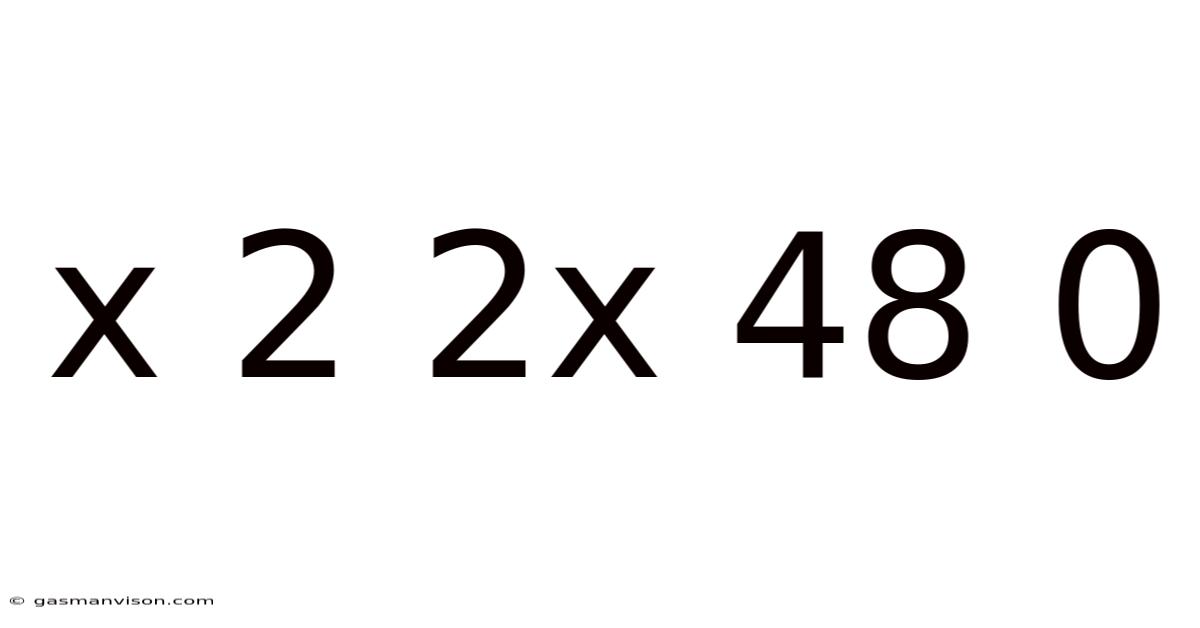
Table of Contents
Decoding the Sequence: x 2 2x 48 0 – A Deep Dive into Pattern Recognition and Problem Solving
This seemingly simple sequence, "x 2 2x 48 0," presents a fascinating challenge in pattern recognition and mathematical problem-solving. At first glance, it appears cryptic. However, by applying logical reasoning, algebraic manipulation, and a systematic approach, we can unravel the underlying pattern and determine the value of 'x'. This article will delve into various methods to solve this puzzle, exploring different perspectives and highlighting the importance of systematic thinking in problem-solving. We'll also touch upon the broader implications of such exercises in developing critical thinking skills.
Understanding the Problem:
The sequence "x 2 2x 48 0" presents a series of numbers and a variable 'x'. The challenge is to identify a consistent mathematical relationship or pattern connecting these elements. The solution requires identifying the operation or series of operations that transform one element into the next. This type of problem is common in mathematical aptitude tests, logic puzzles, and even in advanced fields like cryptography and data analysis.
Method 1: Exploring Arithmetic Progressions and Geometric Progressions
Our initial instinct might be to explore common mathematical progressions. Let's examine whether the sequence follows an arithmetic progression (constant difference between consecutive terms) or a geometric progression (constant ratio between consecutive terms).
-
Arithmetic Progression: The differences between consecutive terms are not constant. (2 - x), (2x - 2), (48 - 2x), (0 - 48). This eliminates the possibility of a simple arithmetic progression.
-
Geometric Progression: Similarly, the ratios between consecutive terms are not constant. (2/x), (2x/2), (48/2x), (0/48). This also rules out a simple geometric progression.
Since neither a simple arithmetic nor geometric progression fits the data, we need to explore more complex patterns and relationships.
Method 2: Investigating Algebraic Relationships
Given the presence of the variable 'x', it's highly likely that an algebraic relationship governs the sequence. We can attempt to establish equations connecting the terms. Let's analyze the potential relationships:
-
Relationship between consecutive terms: We can formulate equations based on the relationships between consecutive terms. However, without a clear pattern, this approach becomes cumbersome and potentially leads to multiple solutions.
-
Focus on the 'x' variable: A more strategic approach would involve focusing on the role of 'x'. It’s likely that 'x' is related to the other numbers in a specific way. Let's experiment with different algebraic expressions involving 'x'.
Method 3: Trial and Error and Systematic Testing
This method involves systematically trying different values of 'x' and observing the resulting sequence. While potentially time-consuming, it offers a hands-on approach to discovering the pattern. Let's try a few values for 'x' and see if we can find a consistent pattern:
-
If x = 1: The sequence becomes: 1 2 2 48 0. No clear pattern emerges.
-
If x = 2: The sequence becomes: 2 2 4 48 0. Still no discernible pattern.
-
If x = 4: The sequence becomes: 4 2 8 48 0. We might start to see a faint pattern of doubling and halving, but it's not consistent.
While trial and error can be helpful, it's not the most efficient approach for complex sequences. A more systematic method is needed.
Method 4: Employing Advanced Algebraic Techniques
We can explore more advanced algebraic techniques to solve this puzzle. One possible approach is to consider polynomial relationships. This involves fitting a polynomial equation to the given data points. However, fitting a polynomial to only four data points with a variable 'x' requires significant assumptions and leads to potentially numerous solutions. Therefore, we must carefully examine the constraints imposed by the limited data set.
Method 5: Considering a Piecewise Function
Given that the sequence is short and doesn’t seem to fit a single, simple equation, it's possible that a piecewise function is at play. A piecewise function defines different rules for different segments of the input domain. This approach offers greater flexibility in capturing potential patterns which might not be readily apparent. This approach requires analyzing potential relationships between the terms across different sections of the sequence. This might involve expressing the sequence as a series of equations or rules applied in distinct sections.
Method 6: The Importance of Context and Additional Information
The puzzle's solvability heavily relies on the context or any missing information. The sequence "x 2 2x 48 0" could be part of a larger problem, a coded message, or a step in a more extensive process. Without further context, definitively solving this requires making assumptions that may not reflect the intended solution.
Developing Critical Thinking Skills:
Problems like this highlight the value of developing critical thinking skills. The ability to systematically analyze, break down a problem, and explore various potential solutions is invaluable in numerous aspects of life. This puzzle illustrates several important aspects of problem-solving:
-
Systematic Approach: The importance of starting with basic methods and systematically progressing towards more complex techniques.
-
Flexibility: The need to adapt our approach as we gain more insights into the problem.
-
Pattern Recognition: The crucial role of identifying patterns, whether simple or complex, in solving mathematical puzzles.
-
Importance of Context: The significance of considering the context in which the problem arises.
Conclusion:
The sequence "x 2 2x 48 0" presents a challenging puzzle that requires a blend of mathematical knowledge and logical reasoning. While definitive solutions without further context are limited, the exploration of various methods and the insights gained from each approach are invaluable. This exercise serves as a strong testament to the importance of systematic thinking, analytical skills, and the ability to adapt our problem-solving approach as we gain new information. This type of puzzle strengthens cognitive skills that are highly valuable in both academic and professional pursuits. The process of tackling this seemingly simple puzzle offers a microcosm of the larger challenges we encounter in a world requiring critical thinking and adaptable problem-solving strategies. Without additional context or constraints, a unique solution is unlikely. The exercise underscores the significance of thorough analysis, systematic trial and error, and the value of understanding the limitations of available information in problem-solving.
Latest Posts
Latest Posts
-
5 X 20 7x 30
Sep 22, 2025
-
40 Yard Dash To Mph
Sep 22, 2025
-
Missing Angles In Triangles Worksheet
Sep 22, 2025
-
How Long Is 90 Monutes
Sep 22, 2025
-
Opponents Of Hamiltons Economic Plan
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about X 2 2x 48 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.