X 2 2x 8 0
gasmanvison
Sep 15, 2025 · 5 min read
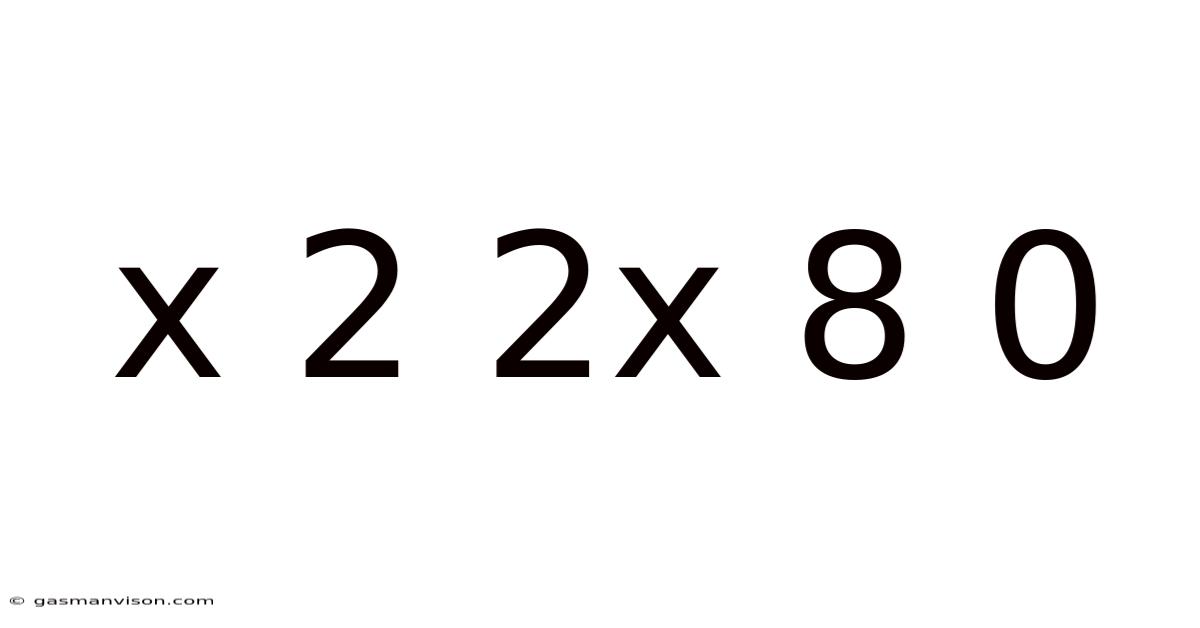
Table of Contents
Decoding the Mystery: x 2 2x 8 0 – A Mathematical Exploration
This seemingly simple sequence, "x 2 2x 8 0," presents a fascinating puzzle that delves into the world of algebra and equation solving. At first glance, it might appear cryptic, but with a methodical approach, we can unlock its secrets, exploring various mathematical concepts along the way. This article will dissect this sequence, providing a comprehensive understanding for both beginners and those seeking a deeper dive into mathematical problem-solving techniques.
What We'll Cover:
- Understanding the Nature of the Sequence
- Identifying the Equation: From Sequence to Algebraic Representation
- Solving the Equation: Multiple Approaches and Strategies
- Verification and Interpretation of Solutions
- Expanding the Scope: Exploring Related Concepts and Applications
Understanding the Nature of the Sequence:
The sequence "x 2 2x 8 0" isn't just a random arrangement of symbols; it hints at a mathematical relationship. The presence of "x" indicates a variable, a placeholder for an unknown value. The other elements—numbers and operators—suggest an algebraic equation. The ultimate goal is to find the value(s) of "x" that make the equation true. Understanding this fundamental aspect is crucial to successfully tackling the problem. This sequence likely represents a quadratic equation, a common type of equation in algebra that involves a variable raised to the power of two.
Identifying the Equation: From Sequence to Algebraic Representation:
The key is to translate the sequence into a proper algebraic equation. The sequence suggests a quadratic equation of the form: ax² + bx + c = 0, where 'a', 'b', and 'c' are coefficients. In our case, the sequence can be interpreted as:
x² + 2x + 8 = 0
This representation is vital because it allows us to apply various mathematical techniques designed to solve quadratic equations. This seemingly simple step forms the foundation of our problem-solving journey. The transition from a numerical sequence to a precise algebraic representation is a critical skill in mathematical problem-solving.
Solving the Equation: Multiple Approaches and Strategies:
Several methods exist for solving quadratic equations. Let's explore three common strategies:
-
Factoring: This involves expressing the quadratic equation as a product of two linear factors. Unfortunately, the equation x² + 2x + 8 = 0 doesn't easily factor using simple integers. We'd need to find two numbers that add up to 2 and multiply to 8, and no such integer pair exists. This leads us to other methods.
-
Quadratic Formula: This powerful formula provides a direct solution for any quadratic equation of the form ax² + bx + c = 0:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our equation (a = 1, b = 2, c = 8), we get:
x = [-2 ± √(2² - 4 * 1 * 8)] / 2 * 1 x = [-2 ± √(4 - 32)] / 2 x = [-2 ± √(-28)] / 2
Notice the appearance of the square root of a negative number (√-28). This indicates that the solutions are complex numbers, involving the imaginary unit "i," where i² = -1. We can simplify this further:
x = [-2 ± √(28)i] / 2 x = [-2 ± 2√(7)i] / 2 x = -1 ± √(7)i
Therefore, the solutions are x = -1 + √7i and x = -1 - √7i. These are complex conjugate solutions, a common characteristic of quadratic equations with no real roots.
-
Completing the Square: This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. Let's illustrate:
x² + 2x + 8 = 0 x² + 2x = -8 x² + 2x + 1 = -8 + 1 (Adding 1 to both sides to complete the square) (x + 1)² = -7 x + 1 = ±√(-7) x = -1 ± √7i
This method confirms the same complex solutions we obtained using the quadratic formula.
Verification and Interpretation of Solutions:
It's crucial to verify our solutions. Substituting x = -1 + √7i and x = -1 - √7i back into the original equation x² + 2x + 8 = 0 will confirm that they satisfy the equation. This verification step is essential to ensure the accuracy of our calculations. The fact that the solutions are complex numbers means that there are no real-number solutions to the given equation; the parabola represented by the equation doesn't intersect the x-axis.
Expanding the Scope: Exploring Related Concepts and Applications:
Understanding this simple equation opens doors to exploring more complex mathematical concepts:
-
Complex Numbers: The solutions highlight the importance of complex numbers in mathematics. These numbers extend the real number system to include imaginary units, crucial for various fields like electrical engineering, quantum mechanics, and signal processing.
-
Quadratic Equations and their Graphs: The equation represents a parabola. The absence of real solutions indicates that the parabola doesn't intersect the x-axis. Understanding the relationship between quadratic equations and their graphical representations is fundamental to algebra and calculus.
-
Discriminant: The expression b² - 4ac (inside the square root in the quadratic formula) is known as the discriminant. Its value determines the nature of the solutions:
- If b² - 4ac > 0, there are two distinct real solutions.
- If b² - 4ac = 0, there is one real solution (a repeated root).
- If b² - 4ac < 0, there are two complex conjugate solutions (as in our case).
-
Applications in Real-World Problems: While this specific equation might not directly model a real-world scenario, quadratic equations are fundamental to modeling various phenomena, including projectile motion, the trajectory of a ball, the shape of a satellite dish, and many more.
This comprehensive exploration of the sequence "x 2 2x 8 0" reveals far more than just a simple mathematical problem. It unveils the interconnectedness of various algebraic concepts, the power of different solving techniques, and the significance of complex numbers in mathematics and beyond. The seemingly simple puzzle serves as a stepping stone to a deeper understanding of algebra and its wide-ranging applications. By understanding this seemingly simple sequence, we've embarked on a journey that reveals the beauty and elegance of mathematical problem-solving. The exploration continues, and with each solved equation, our understanding of the mathematical world expands.
Latest Posts
Latest Posts
-
What Is 40 Of 10
Sep 15, 2025
-
1 1 2 Cup To Oz
Sep 15, 2025
-
300 Ml To Fl Oz
Sep 15, 2025
-
How To Calculate Class Width
Sep 15, 2025
-
The Proud Family Blue Sisters
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 2 2x 8 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.