X 2 2x 9 0
gasmanvison
Sep 22, 2025 · 5 min read
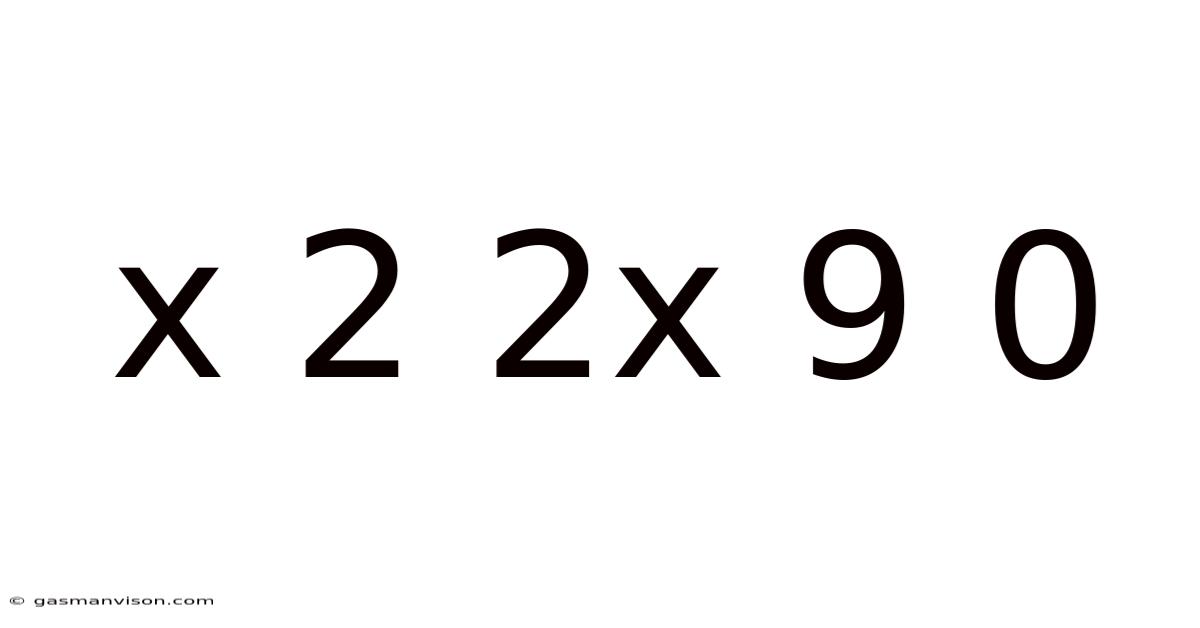
Table of Contents
Deconstructing the Enigma: Exploring the Mathematical and Symbolic Possibilities of "x 2 2x 9 0"
This seemingly simple string of characters, "x 2 2x 9 0," holds a wealth of potential interpretations, depending on the context. At first glance, it appears to represent a quadratic equation, a fundamental concept in algebra. However, delving deeper, we can uncover symbolic meanings and explore its application beyond pure mathematics. This article will dissect the various layers of meaning inherent within this seemingly simple sequence, examining its mathematical properties, potential symbolic interpretations, and practical applications.
Meta Description: Uncover the multifaceted meanings of "x 2 2x 9 0," from its algebraic representation as a quadratic equation to potential symbolic interpretations and real-world applications. Learn how to solve the equation and explore its significance beyond mathematics.
I. The Mathematical Heart: Solving the Quadratic Equation
The most straightforward interpretation of "x 2 2x 9 0" is as a quadratic equation. In standard form, it is written as:
x² + 2x - 9 = 0
This equation represents a parabola, a U-shaped curve, when graphed on a Cartesian coordinate system. Solving this equation means finding the values of 'x' that make the equation true. Several methods can be used:
A. Factoring: This method involves finding two binomials that, when multiplied, result in the original quadratic equation. Unfortunately, this equation doesn't factor neatly using integers.
B. Quadratic Formula: A more general and reliable method is the quadratic formula:
x = [-b ± √(b² - 4ac)] / 2a
Where 'a', 'b', and 'c' are the coefficients of the quadratic equation (ax² + bx + c = 0). In our case, a = 1, b = 2, and c = -9. Substituting these values into the formula gives:
x = [-2 ± √(2² - 4 * 1 * -9)] / (2 * 1) x = [-2 ± √(4 + 36)] / 2 x = [-2 ± √40] / 2 x = [-2 ± 2√10] / 2 x = -1 ± √10
Therefore, the two solutions to the equation are approximately x ≈ 2.162 and x ≈ -4.162.
C. Completing the Square: This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. While effective, it's slightly more complex than the quadratic formula for this particular equation.
These solutions represent the x-intercepts of the parabola, the points where the curve intersects the x-axis. Understanding these solutions is crucial for any further analysis or application of the equation.
II. Beyond the Numbers: Symbolic and Abstract Interpretations
While the mathematical solution is clear, "x 2 2x 9 0" can also hold symbolic weight depending on the context. The 'x' itself could represent an unknown variable or an abstract concept. The numbers could have further significance.
-
'x' as an Unknown: In a broader sense, 'x' can represent an unknown factor, a missing piece of information, or a challenge to be solved in any field, not just mathematics. The equation then becomes a metaphor for the process of uncovering the truth or finding a solution to a complex problem.
-
Numerical Symbolism: The specific numbers (2, 2, 9, 0) might hold symbolic meaning within certain cultural or religious contexts. Nine, for instance, often represents completion or wholeness in some belief systems. The repeated '2' could suggest duality or balance. The '0' could signify a starting point or a state of nothingness. However, without a specific context, such interpretations remain speculative.
-
The Equation as a Metaphor: The entire equation itself could symbolize the challenges and complexities of life. The process of solving the equation mirrors the struggle to overcome obstacles and find solutions to life's problems. The solutions (the x-intercepts) represent the potential outcomes or resolutions.
III. Practical Applications in Different Fields
The principles underlying this seemingly simple quadratic equation have wide-ranging applications across various disciplines:
-
Physics: Quadratic equations frequently appear in physics, especially in kinematics (the study of motion). Calculating projectile trajectories, determining the velocity of an object under constant acceleration, and modeling oscillations often involve solving quadratic equations.
-
Engineering: Engineers use quadratic equations to design structures, analyze stresses and strains, and model various systems. For example, calculating the optimal dimensions of a bridge or determining the stability of a building might involve solving quadratic equations.
-
Economics: Quadratic functions are used in economics to model supply and demand curves, optimize production levels, and analyze market equilibrium. Understanding quadratic equations is therefore vital for economic modeling and forecasting.
-
Computer Science: Solving quadratic equations is essential in various computer science algorithms and applications, including optimization problems, graphics rendering, and computer simulations.
IV. Expanding the Scope: Variations and Extensions
The expression "x 2 2x 9 0" can be expanded upon and altered to explore more complex mathematical concepts. For example:
-
Inequalities: Instead of an equation, we could consider inequalities like x² + 2x - 9 > 0 or x² + 2x - 9 < 0. Solving these inequalities would involve finding the ranges of x-values that satisfy the conditions. This would involve analyzing the parabola's position relative to the x-axis.
-
Complex Numbers: If the discriminant (b² - 4ac) were negative, the quadratic equation would have complex solutions involving the imaginary unit 'i' (√-1). This would open up a new dimension of mathematical analysis.
-
Higher-Order Polynomials: The equation could be extended to include higher-order terms, creating cubic, quartic, or even higher-degree polynomials. Solving these would be more complex but would reveal richer mathematical structures.
-
Multivariate Equations: The equation could be extended to involve multiple variables, leading to systems of equations or multivariable functions. This opens the door to more advanced mathematical techniques like linear algebra and multivariable calculus.
V. Conclusion: A Simple Equation, Profound Implications
The seemingly simple expression "x 2 2x 9 0" serves as a microcosm of the power and versatility of mathematics. Its initial interpretation as a quadratic equation provides a foundation for understanding various mathematical concepts. However, by exploring its symbolic interpretations and potential applications across diverse fields, we uncover a much deeper and richer meaning. This simple sequence transcends its mathematical roots, becoming a metaphor for problem-solving, the search for solutions, and the inherent complexities within various systems. The exploration of this equation highlights the interconnectedness of mathematics and the real world, demonstrating the profound implications even within the simplest of mathematical expressions. Further investigation into its variations and extensions reveals a vast landscape of mathematical possibilities, highlighting the continuous evolution and expansion of mathematical knowledge.
Latest Posts
Latest Posts
-
97 7 F To C
Sep 22, 2025
-
Electron Pair Geometry Of Pf3
Sep 22, 2025
-
Order Of Three Compartment Sink
Sep 22, 2025
-
African With Chad Identified Map
Sep 22, 2025
-
How To Calculate Z Score
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about X 2 2x 9 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.