X 2 3x 18 0
gasmanvison
Sep 23, 2025 · 5 min read
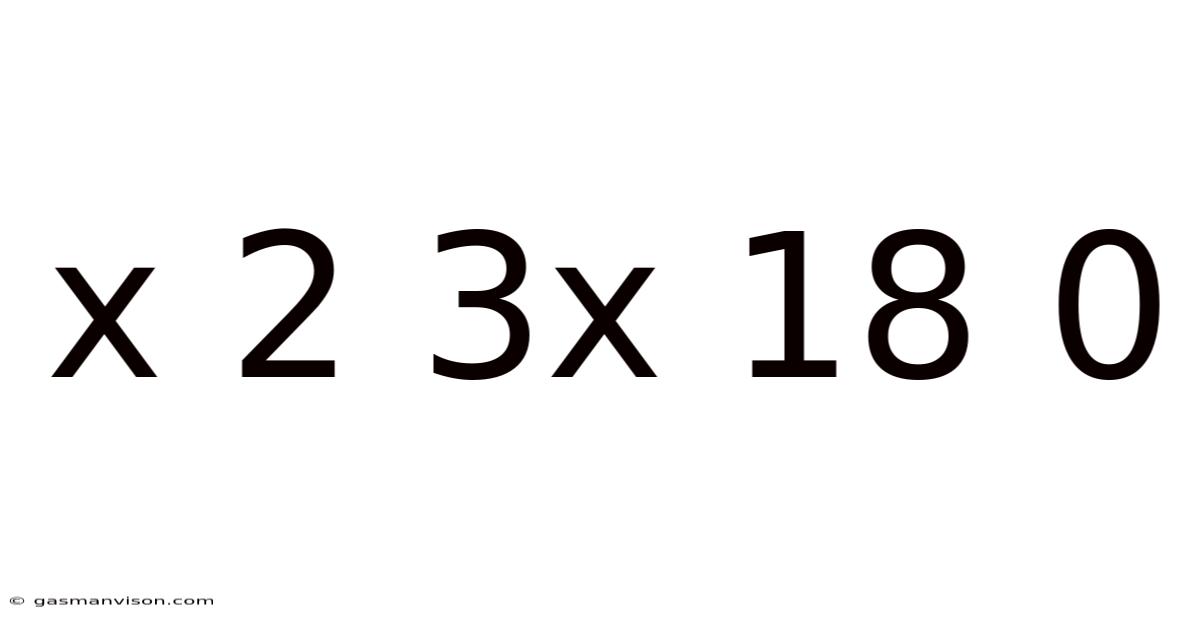
Table of Contents
Decoding the Sequence: x 2 3x 18 0 – A Deep Dive into Mathematical Patterns and Problem-Solving
This article explores the intriguing mathematical sequence "x 2 3x 18 0," examining potential interpretations, underlying patterns, and different approaches to solving for the unknown variable 'x'. We will delve into various mathematical concepts, including algebraic manipulation, quadratic equations, and logical deduction, to uncover the solutions and understand the principles behind them. This exploration will cater to readers with a range of mathematical backgrounds, from beginners seeking to improve their problem-solving skills to more advanced students interested in exploring the nuances of mathematical reasoning.
Meta Description: Unravel the mystery of the mathematical sequence "x 2 3x 18 0." This article provides a comprehensive guide to solving for 'x', exploring various mathematical concepts and techniques, suitable for all levels of mathematical proficiency.
Understanding the Sequence and Potential Interpretations
The sequence "x 2 3x 18 0" presents a seemingly simple yet intriguing puzzle. The presence of "x" immediately indicates that we're dealing with an algebraic equation, not simply a numerical sequence. However, the lack of explicit operators between the elements (e.g., "+" or "-") requires careful consideration of possible interpretations.
One of the most likely interpretations is that the sequence represents a quadratic equation. The presence of the terms "x" and "3x" strongly suggests this. Therefore, we can rewrite the sequence as a standard quadratic equation:
x² + 3x - 18 = 0
This interpretation forms the basis for our primary exploration. However, it's important to acknowledge that other interpretations might exist depending on the context or additional information provided. For example, it could potentially represent a sequence of operations with implicit operators, although this scenario is less probable given the common mathematical conventions.
Solving the Quadratic Equation: Factoring Method
The most straightforward method for solving the quadratic equation x² + 3x - 18 = 0 is factoring. Factoring involves expressing the quadratic expression as a product of two simpler expressions. We look for two numbers that add up to 3 (the coefficient of 'x') and multiply to -18 (the constant term).
These numbers are 6 and -3. Therefore, we can factor the quadratic equation as follows:
(x + 6)(x - 3) = 0
This equation is satisfied if either (x + 6) = 0 or (x - 3) = 0. Solving these individual equations gives us the two solutions for 'x':
- x = -6
- x = 3
Solving the Quadratic Equation: Quadratic Formula
Another widely used method for solving quadratic equations is the quadratic formula. This formula provides a general solution for any quadratic equation of the form ax² + bx + c = 0, where 'a', 'b', and 'c' are constants. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
In our case, a = 1, b = 3, and c = -18. Substituting these values into the quadratic formula gives:
x = [-3 ± √(3² - 4 * 1 * -18)] / (2 * 1) x = [-3 ± √(9 + 72)] / 2 x = [-3 ± √81] / 2 x = [-3 ± 9] / 2
This gives us the same two solutions as before:
- x = (-3 + 9) / 2 = 3
- x = (-3 - 9) / 2 = -6
Graphical Representation and Interpretation
Visualizing the quadratic equation graphically provides further insight. The equation x² + 3x - 18 = 0 represents a parabola. The solutions for 'x' represent the x-intercepts of the parabola, the points where the parabola intersects the x-axis (where y = 0). Plotting the parabola reveals these intercepts clearly at x = 3 and x = -6, confirming our algebraic solutions. This graphical representation helps in understanding the relationship between the equation and its solutions in a visual context, reinforcing the concept of roots and intercepts in quadratic equations.
Exploring Alternative Interpretations (Less Likely Scenarios)
While the quadratic equation interpretation is the most probable, it’s crucial to consider alternative, albeit less likely, possibilities. For instance, the sequence could represent a series of operations with implied operators. However, without further context or information, such interpretations remain speculative. One could potentially imagine scenarios involving implied multiplication or other operations, but these interpretations would be highly context-dependent and lack the mathematical consistency of the quadratic equation interpretation.
Applications and Further Exploration
The ability to solve quadratic equations like x² + 3x - 18 = 0 is fundamental to numerous areas within mathematics, science, and engineering. Such equations frequently appear in:
- Physics: Modeling projectile motion, calculating the trajectory of objects under gravity.
- Engineering: Designing structures, analyzing stress and strain in materials.
- Economics: Analyzing economic growth models, predicting market trends.
- Computer Science: Developing algorithms, solving optimization problems.
Further exploration of quadratic equations could involve investigating the discriminant (b² - 4ac), which determines the nature of the roots (real and distinct, real and equal, or complex). Understanding the discriminant helps in predicting the number and type of solutions a quadratic equation will have before attempting to solve it. Advanced topics like complex numbers may also be relevant when dealing with quadratic equations that have no real roots.
Conclusion: The Importance of Mathematical Reasoning
The seemingly simple sequence "x 2 3x 18 0" has led us on a journey through various mathematical concepts and problem-solving techniques. The key takeaway is that careful observation, logical deduction, and a systematic approach are crucial to unraveling mathematical puzzles. The ability to interpret mathematical notations, identify the appropriate method of solution, and verify the results is essential for success in mathematics and its numerous applications. By understanding the principles behind solving quadratic equations, we build a strong foundation for tackling more complex mathematical problems and developing critical thinking skills applicable in various fields. While the quadratic equation interpretation provided the most plausible and comprehensive solution, acknowledging the possibility of alternative interpretations highlights the importance of context and critical thinking when approaching any mathematical problem. The exploration of this sequence exemplifies the multifaceted nature of mathematics and its power in solving real-world problems.
Latest Posts
Latest Posts
-
Moons Over Myh Hammy Pun
Sep 23, 2025
-
Ser Vs Estar Worksheet Answers
Sep 23, 2025
-
Beryllium And Nitrogen Ionic Charges
Sep 23, 2025
-
How Did Aristotle Classify Organisms
Sep 23, 2025
-
Eukaryotes Vs Prokaryotes Venn Diagram
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about X 2 3x 18 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.