X 2 3x 7 0
gasmanvison
Sep 17, 2025 · 5 min read
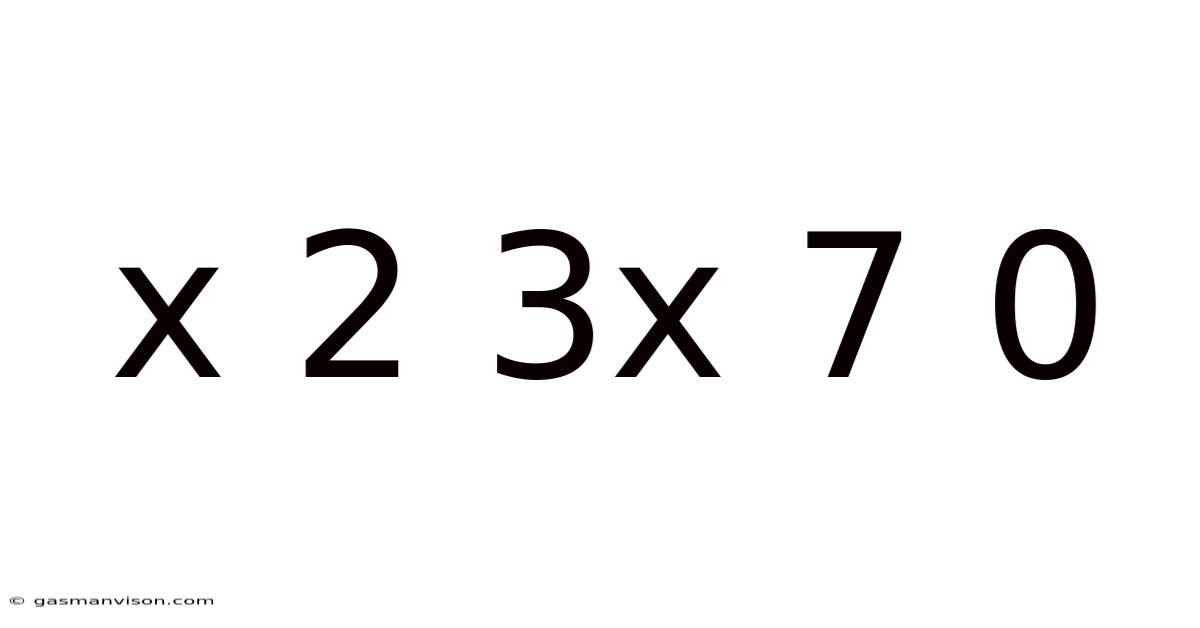
Table of Contents
Decoding the Sequence: Exploring the Mathematical and Algorithmic Possibilities of "x 2 3x 7 0"
This seemingly simple sequence, "x 2 3x 7 0," presents a fascinating puzzle that can be approached from various mathematical and algorithmic perspectives. At first glance, it appears arbitrary. However, a deeper dive reveals potential patterns, relationships, and interpretations, opening doors to a rich exploration of mathematical reasoning and computational thinking. This article delves into multiple possibilities, examining potential mathematical structures, exploring algorithmic approaches to generate similar sequences, and considering the broader implications of such investigations.
What makes this sequence intriguing? The absence of clear operators initially makes the sequence ambiguous. Is it a simple arithmetic progression? A geometric progression? Or perhaps something more complex, involving hidden operations or a completely different underlying logic? The very ambiguity compels us to investigate different possibilities, fostering a deeper understanding of mathematical concepts and problem-solving strategies. The presence of "x," a common algebraic variable, further adds to the complexity and suggests a potential connection to equations or algebraic expressions.
1. Exploring Arithmetic and Geometric Progressions:
The most straightforward approach is to examine whether the sequence follows a standard arithmetic or geometric progression. Let's analyze this:
-
Arithmetic Progression: An arithmetic progression has a constant difference between consecutive terms. In this case, the differences are not consistent: 2-x, 3x-2, 7-3x, and 0-7. There's no obvious constant difference.
-
Geometric Progression: A geometric progression has a constant ratio between consecutive terms. Again, applying this to the sequence doesn't reveal a consistent ratio.
The absence of a simple arithmetic or geometric progression indicates that a more sophisticated approach is required.
2. Algebraic Interpretations and Equation Solving:
The presence of "x" strongly suggests that the sequence is related to an underlying algebraic equation or system of equations. We can try to formulate potential relationships:
-
Possible Equation 1: Let's assume the sequence represents the roots of a polynomial equation. However, finding a polynomial equation with these roots (x, 2, 3x, 7, 0) is challenging, and the solution might not be unique.
-
Possible Equation 2: Another approach could be to consider pairs of consecutive terms as related through an equation. For example, we could explore relationships like:
- 2 = f(x)
- 3x = g(2)
- 7 = h(3x)
- 0 = i(7)
where f, g, h, and i represent some mathematical functions. This approach opens up a vast number of possibilities, requiring further constraints or information to narrow down the potential solutions.
-
System of Equations: A system of equations might be required to capture the relationships between the terms, particularly if we consider the 'x' as a variable that influences the sequence’s progression. For example, we could attempt to construct a system of equations where each term is a function of 'x' and the previous terms. Solving such a system would require sophisticated techniques and might lead to multiple solutions.
3. Algorithmic Generation of Similar Sequences:
Rather than seeking a specific mathematical formula, we can approach this from an algorithmic perspective. We could design an algorithm that generates sequences with similar characteristics:
-
Recursive Algorithm: A recursive algorithm could be created to generate sequences where each term is a function of previous terms and the variable 'x'. The function could incorporate parameters that allow for varying the sequence's behavior. This would create a family of sequences exhibiting similar properties to the original sequence.
-
Iterative Algorithm: An iterative algorithm would achieve the same outcome, but without the use of recursive function calls. This approach would involve defining a set of rules that determine how each element in the sequence is calculated based on its position and the value of 'x'.
-
Random Sequence Generation: We could create an algorithm that generates pseudo-random sequences containing a mix of numbers and variables, incorporating constraints similar to the original sequence (e.g., presence of 'x', varying numerical values). This approach could help us explore a wider space of possibilities and observe potential emerging patterns. Such patterns could then suggest further refinement of mathematical models to describe the structure.
4. Exploring the Role of "x":
The variable 'x' is a crucial element. It could represent:
-
A Parameter: 'x' could be a parameter controlling the sequence's generation, much like parameters in algorithmic approaches. Different values of 'x' would yield different sequences.
-
An Unknown: 'x' could be an unknown variable to be solved for within a larger mathematical context. Without further information or constraints, determining the value of 'x' remains impossible.
-
A Placeholder: 'x' could be a simple placeholder, with its actual value unimportant in understanding the fundamental structure of the sequence.
5. Implications and Further Exploration:
The exploration of this sequence highlights the importance of:
-
Multiple Perspectives: Mathematical problems can often be approached from various angles (algebraic, algorithmic, statistical), leading to deeper insights.
-
Ambiguity and Creativity: Ambiguous problems, like this sequence, encourage creative problem-solving and the development of innovative approaches.
-
Computational Thinking: Designing algorithms to generate similar sequences demonstrates the power of computational thinking in tackling mathematical challenges.
6. Advanced Mathematical Concepts and Future Directions:
The analysis could be extended to involve more advanced mathematical concepts:
-
Abstract Algebra: Exploring group theory or other abstract algebra structures could provide a framework for understanding the underlying relationships between the terms.
-
Number Theory: If the sequence were to be modified to contain only integers, exploring concepts from number theory might provide further insights.
-
Chaos Theory: In the context of recursive algorithms, investigating the sensitivity to initial conditions could reveal interesting dynamics and potentially chaotic behavior.
Conclusion:
The sequence "x 2 3x 7 0" presents a rich challenge for mathematical and computational exploration. While a definitive, single solution remains elusive without further context or constraints, the process of investigating its potential interpretations unveils valuable insights into mathematical reasoning, algorithmic design, and the power of approaching problems from multiple perspectives. The ambiguity of the sequence stimulates creative problem-solving and highlights the beauty of mathematics in its capacity to present seemingly simple puzzles with a surprising depth of complexity. Further research involving advanced mathematical concepts could potentially unlock deeper understandings and reveal more profound connections within this seemingly simple sequence.
Latest Posts
Latest Posts
-
How Many Is 120 Inches
Sep 17, 2025
-
23 Repeating As A Fraction
Sep 17, 2025
-
What Is 40 Of 20 00
Sep 17, 2025
-
Which Structure Is Highlighted Ovary
Sep 17, 2025
-
Articles On Teens Going Pro
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about X 2 3x 7 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.