X 2 5x 2 0
gasmanvison
Sep 15, 2025 · 5 min read
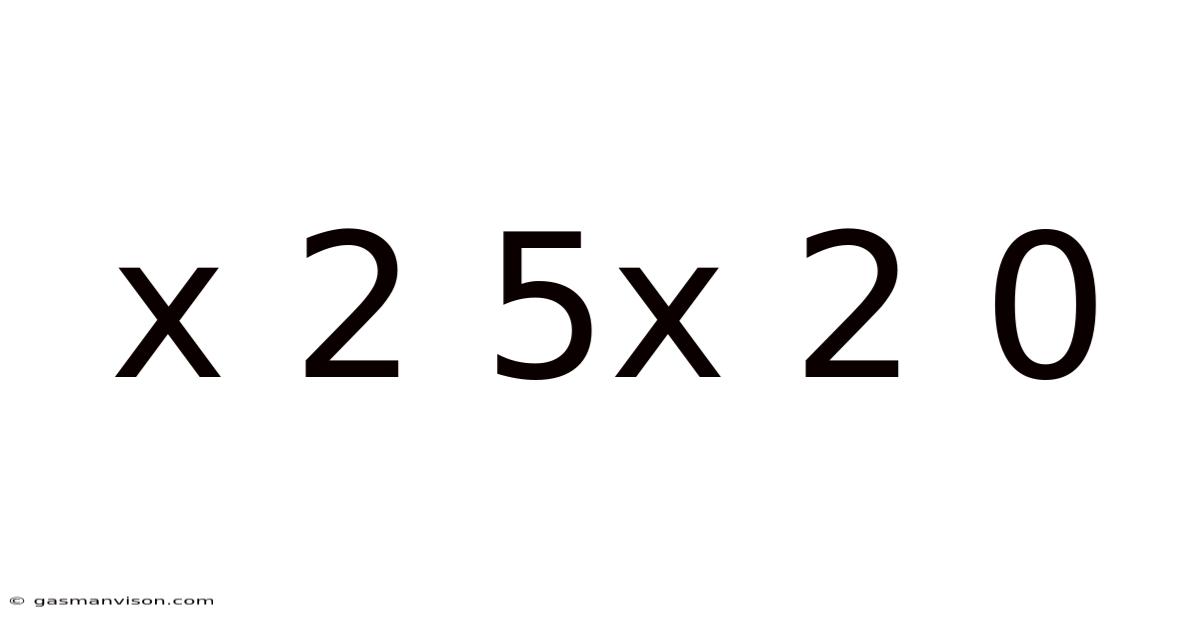
Table of Contents
Deconstructing x² + 5x + 2 = 0: A Deep Dive into Quadratic Equations
This article delves into the seemingly simple quadratic equation x² + 5x + 2 = 0, exploring its various solutions, applications, and the broader context of quadratic equations within mathematics. Understanding this seemingly simple equation unlocks a world of mathematical concepts applicable across diverse fields, from physics and engineering to finance and computer science. We will dissect the equation using multiple methods, examining its roots, discriminant, and graphical representation. This comprehensive guide aims to be accessible to both beginners and those seeking a deeper understanding of quadratic equations.
What is a Quadratic Equation?
A quadratic equation is a second-degree polynomial equation, meaning the highest power of the variable (in this case, x) is 2. The general form is ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0. Our specific equation, x² + 5x + 2 = 0, fits this form with a = 1, b = 5, and c = 2. The solutions to this equation, also known as roots or zeros, represent the x-values where the equation equals zero. These roots can be real or complex numbers.
Solving x² + 5x + 2 = 0 using the Quadratic Formula
The quadratic formula provides a universal method for solving any quadratic equation. It's derived from completing the square and offers a straightforward approach to finding the roots. The formula is:
x = (-b ± √(b² - 4ac)) / 2a
Substituting the values from our equation (a = 1, b = 5, c = 2), we get:
x = (-5 ± √(5² - 4 * 1 * 2)) / (2 * 1) x = (-5 ± √(25 - 8)) / 2 x = (-5 ± √17) / 2
This gives us two distinct real roots:
x₁ = (-5 + √17) / 2 ≈ -0.438 x₂ = (-5 - √17) / 2 ≈ -4.562
Solving x² + 5x + 2 = 0 by Completing the Square
Completing the square is another powerful method for solving quadratic equations. This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored.
-
Move the constant term: Subtract 2 from both sides: x² + 5x = -2
-
Complete the square: Take half of the coefficient of x (5/2), square it (25/4), and add it to both sides: x² + 5x + 25/4 = -2 + 25/4
-
Factor the perfect square trinomial: (x + 5/2)² = 17/4
-
Solve for x: Take the square root of both sides: x + 5/2 = ±√(17/4) => x = -5/2 ± √17/2
This yields the same roots as the quadratic formula: x₁ = (-5 + √17) / 2 and x₂ = (-5 - √17) / 2.
The Discriminant and the Nature of Roots
The discriminant, represented by Δ (delta), is the expression inside the square root in the quadratic formula (b² - 4ac). The discriminant determines the nature of the roots:
- Δ > 0: Two distinct real roots (as in our case)
- Δ = 0: One real root (a repeated root)
- Δ < 0: Two complex conjugate roots
In our equation, Δ = 5² - 4 * 1 * 2 = 17 > 0, confirming the existence of two distinct real roots.
Graphical Representation of x² + 5x + 2 = 0
The graph of the quadratic equation y = x² + 5x + 2 is a parabola. The roots of the equation are the x-intercepts of the parabola—the points where the parabola intersects the x-axis (where y = 0). Graphing this parabola visually confirms the two real roots we calculated earlier, approximately -0.438 and -4.562. The parabola opens upwards because the coefficient of x² (a) is positive. The vertex of the parabola, representing the minimum value of the function, can be found using the formula x = -b/2a, which gives x = -5/2 = -2.5. Substituting this back into the equation gives the y-coordinate of the vertex.
Applications of Quadratic Equations
Quadratic equations have wide-ranging applications in various fields:
- Physics: Calculating projectile motion, determining the trajectory of objects under gravity.
- Engineering: Designing structures, analyzing stress and strain in materials, modeling electrical circuits.
- Finance: Calculating compound interest, determining break-even points in business models.
- Computer Graphics: Creating curves and shapes, modeling three-dimensional objects.
- Optimization problems: Finding maximum or minimum values of functions.
Beyond the Basics: Exploring Related Concepts
Understanding x² + 5x + 2 = 0 provides a foundation for exploring more advanced concepts:
- Polynomial Equations: Quadratic equations are a subset of polynomial equations. Higher-degree polynomial equations can be solved using numerical methods or factorization techniques.
- Complex Numbers: When the discriminant is negative, the roots are complex numbers, involving the imaginary unit 'i' (√-1).
- Calculus: Quadratic equations play a role in optimization problems, finding derivatives and integrals.
- Linear Algebra: Quadratic forms are used in various linear algebra applications, including matrix diagonalization.
Approximating Roots using Numerical Methods
While the quadratic formula provides an exact solution, numerical methods offer approximations, especially useful for higher-degree polynomials or equations without closed-form solutions. Methods like the Newton-Raphson method iteratively refine an initial guess to approach the root with increasing accuracy.
Conclusion
The seemingly simple equation x² + 5x + 2 = 0 opens doors to a rich understanding of quadratic equations and their applications. By mastering the various methods of solving these equations—the quadratic formula, completing the square, and graphical analysis—we gain a deeper appreciation for the fundamental principles of algebra and their relevance to a multitude of disciplines. Furthermore, exploring related concepts such as the discriminant and numerical methods expands our mathematical toolkit and prepares us to tackle more complex problems in the future. The journey from understanding this basic equation to grasping its broader implications showcases the power and elegance of mathematics. It's a testament to how seemingly simple mathematical constructs can form the foundation for solving intricate real-world problems.
Latest Posts
Latest Posts
-
Meaning Of Soft Shoulder Sign
Sep 15, 2025
-
Speed Limit For Blind Intersection
Sep 15, 2025
-
How Many Oz In 2l
Sep 15, 2025
-
5 8 Cup To 1 4 Cup
Sep 15, 2025
-
Degrees Of Lewdity Love Interests
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 2 5x 2 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.