X 2 5x 3 0
gasmanvison
Sep 14, 2025 · 5 min read
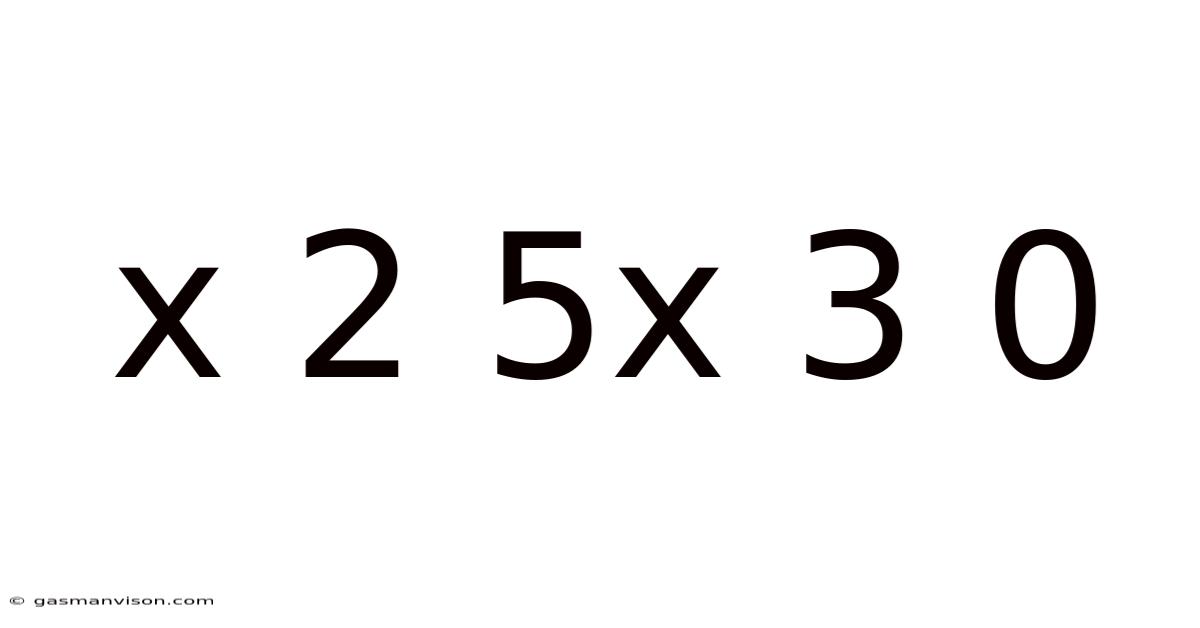
Table of Contents
Deconstructing the Expression: x² + 5x + 3 = 0
This article delves into the intricacies of the quadratic equation x² + 5x + 3 = 0, exploring various methods for solving it and highlighting its applications in mathematics and beyond. We will cover the quadratic formula, factoring techniques (where applicable), completing the square, and discuss the nature of its roots. Understanding this seemingly simple equation unlocks a deeper comprehension of fundamental algebraic concepts and their practical uses. This comprehensive guide is designed for students, educators, and anyone seeking a robust understanding of quadratic equations.
Introduction: Understanding Quadratic Equations
A quadratic equation is a second-degree polynomial equation of the general form ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Our specific focus, x² + 5x + 3 = 0, fits this mold with a = 1, b = 5, and c = 3. Solving quadratic equations involves finding the values of 'x' that satisfy the equation, meaning the values that make the equation true. These values are known as the roots or solutions of the equation. The nature of these roots (real or complex, distinct or repeated) depends on the discriminant (b² - 4ac), a value we will explore further.
Method 1: The Quadratic Formula – A Universal Approach
The quadratic formula provides a direct and reliable method for solving any quadratic equation, regardless of whether it's easily factorable. The formula is derived from completing the square (a method we'll examine later) and is expressed as:
x = [-b ± √(b² - 4ac)] / 2a
For our equation, x² + 5x + 3 = 0, we substitute a = 1, b = 5, and c = 3:
x = [-5 ± √(5² - 4 * 1 * 3)] / (2 * 1) x = [-5 ± √(25 - 12)] / 2 x = [-5 ± √13] / 2
This gives us two distinct real roots:
x₁ = (-5 + √13) / 2 ≈ -0.697 x₂ = (-5 - √13) / 2 ≈ -4.303
These are the approximate values; the exact solutions remain as expressed above. The quadratic formula guarantees a solution for all quadratic equations, making it a powerful tool in algebra.
Method 2: Attempting to Factor – A Simpler, But Not Always Possible, Method
Factoring involves expressing the quadratic equation as a product of two linear expressions. While not always feasible (as in this case), it's a valuable method when applicable because it provides a quicker solution. We look for two numbers that add up to 'b' (5) and multiply to 'c' (3). In this instance, there are no two integers that satisfy this condition. This indicates that our quadratic equation cannot be easily factored using integers. However, for equations that can be factored, this method is significantly faster than using the quadratic formula.
Method 3: Completing the Square – A Geometric and Algebraic Insight
Completing the square is a powerful technique that transforms the quadratic equation into a perfect square trinomial, making it easier to solve. The process involves manipulating the equation to create a perfect square on one side. Let's illustrate this for x² + 5x + 3 = 0:
-
Move the constant term: x² + 5x = -3
-
Find the value to complete the square: Take half of the coefficient of 'x' (5/2) and square it ((5/2)² = 25/4).
-
Add and subtract this value: x² + 5x + 25/4 - 25/4 = -3
-
Factor the perfect square trinomial: (x + 5/2)² - 25/4 = -3
-
Solve for x: (x + 5/2)² = -3 + 25/4 = 13/4
x + 5/2 = ±√(13/4)
x = -5/2 ± √13/2
This yields the same solutions as the quadratic formula, demonstrating the equivalence of the methods. Completing the square provides a deeper geometric understanding of quadratic equations, showing their connection to conic sections.
Understanding the Discriminant (b² - 4ac)
The discriminant, (b² - 4ac), plays a crucial role in determining the nature of the roots of a quadratic equation:
-
b² - 4ac > 0: The equation has two distinct real roots, as seen in our example (13 > 0). This means the parabola intersects the x-axis at two different points.
-
b² - 4ac = 0: The equation has one real root (a repeated root). The parabola touches the x-axis at exactly one point.
-
b² - 4ac < 0: The equation has two complex conjugate roots. The parabola does not intersect the x-axis.
In our case, the discriminant is 13, confirming the existence of two distinct real roots.
Applications of Quadratic Equations
Quadratic equations are not merely abstract mathematical concepts; they find widespread application in various fields:
-
Physics: Calculating projectile motion, determining the trajectory of objects under the influence of gravity. Understanding the time it takes for an object to reach a certain height or distance.
-
Engineering: Designing bridges, buildings, and other structures. Analyzing stress and strain on materials. Optimizing designs for strength and efficiency.
-
Economics: Modeling supply and demand curves, determining optimal production levels, and analyzing market equilibrium.
-
Computer Graphics: Creating curves and shapes for animations and games. Modeling realistic objects and environments.
-
Statistics: Analyzing data sets, performing regression analysis, and modeling relationships between variables.
Graphical Representation and Interpretation
The graph of a quadratic equation is a parabola. The roots of the equation represent the x-intercepts of the parabola – the points where the parabola intersects the x-axis. The parabola opens upwards if 'a' > 0 and downwards if 'a' < 0. Our equation, x² + 5x + 3 = 0, has a parabola that opens upwards (since a = 1 > 0) and intersects the x-axis at two points corresponding to our calculated roots. Visualizing the graph helps in understanding the nature and behavior of the roots.
Advanced Concepts and Extensions
The exploration of quadratic equations can extend to more advanced topics, such as:
-
Complex Numbers: Understanding how to deal with equations that have complex roots.
-
System of Quadratic Equations: Solving systems involving multiple quadratic equations.
-
Quadratic Inequalities: Determining the intervals where the quadratic expression is positive or negative.
-
Applications in Calculus: Using quadratic equations in optimization problems, finding maxima and minima of functions.
Conclusion: Mastering the Fundamentals
The quadratic equation x² + 5x + 3 = 0 serves as a fundamental building block in algebra and mathematics as a whole. Mastering its solution through various methods—the quadratic formula, completing the square (when applicable)—provides a solid foundation for tackling more complex mathematical problems. Understanding the discriminant and the graphical representation enhances comprehension and application in real-world scenarios. The breadth of its applications underscores its importance in diverse fields, solidifying its position as a cornerstone concept in mathematical education. Further exploration into related concepts will strengthen your mathematical skills and open doors to more advanced mathematical studies.
Latest Posts
Latest Posts
-
Why Do Organisms Do Mitosis
Sep 15, 2025
-
0 5 As A Mixed Number
Sep 15, 2025
-
Soft Shoulder Road Sign Meaning
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 2 5x 3 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.