X 2 5x 5 0
gasmanvison
Sep 08, 2025 · 5 min read
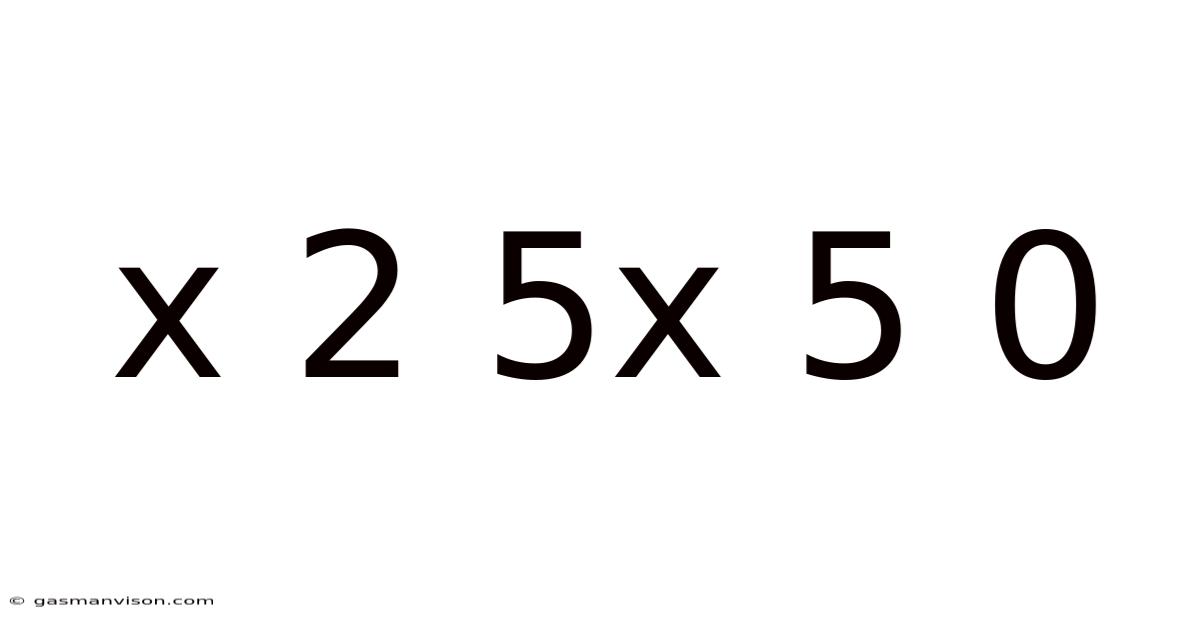
Table of Contents
Decoding the Enigma: x² + 5x + 5 = 0 and the World of Quadratic Equations
This article delves into the seemingly simple, yet surprisingly rich, quadratic equation x² + 5x + 5 = 0. We will explore its solution using various methods, analyze its properties, and connect it to broader mathematical concepts. This equation serves as a perfect microcosm to understand the wider world of quadratic equations, their applications, and their significance in mathematics and beyond. Understanding this seemingly simple equation opens doors to a deeper appreciation of algebra and its power in solving real-world problems.
What is a Quadratic Equation?
Before diving into the specifics of x² + 5x + 5 = 0, let's establish a foundational understanding. A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (in this case, 'x') is 2. The general form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0. Our equation, x² + 5x + 5 = 0, fits this form perfectly, with a = 1, b = 5, and c = 5.
Solving x² + 5x + 5 = 0: The Quadratic Formula
One of the most common and versatile methods for solving quadratic equations is the quadratic formula. This formula provides a direct solution for x, given the values of a, b, and c. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
Plugging in the values from our equation (a = 1, b = 5, c = 5), we get:
x = [-5 ± √(5² - 4 * 1 * 5)] / 2 * 1 x = [-5 ± √(25 - 20)] / 2 x = [-5 ± √5] / 2
This gives us two distinct solutions:
x₁ = (-5 + √5) / 2 ≈ -0.382 x₂ = (-5 - √5) / 2 ≈ -4.618
These are the exact solutions to the equation. The approximate values provide a more readily understandable numerical representation. These solutions represent the points where the parabola represented by the equation intersects the x-axis.
Solving x² + 5x + 5 = 0: Completing the Square
Another powerful method for solving quadratic equations is completing the square. This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored.
-
Move the constant term: Subtract 5 from both sides of the equation: x² + 5x = -5
-
Complete the square: To complete the square for x² + 5x, we take half of the coefficient of x (which is 5/2), square it ((5/2)² = 25/4), and add it to both sides:
x² + 5x + 25/4 = -5 + 25/4
- Factor the perfect square trinomial: The left side now factors as a perfect square:
(x + 5/2)² = 5/4
- Solve for x: Take the square root of both sides:
x + 5/2 = ±√(5/4) x = -5/2 ± √5/2
This simplifies to the same solutions we obtained using the quadratic formula:
x₁ = (-5 + √5) / 2 x₂ = (-5 - √5) / 2
Analyzing the Discriminant: b² - 4ac
The expression b² - 4ac, found within the quadratic formula, is known as the discriminant. It provides valuable information about the nature of the solutions to the quadratic equation:
- b² - 4ac > 0: The equation has two distinct real roots (as in our case).
- b² - 4ac = 0: The equation has one real root (a repeated root).
- b² - 4ac < 0: The equation has two complex roots (roots involving the imaginary unit 'i').
In our equation, b² - 4ac = 5² - 4 * 1 * 5 = 5 > 0, confirming the existence of two distinct real roots.
Graphical Representation and the Parabola
The equation x² + 5x + 5 = 0 represents a parabola. The parabola opens upwards (since the coefficient of x² is positive). The x-intercepts of the parabola are the solutions to the equation – the points where the parabola crosses the x-axis. The y-intercept is found by setting x = 0, giving y = 5. Understanding the parabola's characteristics provides a visual representation of the equation's solutions and behavior.
Applications of Quadratic Equations
Quadratic equations have extensive applications across various fields:
- Physics: Calculating projectile motion, determining the trajectory of objects under gravity.
- Engineering: Designing bridges, structures, and other engineering marvels.
- Economics: Modeling supply and demand curves, optimizing production levels.
- Computer Graphics: Creating curves and shapes in computer-aided design (CAD) software.
- Mathematics: Solving complex problems in calculus, algebra, and other mathematical branches.
The seemingly simple equation x² + 5x + 5 = 0 serves as a foundational building block for understanding and applying these more complex concepts.
Extending the Understanding: Complex Numbers
While our equation yielded real solutions, many quadratic equations have complex solutions. Complex numbers involve the imaginary unit 'i', where i² = -1. Understanding complex numbers is crucial for a complete grasp of quadratic equations and their applications in advanced mathematics and science.
The Power of Numerical Methods
For equations that are difficult or impossible to solve analytically (using algebraic methods), numerical methods offer powerful alternatives. These methods use iterative processes to approximate the solutions to a desired level of accuracy. Newton-Raphson method and other iterative techniques are often employed to find the roots of complex equations.
Conclusion: A Deeper Dive into Simplicity
The equation x² + 5x + 5 = 0, while seemingly simple, offers a rich tapestry of mathematical concepts and applications. Through the exploration of its solutions using different methods, the analysis of its discriminant, and the visualization of its graphical representation, we gain a deeper appreciation for the power and elegance of quadratic equations. This journey underscores the importance of fundamental mathematical principles and their far-reaching implications in various fields. From the simple elegance of the quadratic formula to the power of numerical methods, the exploration of this equation provides a solid foundation for further mathematical pursuits. The seemingly simple equation unlocks a world of possibilities, highlighting the beauty and practicality of mathematics in our world. Further study into the topic can reveal even more intricate details and applications of this fundamental concept, emphasizing its enduring relevance in modern mathematics and its applications.
Latest Posts
Latest Posts
-
Aortic Root Dilated Icd 10
Sep 09, 2025
-
10 To The Seventh Power
Sep 09, 2025
-
Nonexcludability Describes A Condition Where
Sep 09, 2025
-
Which Response Core Capability Involves
Sep 09, 2025
-
Is Xef4 Polar Or Nonpolar
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about X 2 5x 5 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.