X 2 8x 15 0
gasmanvison
Sep 20, 2025 · 5 min read
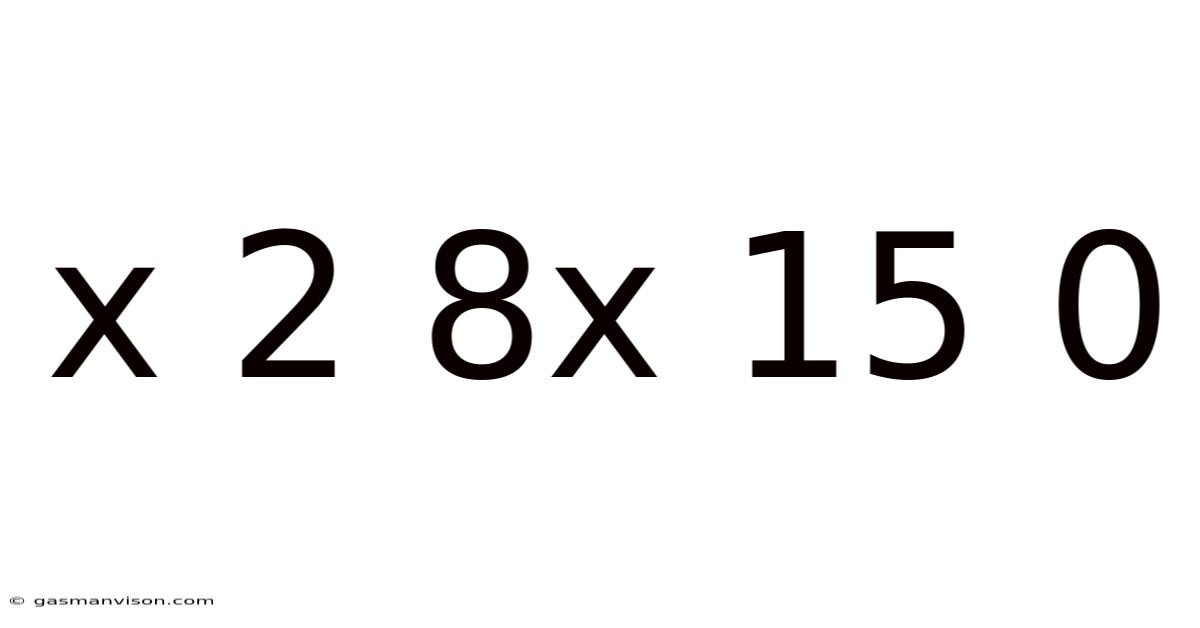
Table of Contents
Decoding the Mystery: x² + 8x + 15 = 0
This seemingly simple quadratic equation, x² + 8x + 15 = 0, holds within it the potential for a deep dive into the world of algebra, revealing fundamental concepts and problem-solving techniques applicable to numerous mathematical fields. This article will not only solve the equation but will explore various methods, providing a comprehensive understanding of quadratic equations and their significance. We will also delve into the practical applications of these equations in real-world scenarios.
Understanding Quadratic Equations
Before we tackle x² + 8x + 15 = 0, let's establish a foundational understanding of quadratic equations. A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (in this case, x) is 2. The general form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0 (if a were 0, it wouldn't be a quadratic equation).
The solutions to a quadratic equation, also known as its roots or zeros, represent the x-values where the corresponding quadratic function (y = ax² + bx + c) intersects the x-axis. These roots can be real or complex numbers. Understanding the nature of these roots is crucial in interpreting the equation's meaning within a given context.
Method 1: Factoring
Factoring is perhaps the most straightforward method for solving quadratic equations, particularly when the equation is easily factorable. The goal is to rewrite the equation as a product of two linear expressions. Let's apply this to our equation: x² + 8x + 15 = 0.
We need to find two numbers that add up to 8 (the coefficient of x) and multiply to 15 (the constant term). Those numbers are 3 and 5. Therefore, we can factor the equation as follows:
(x + 3)(x + 5) = 0
This equation is satisfied if either (x + 3) = 0 or (x + 5) = 0. Solving these linear equations gives us the two roots:
x = -3 and x = -5
Therefore, the solutions to the quadratic equation x² + 8x + 15 = 0 are x = -3 and x = -5.
Method 2: Quadratic Formula
The quadratic formula is a more general method applicable to all quadratic equations, even those that are difficult or impossible to factor easily. The formula is derived from completing the square and provides a direct way to calculate the roots.
The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
For our equation, x² + 8x + 15 = 0, we have a = 1, b = 8, and c = 15. Substituting these values into the quadratic formula, we get:
x = [-8 ± √(8² - 4 * 1 * 15)] / (2 * 1)
x = [-8 ± √(64 - 60)] / 2
x = [-8 ± √4] / 2
x = [-8 ± 2] / 2
This gives us two solutions:
x = (-8 + 2) / 2 = -3
x = (-8 - 2) / 2 = -5
Again, we arrive at the same solutions: x = -3 and x = -5. This confirms the accuracy of our factoring method.
Method 3: Completing the Square
Completing the square is another algebraic technique used to solve quadratic equations. It involves manipulating the equation to create a perfect square trinomial, which can then be easily factored.
Let's apply this method to x² + 8x + 15 = 0:
-
Move the constant term to the right side: x² + 8x = -15
-
Take half of the coefficient of x (which is 8), square it (8/2 = 4, 4² = 16), and add it to both sides: x² + 8x + 16 = -15 + 16
-
Factor the left side as a perfect square trinomial: (x + 4)² = 1
-
Take the square root of both sides: x + 4 = ±√1
-
Solve for x: x = -4 ± 1
This yields the two solutions:
x = -4 + 1 = -3
x = -4 - 1 = -5
Once more, we obtain the solutions x = -3 and x = -5. This demonstrates the consistency and reliability of different algebraic approaches.
Interpreting the Results and Graphical Representation
The solutions x = -3 and x = -5 represent the x-intercepts of the parabola defined by the quadratic function y = x² + 8x + 15. Graphically, this means the parabola intersects the x-axis at the points (-3, 0) and (-5, 0). The parabola opens upwards because the coefficient of x² (which is 1) is positive. Understanding this graphical representation helps visualize the relationship between the equation and its solutions.
Real-World Applications
Quadratic equations are not merely abstract mathematical concepts; they have numerous practical applications in various fields:
-
Physics: Calculating projectile motion, determining the trajectory of an object under gravity, and analyzing oscillations.
-
Engineering: Designing structures, optimizing shapes for strength and stability, and solving problems related to fluid dynamics.
-
Economics: Modeling supply and demand, determining optimal production levels, and analyzing market equilibrium.
-
Computer Graphics: Creating curved shapes and surfaces, simulating realistic movements, and generating intricate visual effects.
-
Finance: Calculating compound interest, determining investment growth, and modeling financial risk.
Further Exploration: Discriminant and Nature of Roots
The discriminant, denoted by Δ (delta), is the expression inside the square root in the quadratic formula (b² - 4ac). The discriminant determines the nature of the roots of a quadratic equation:
- Δ > 0: The equation has two distinct real roots.
- Δ = 0: The equation has one real root (a repeated root).
- Δ < 0: The equation has two complex conjugate roots.
For our equation, x² + 8x + 15 = 0, the discriminant is:
Δ = 8² - 4 * 1 * 15 = 4
Since Δ > 0, we have two distinct real roots, which are -3 and -5, as we have already calculated.
Conclusion
Solving the quadratic equation x² + 8x + 15 = 0 provides a stepping stone to understanding a fundamental concept in algebra. We have explored various methods—factoring, the quadratic formula, and completing the square—demonstrating the versatility and robustness of these techniques. The ability to solve quadratic equations is not just an academic exercise; it's a crucial skill with far-reaching applications in diverse fields, highlighting the practical relevance of mathematical concepts in the real world. The exploration of the discriminant further enhances our comprehension of the characteristics and behavior of quadratic equations. Mastering these concepts provides a strong foundation for tackling more complex mathematical problems in the future.
Latest Posts
Latest Posts
-
Does Hcn Have Resonance Structures
Sep 20, 2025
-
To Corroborate Information Is To
Sep 20, 2025
-
20 Percent Off 40 Dollars
Sep 20, 2025
-
Which Are Characteristics Of Theories
Sep 20, 2025
-
The First Mesoamerican Civilizations Began
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about X 2 8x 15 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.