X 2 9x 2 0
gasmanvison
Sep 07, 2025 · 5 min read
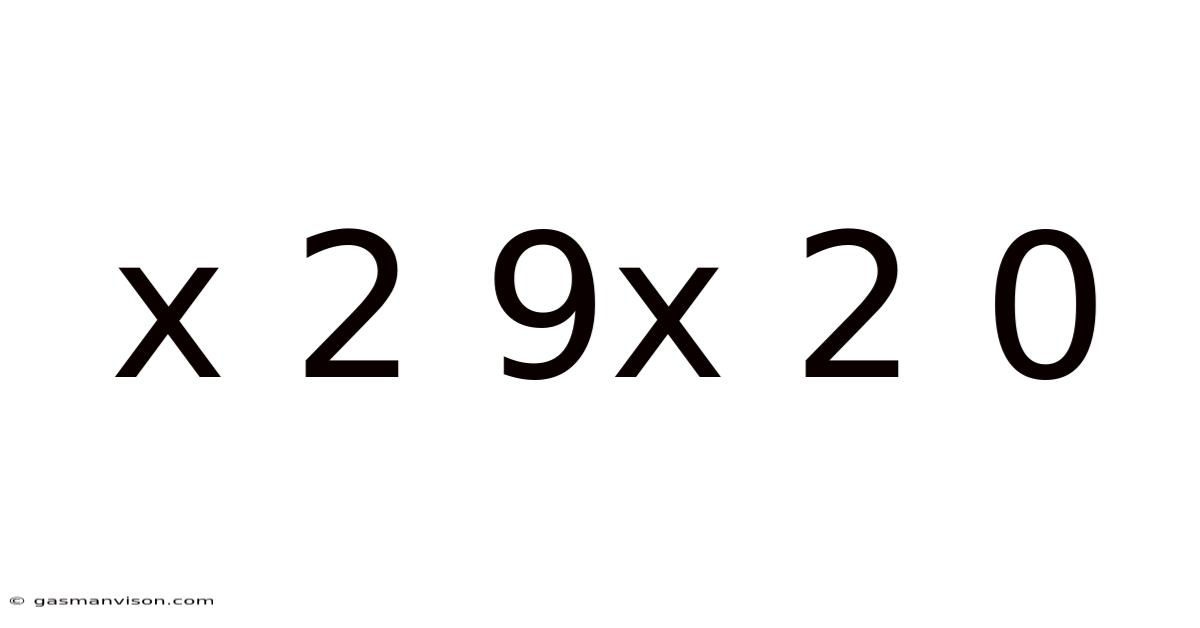
Table of Contents
Deconstructing x² + 9x² = 0: A Deep Dive into Quadratic Equations and Their Solutions
This article explores the seemingly simple quadratic equation x² + 9x² = 0, delving into its solution methods, the underlying mathematical principles, and its broader relevance within the field of algebra. While the equation itself might appear straightforward, its analysis provides a valuable foundation for understanding more complex quadratic problems and related concepts. This exploration will cover various solution techniques, discuss the nature of quadratic equations, and highlight the importance of simplifying expressions before solving.
Meta Description: This article provides a comprehensive guide to solving the quadratic equation x² + 9x² = 0, covering various solution methods, explaining the underlying mathematical principles, and exploring its broader applications in algebra. Learn about simplifying equations, factoring, and the significance of understanding quadratic forms.
Understanding the Equation: A First Glance
The equation x² + 9x² = 0 presents a classic example of a quadratic equation, albeit a particularly simple one. A quadratic equation is defined by its highest power of the variable (x in this case), which is 2. The general form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0. In our equation, we have a simplified form where the 'b' and 'c' coefficients are both zero. This simplifies the process of finding a solution, but the fundamental principles remain the same.
Simplifying the Equation: The First Step to Success
Before diving into solution methods, the initial and crucial step is to simplify the equation. Notice that both terms on the left-hand side contain x². This allows us to combine them:
x² + 9x² = 10x²
Therefore, the simplified equation becomes:
10x² = 0
Solving the Equation: Multiple Approaches
Now, let's explore several methods to solve the simplified equation 10x² = 0. Each method offers a slightly different perspective on the underlying mathematical principles.
Method 1: Dividing by the Coefficient
The most straightforward approach involves dividing both sides of the equation by the coefficient of x², which is 10:
10x² / 10 = 0 / 10
This simplifies to:
x² = 0
Taking the square root of both sides:
√x² = √0
This gives us the solution:
x = 0
Method 2: Factoring the Equation
Another powerful method is factoring. While seemingly unnecessary in this simple case, it illustrates a technique crucial for solving more complex quadratic equations. We can factor out x² from the simplified equation:
10x² = x²(10) = 0
This equation is satisfied if either x² = 0 or 10 = 0. Since 10 cannot equal zero, the only solution is:
x² = 0 => x = 0
Method 3: The Quadratic Formula (Though Unnecessary Here)
The quadratic formula is a general method for solving quadratic equations of the form ax² + bx + c = 0. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
In our simplified equation (10x² = 0), a = 10, b = 0, and c = 0. Substituting these values into the quadratic formula:
x = [-0 ± √(0² - 4 * 10 * 0)] / (2 * 10)
x = 0 / 20
x = 0
While the quadratic formula works, it's an overkill for such a simple equation. The previous methods are far more efficient.
The Nature of Quadratic Equations and Their Solutions
Quadratic equations, in their general form, can have up to two distinct real solutions, one repeated real solution, or two complex conjugate solutions. The discriminant (b² - 4ac) determines the nature of the solutions:
- b² - 4ac > 0: Two distinct real solutions
- b² - 4ac = 0: One repeated real solution (a double root)
- b² - 4ac < 0: Two complex conjugate solutions
In our equation, x² + 9x² = 0, the discriminant is 0 (since a = 10, b = 0, c = 0), indicating a single repeated real solution, which is x = 0.
Applications and Further Exploration
While the equation x² + 9x² = 0 might seem trivial, understanding its solution provides a strong base for tackling more complex quadratic equations. This simple equation highlights the importance of:
- Equation Simplification: Before attempting to solve any equation, always simplify it to its most basic form. This often makes the solution process significantly easier.
- Multiple Solution Methods: Familiarizing yourself with multiple solution methods (factoring, quadratic formula, etc.) allows you to choose the most efficient approach for a given problem.
- Understanding the Discriminant: The discriminant helps predict the nature of the solutions without actually solving the equation. This is useful in various applications, including graphing quadratic functions.
Furthermore, quadratic equations have numerous applications in various fields, including:
- Physics: Calculating trajectories of projectiles, analyzing oscillations, and modeling simple harmonic motion.
- Engineering: Designing structures, optimizing systems, and solving problems related to energy and force.
- Economics: Modeling supply and demand, analyzing market trends, and optimizing production.
- Computer Science: Algorithms, optimization problems, and computer graphics.
Expanding the Concept: More Complex Quadratic Equations
To solidify your understanding, let's consider a slightly more complex example:
2x² - 5x + 2 = 0
This equation requires a more involved solution process. We can solve it using factoring:
(2x - 1)(x - 2) = 0
This gives us two solutions:
2x - 1 = 0 => x = 1/2 x - 2 = 0 => x = 2
Alternatively, we can use the quadratic formula:
a = 2, b = -5, c = 2
x = [5 ± √((-5)² - 4 * 2 * 2)] / (2 * 2)
x = [5 ± √9] / 4
x = [5 ± 3] / 4
This yields the same solutions: x = 1/2 and x = 2.
Conclusion: Mastering the Fundamentals
The seemingly simple equation x² + 9x² = 0, while easily solvable, offers a valuable gateway to understanding the broader world of quadratic equations. By mastering the fundamental techniques and concepts discussed in this article, you'll be well-equipped to tackle more complex quadratic problems and appreciate their widespread applications across various fields. Remember to always simplify, explore multiple solution methods, and understand the significance of the discriminant in determining the nature of the solutions. This foundational knowledge will serve as a cornerstone for your further exploration of algebra and related mathematical disciplines.
Latest Posts
Latest Posts
-
5 To The Fifth Power
Sep 07, 2025
-
28 Grams In A Ounce
Sep 07, 2025
-
Number Of Protons In Xenon
Sep 07, 2025
-
Bad Things Andrew Carnegie Did
Sep 07, 2025
-
How To Determine Theoretical Yield
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about X 2 9x 2 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.