X 2 Y 2 16
gasmanvison
Sep 14, 2025 · 5 min read
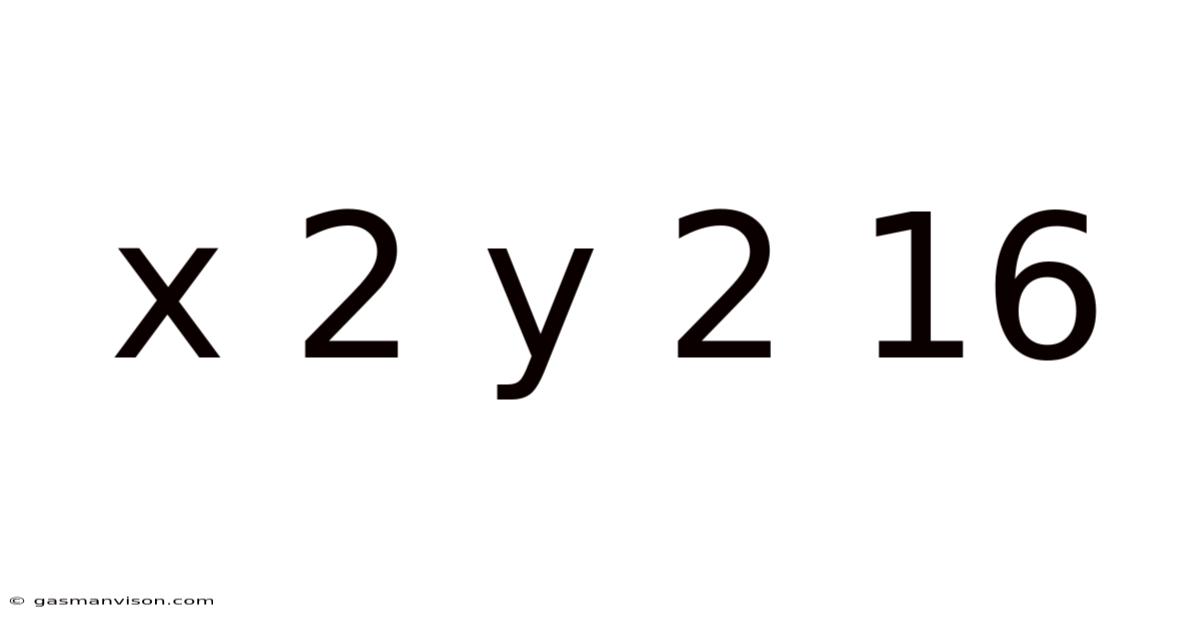
Table of Contents
Decoding the Enigma: Exploring the Mathematical Landscape of x² + y² = 16
This article delves into the fascinating mathematical equation x² + y² = 16, exploring its geometric representation, algebraic solutions, and the broader mathematical concepts it illuminates. We'll move beyond a simple solution and uncover the rich tapestry of mathematical ideas woven into this seemingly straightforward expression. Understanding this equation provides a foundation for comprehending more complex concepts in algebra, geometry, and even calculus.
What does x² + y² = 16 represent?
At its core, x² + y² = 16 represents a circle in a two-dimensional Cartesian coordinate system. The equation is a specific instance of the general equation for a circle centered at the origin (0,0): x² + y² = r², where 'r' represents the radius of the circle. In our case, r² = 16, meaning the radius of the circle is √16 = 4 units. This simple equation elegantly describes a perfectly symmetrical shape with all points equidistant from the center. This geometric interpretation is crucial for understanding its solutions and applications.
Algebraic Solutions and Their Significance:
Solving x² + y² = 16 algebraically involves finding pairs of (x, y) coordinates that satisfy the equation. While there's no single "solution," there's an infinite number of solutions representing all the points on the circle. We can find specific solutions by choosing a value for x (or y) and solving for the corresponding value of y (or x).
For instance:
- If x = 0: Then y² = 16, giving y = ±4. This yields the points (0, 4) and (0, -4).
- If y = 0: Then x² = 16, giving x = ±4. This yields the points (4, 0) and (-4, 0).
- If x = 2: Then 4 + y² = 16, so y² = 12, and y = ±√12 = ±2√3. This gives the points (2, 2√3) and (2, -2√3).
We can continue this process, generating an infinite set of (x, y) pairs. However, it's important to understand that these are just some of the solutions, not the complete set. The circle's continuous nature means there are infinitely many points along its circumference.
Parametric Representation: A More Elegant Approach
A more comprehensive approach to representing the solutions involves using parametric equations. This method uses a single parameter, typically denoted by 't', to define both x and y. For a circle centered at the origin with radius r, the parametric equations are:
- x = r * cos(t)
- y = r * sin(t)
In our case, r = 4, so the parametric equations for x² + y² = 16 are:
- x = 4 * cos(t)
- y = 4 * sin(t)
As 't' varies from 0 to 2π (a full circle), the equations generate all the points on the circle. This approach provides a more concise and elegant way to represent the infinite set of solutions. It's particularly useful in calculus and other advanced mathematical fields.
Exploring the Equation in Different Mathematical Contexts:
The equation x² + y² = 16 transcends simple algebraic solutions and geometric interpretations. Its significance expands into various mathematical branches:
1. Trigonometry: The equation directly relates to trigonometric identities. The parametric representation clearly highlights the connection between the circle and trigonometric functions (sine and cosine). This relationship is fundamental in trigonometry and its applications.
2. Calculus: The equation can be used to explore concepts like arc length, area, and differentiation. For instance, calculating the circumference of the circle involves integrating the arc length formula, demonstrating the interplay between geometry and calculus. Furthermore, the equation can be used to illustrate implicit differentiation techniques.
3. Complex Numbers: The equation can be expressed using complex numbers. If we let z = x + iy, where 'i' is the imaginary unit (√-1), then the equation can be rewritten as |z|² = 16, where |z| represents the modulus or magnitude of the complex number z. This perspective opens doors to understanding complex analysis and its applications.
4. Linear Algebra: The equation can be viewed in the context of vectors and matrices. Each point (x, y) can be represented as a vector, and the equation describes the set of all vectors with a magnitude (length) of 4.
5. Three-Dimensional Geometry: While the equation itself is two-dimensional, it can be extended to three dimensions to represent a cylinder. In this case, the equation becomes x² + y² = 16, with 'z' being unrestricted. This demonstrates how seemingly simple equations can be extended and interpreted in higher dimensions.
Applications and Real-World Relevance:
Beyond its theoretical significance, x² + y² = 16 finds practical applications in various fields:
- Physics: Circular motion, projectile motion, and wave phenomena often involve equations similar to x² + y² = 16. Understanding the equation helps model these physical phenomena.
- Engineering: The circle, represented by the equation, is crucial in designing gears, wheels, and other circular components in mechanical systems.
- Computer Graphics: The equation is fundamental in generating and manipulating circular shapes in computer graphics and animation.
- Mapping and Navigation: GPS systems and mapping applications rely on coordinate systems and circular representations to determine locations and distances.
Extending the Concept: Variations and Generalizations:
We can expand our understanding by exploring variations and generalizations of the equation:
- x² + y² = r²: This represents a circle with radius 'r', centered at the origin. Changing 'r' changes the size of the circle.
- (x - a)² + (y - b)² = r²: This represents a circle with radius 'r' and center at (a, b). This generalization allows for circles not centered at the origin.
- ax² + by² = c: This represents ellipses, which are stretched or compressed circles. The values of a, b, and c determine the shape and size of the ellipse. When a = b = 1, it simplifies back to our original circle equation.
Understanding these generalizations provides a deeper insight into conic sections and their properties.
Conclusion:
The seemingly simple equation x² + y² = 16 reveals a rich mathematical landscape, connecting algebra, geometry, trigonometry, calculus, and even complex numbers. Its geometric representation as a circle provides a visual anchor for understanding its solutions and applications. By exploring its various interpretations and extensions, we gain a deeper appreciation for the power and elegance of mathematical equations and their pervasive influence across diverse fields. This equation serves as a microcosm of mathematics itself, showing how seemingly simple concepts can lead to profound insights and applications in the world around us. The journey from a basic algebraic expression to a deeper understanding of circles, trigonometric functions, and their real-world relevance highlights the beauty and interconnectedness of mathematical principles. This exploration encourages further investigation into related mathematical concepts and strengthens the foundation for understanding more complex mathematical ideas.
Latest Posts
Latest Posts
-
Nitric Oxide Vs Nitrous Oxide
Sep 14, 2025
-
This Citation Is Missing The
Sep 14, 2025
-
Identity Vs Role Confusion Example
Sep 14, 2025
-
9 Gallons How Many Quarts
Sep 14, 2025
-
Why Are Coral Reefs Important
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about X 2 Y 2 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.